問題描述：

在一個2k×2k 個方格組成的棋盤中，有一個方格與其它不同，稱該方格為特殊方格，且稱該棋盤為一特殊棋盤。

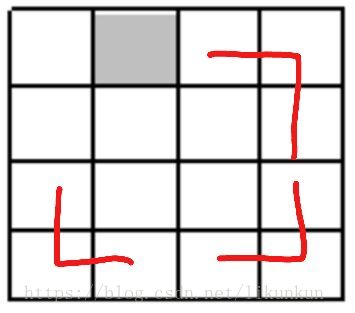
            k=2時的一種棋盤

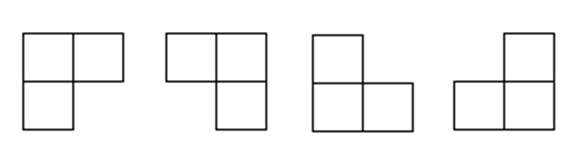
要求用下圖所示的4種L形態骨牌覆蓋給定的特殊棋盤。

限制條件：

（1）覆蓋給定特殊棋盤上除特殊方格以外的所有方格。

（2）任何2個L型骨牌不得重疊覆蓋。

解決思路：

• 特殊方格在棋盤中可能出現的位置有4^k種，因而有4^k種不同的棋盤。
• k>0時，可將2^k×2^k的棋盤劃分為4個2^（k-1）×2^（k-1）的子棋盤。
• 劃分後，這4個子棋盤中只有一個子棋盤包含該特殊方格。
• 將其餘3個子棋盤轉化為特殊棋盤，轉化方式：在三個子棋盤匯合處，設定為特殊方格。
• 因此，可以用一個L型骨牌覆蓋這3個較小棋盤的會合處，從而將原問題轉化為4個較小規模的棋盤覆蓋問題。
• 遞迴地使用這種劃分策略，直至將棋盤分割為1×1的子棋盤。

具體步驟：

    1、把整個棋盤劃分為左上、右上、左下、右下四塊，然後判斷特殊的方塊在哪一塊裡面。

    2、假如在左上這一塊區域裡面，我們就再把這塊區域劃分四塊，直到找到為止。

    3、其他沒有特殊方塊的區域，開始填充L形的牌。

    4、先把最周圍的方格填上L形牌。如下圖所示：

5、分割成4塊之後，沒有特殊方塊的那3塊區域只要如上圖填充完後，中間正好剩下一塊L形區域，如下圖。

時間複雜度分析：

設T(k)是覆蓋一個2k x 2k棋盤所需時間，T(k)滿足如下遞推式：

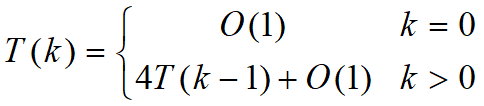
解：

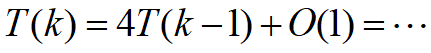
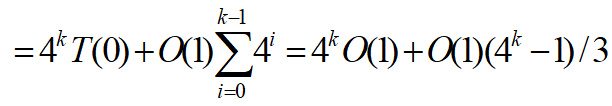
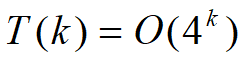
具體的實現程式碼（java實現）：

public class ChessProblem {
	
	int size;//容量
	int[][] board;//棋盤
	int specialROW;//特殊點橫座標
	int specialCOL;//特殊點縱座標
	int number = 0;//L形編號
	
	public ChessProblem(int specialRow, int specialCol, int size) {
		this.size = size;
		this.specialCOL = specialCOL;
		this.specialROW = specialROW;
		board = new int[size][size];
	}
	
	//specialROW   特殊點的行下標
	//specialCOL   特殊點的列下標
	//leftRow      矩陣的左邊起點行下標
	//leftCol      矩陣左邊起點的列下標
	//size         矩陣的寬或者高
	
 	public void setBoard(int specialROW, int specialCOL, int leftROW, int leftCOL, int size) {
		if (1 == size) {
			return;
		}
		
		int subSize = size / 2;
		number++;
		int n = number;//注意這裡一定要吧number存在當前的遞迴層次裡，否則進入下一層遞迴全域性變數會發生改變
		
		//假設特殊點在左上角區域
		if (specialROW < leftROW + subSize && specialCOL < leftCOL + subSize) {
			setBoard(specialROW, specialCOL, leftROW, leftCOL, subSize);
		}
		else {
			//不在左上角，設左上角矩陣的右下角就是特殊點（和別的一起放置L形）
			board[leftROW + subSize - 1][leftCOL + subSize - 1] = n;
			setBoard(leftROW + subSize - 1, leftCOL + subSize - 1, leftROW, leftCOL, subSize);
		}
		
		//假設特殊點在右上方
		if (specialROW < leftROW + subSize && specialCOL >= leftCOL + subSize) {
			setBoard(specialROW, specialCOL, leftROW, leftCOL + subSize, subSize);
		}
		else {
			//不在右上方，設右上方矩陣的左下角就是特殊點（和別的一起放置L形）
			board[leftROW + subSize -1][leftCOL + subSize] = n;
			setBoard(leftROW + subSize -1, leftCOL + subSize, leftROW, leftCOL + subSize, subSize);
		}
		
		//特殊點在左下方
		if (specialROW >= leftROW + subSize && specialCOL < leftCOL + subSize) {
			setBoard(specialROW, specialCOL, leftROW + subSize, leftCOL, subSize);
		}
		else {
			//不在左下方，設左下方矩陣的右上角就是特殊點（和別的一起放置L形）
			board[leftROW + subSize][leftCOL + subSize - 1] = n;
			setBoard(leftROW + subSize, leftCOL + subSize - 1, leftROW + subSize, leftCOL, subSize);
		}
 
		//特殊點在右下角
		if (specialROW >= leftROW + subSize && specialCOL >= leftCOL + subSize) {
			setBoard(specialROW, specialCOL, leftROW + subSize, leftCOL + subSize, subSize);
		}
		else {
			//不在右下角，設右下角矩陣的左上就是特殊點（和別的一起放置L形）
			board[leftROW + subSize][leftCOL + subSize] = n;
			setBoard(leftROW + subSize, leftCOL + subSize, leftROW + subSize, leftCOL + subSize, subSize);			
		}	
	}
	
 	
 	public void printBoard(int specialRow,int specialCol,int size) {
 		setBoard(specialRow, specialCol, 0, 0, size);
 		for (int i = 0; i < board.length; i++) {
			for (int j = 0; j < board.length; j++) {
				System.out.print(board[i][j] + " ");				
			}
			System.out.println();
		}
 	}
 	
 	
	public static void main(String[] args) {
		int N = 4;
		int specialRow = 0;
		int specialCol = 1;
		ChessProblem chessProblem = new ChessProblem(specialRow , specialCol , N);
		chessProblem.printBoard(specialRow, specialCol, N);
	}
}