作者：白寧超

2016年7月12日14:08:28

摘要：最早接觸馬爾可夫模型的定義源於吳軍先生《數學之美》一書，起初覺得深奧難懂且無什麼用場。直到學習自然語言處理時，才真正使用到隱馬爾可夫模型，並體會到此模型的妙用之處。馬爾可夫模型在處理序列分類時具體強大的功能，諸如解決：詞類標註、語音識別、句子切分、字素音位轉換、區域性句法剖析、語塊分析、命名實體識別、資訊抽取等。另外廣泛應用於自然科學、工程技術、生物科技、公用事業、通道編碼等多個領域。本文寫作思路如下：第一篇對馬爾可夫個人簡介和馬爾科夫鏈的介紹；第二篇介紹馬爾可夫鏈（顯馬爾可夫模型）和隱馬爾可夫模型以及隱馬爾可夫模型的三大問題（似然度、編碼、引數學習）；第三至五篇逐一介紹三大問題相關演算法：（向前演算法、維特比演算法、向前向後演算法

）；最後非常得益於馮志偉先生自然語言處理教程一書，馮老研究自然語言幾十餘載，在此領域別有建樹。

目錄

【自然語言處理：馬爾可夫模型（一）】：

馬爾可夫個人簡介

安德烈·馬爾可夫，俄羅斯人，物理-數學博士，聖彼得堡科學院院士，彼得堡數學學派的代表人物，以數論和概率論方面的工作著稱，他的主要著作有《概率演算》等。1878年，榮獲金質獎章，1905年被授予功勳教授稱號。馬爾可夫是彼得堡數學學派的代表人物。以數論和概率論方面的工作著稱。他的主要著作有《概率演算》等。在數論方面，他研究了連分數和二次不定式理論 ，解決了許多難題 。在概率論中，他發展了矩陣法，擴大了大數律和中心極限定理的應用範圍。馬爾可夫最重要的工作是在1906～1912年間，提出並研究了一種能用數學分析方法研究自然過程的一般圖式——馬爾可夫鏈。同時開創了對一種無後效性的隨機過程——馬爾可夫過程的研究。馬爾可夫經多次觀察試驗發現，一個系統的狀態轉換過程中第n次轉換獲得的狀態常取決於前一次（第（n-1）次）試驗的結果。馬爾可夫進行深入研究後指出：對於一個系統，由一個狀態轉至另一個狀態的轉換過程中，存在著轉移概率，並且這種轉移概率可以依據其緊接的前一種狀態推算出來，與該系統的原始狀態和此次轉移前的馬爾可夫過程無關。馬爾可夫鏈理論與方法在現代已經被廣泛應用於自然科學、工程技術和公用事業中。

1 演算法原理描述

維特比演算法解決：問題2（解碼問題）：給定一個觀察序列O和一個HMM λ=（A,B），找出最好的隱藏狀態序列Q。

解碼：使HMM這種包含隱藏變數的模型中，確定隱藏在某個觀察序列後面變數序列的工作，叫做解碼。

形式化描述：給定一個HMMλ=（A,B）和一個觀察序列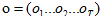 作為輸入，找出概率最大的狀態序列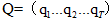就是解碼。

思想：使用前面演算法找到隱藏在觀察序列之後最好的狀態序列，對於每個可能的隱藏狀態序列，運用向前演算法選出觀察序列對隱藏序列的最大似然度的隱藏狀態序列，從而完成解碼工作，演算法複雜度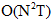，當狀態序列很大時，指數級增長，計算量過大，由此採用一種動態規劃演算法降低演算法複雜度：維特比演算法。

2 維特比演算法例項分析

例子：通過吃冰淇淋數量（觀察序列狀態）計算隱藏狀態空間的最佳路徑（維特比網格）如下:

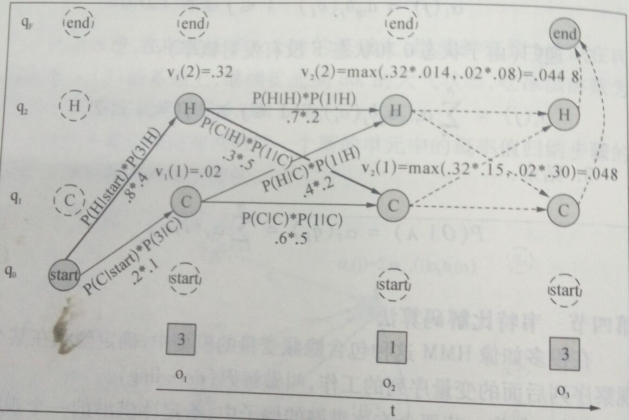
其中：

圓圈：隱藏狀態            方框：觀察狀態 
虛線圓圈：非法轉移      虛線：計算路徑  
q：隱藏空間狀態              o：觀察時間序列狀態

 ：在時間步t的觀察狀態下，隱藏狀態j的概率。

Viterbi演算法思想：按照觀察序列由左向右順序，每個表示自動機λ，HMM在看了頭t個觀察並通過了概率最大的狀態序列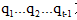 之後，在狀態j的概率，每個 的值遞迴計算，並找出最大路徑。

Viterbi演算法形式化描述：每一個單元表示如下概率：

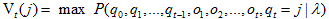
V的計算公式如下：

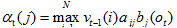
在時刻t-1的時候使用擴充前面路徑的方法計算維特比概率，計算時，把下面3個因素相乘：

案例分析：

給定一個HMMλ=（A,B），HMM把最大似然度指派給觀察序列，演算法返回狀態路徑，從而找到最優的隱藏狀態序列。上圖是小明夏天吃冰淇淋‘3 1 3’，據此使用Viterbi演算法推斷最可能出現的天氣狀態（天氣的熱|冷）。

1）計算時間步1的維特比概率

計算時間步t=1和狀態1的概率：

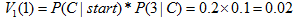
路徑：start--C

計算時間步t=1和狀態2的概率：

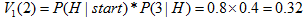
路徑：start—H  較大

2）計算時間步2的維特比概率，在（1） 基礎計算

計算時間步t=2和狀態1的概率：

路徑:start—H—C   較大

計算時間步t=2和狀態2的概率：

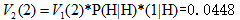
路徑：start—H--H

3）計算時間步3的維特比概率，在（2） 基礎計算

計算時間步t=3和狀態1的概率：

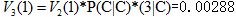
路徑:start—H—C —C

計算時間步t=3和狀態2的概率：

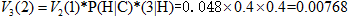
路徑：start—H—C—H  較大

4）維特比反向追蹤路徑

路徑為：start—H—C---H

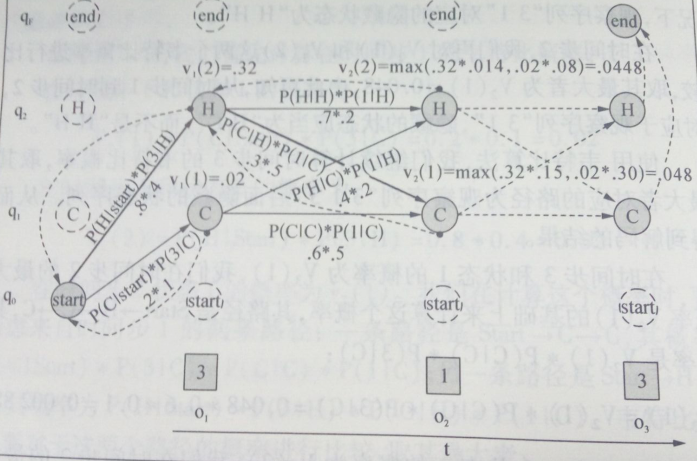
綜上所述可知：利用Viterbi演算法我們知道小明夏天某天吃冰淇淋的觀察值（3 1 3）推斷出天氣為（熱 冷 熱）。這也符合事實，天熱吃3根，天冷吃一根。

維特比演算法與向前演算法的區別：

（1）    維特比演算法要在前面路徑的概率中選擇最大值，而向前演算法則計算其總和，除此之外，維特比演算法和向前演算法一樣。

（2）    維特比演算法有反向指標，尋找隱藏狀態路徑，而向前演算法沒有反向指標。

3 HMM和維特比演算法解決隨機詞類標註問題

上面例子根據小明吃冰淇淋成功推斷出天氣事件，但是讀者不免意猶未盡，那麼下面利用同樣方法進行詞類標註。在隨機詞類標註演算法中，單詞是觀察序列，相當於冰淇淋的數量。詞類標記是隱藏狀態，相當於天氣的熱冷。因此可以進行隨機詞類標註如下：

對於一個給定的句子或者單詞序列，我們使用HMM詞類標註演算法來選擇使用下面公式為最大值標記序列：

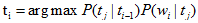
在進行詞類標註時，句子“Secretariat is expected to race tomorrow”中的race是一個動詞VB或者名詞NN，它可以標註VB也可以標註NN，我們利用Viterbi演算法解決：

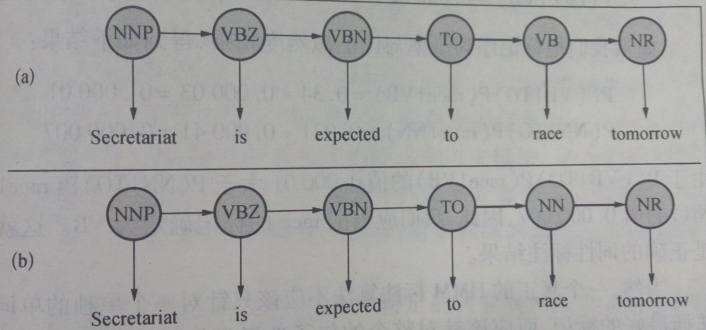
根據HMM標註演算法的公式可知，選擇概率比較大的一個作為race的標記。P(VB|TO)*P(race|VB)  和P(NN|TO)*P(race|NN) 兩者最大值即race的標記。

假設轉移概率已知為：

P(NN|TO)=0.021

P(VB|TO)=0.34

假設詞彙的發射概率即似然度也是知道的：

P(race|NN)=0.00041

P(race|VB)=0.00003

我們把標記序列概率和詞彙發射概率相乘得到以下結果：

P(VB|TO)*P(race|VB) = 0.034*0.00003=0.00001

P(NN|TO)*P(race|NN) =0.021*0.00041=0.000007

因此，我們把race的標記確定為VB，這就是正確的詞類標記結果，本質上採用統計模型的方法。當然真正使用時，我們根據需求對整個句子或者整段話以至於整篇文章進行標註，原理是一樣的。

4 維特比演算法描述

Viterbi演算法定義：

5 利用Viterbi演算法的中文句法標註

1 對文字資料清洗的預處理操作。程式碼略

2 對清洗後的文字，採用有監督方法對古文獻BIO標記（B表示句子開始I表示句子中間O表示句子結尾）程式碼略

3 統計文字的轉移矩陣B。 程式碼略

4 統計文字的發射矩陣A。 程式碼略

5 維特比解碼演算法找出觀察序列O的最後的隱藏狀態序列Q

5.1 隱馬爾可夫模型中維特比解碼演算法序列標註

String observationStr="病有發熱惡寒者；發於陽也，無熱惡寒者；發於陰也。";//觀察序列
String[] states={"B","I","O"};//狀態序列
double start_probability=0.3333;//初始狀態概率
String str="書名：傷寒論。作者：張仲景。朝代：東漢。";
String stateStr=MethodUilt.Vitrerbi(str, start_probability, Amatrixpath, Bmatrixpath);//隱藏狀態序列，即隱含馬爾科夫模型的詞類標註
System.out.println("觀察序列：\t"+str.replaceAll("", "\t")+"\n標註序列：\t\t"+stateStr);
		

 5.2 針對馬爾科夫模型中第二個問題，採用維特比演算法進行句子標註，其中主要還是動態規劃思想

	/**
	 * 針對馬爾科夫模型中第二個問題，採用維特比演算法進行句子標註，其中主要還是動態規劃思想
	 * @param observationStr 觀察序列
	 * @param states         狀態序列
	 * @param start_probability  初始化狀態,即π
	 * @param Amatrixpath    發射矩陣路徑
	 * @param Bmatrixpath    轉移矩陣路徑
	 * start_probability, transititon_probability, emission_probability
	 * @return
	 */
	public static String Vitrerbi(String observationStr,double start_probability,String Amatrixpath,String Bmatrixpath){
		//將觀察序列切詞儲存在數組裡面
		String[] ObserArr=observationStr.split("");
		//將發射矩陣放入陣列中
		String[] emissionArrs=HeplerUilt.readStrFile(Amatrixpath, "\n").split("\n");//文字中發射矩陣逐次切割放於一位陣列中
		Map<String,BIOEntity> countMap=new HashMap<String,BIOEntity>();//例項化map，儲存：詞+實體（二維陣列）
		for(int i=0;i<emissionArrs.length;i++){
			String[] rowdata = emissionArrs[i].split("\t");
			countMap.put(rowdata[0], new BIOEntity(rowdata[0],Double.parseDouble(rowdata[1]), Double.parseDouble(rowdata[2]), Double.parseDouble(rowdata[3])));
		}
		//轉移概率矩陣放入陣列中
		String[] transititonArr=HeplerUilt.readStrFile(Bmatrixpath, "\t").split("\t");
		double[][] transArr=new double[3][3];//存放轉移矩陣
		int k=0;
		for(int i=0;i<transArr.length;i++){
			for(int j=0;j<transArr[i].length;j++){
				transArr[i][j]=Double.parseDouble(transititonArr[k]);
				k++;
			}
		}
		//隱含的標註序列
		String stateStr="";
		double V=0;//每步V*P(q_i|q_i-1)*P(w|q_i)
		List list = new LinkedList();//存放路徑
		//初始狀態V的值
		String tarWord=ObserArr[1];//首個字母
		for(Map.Entry<String, BIOEntity> entry : countMap.entrySet()){
			if(entry.getKey().equals(tarWord)){
				double emission_probability=HeplerUilt.getMax(entry.getValue().getXb(), entry.getValue().getXi(), entry.getValue().getXo());
				String prior=HeplerUilt.compareMark(entry.getValue().getXb(), entry.getValue().getXi(), entry.getValue().getXo());
				list.add(prior);
				V=start_probability*emission_probability;
				//System.out.println(tarWord+":"+start_probability+":"+emission_probability+":"+prior+":"+HeplerUilt.DecFormat(4,V));
			}
		}
		//觀察序列O，第二個狀態到結束
		for(int i=2;i<ObserArr.length;i++){//由初始狀態生成V，接著後面遍歷觀察序列進行
			for(Map.Entry<String, BIOEntity> entry : countMap.entrySet()){
				String q=list.get(list.size()-1).toString();//獲取前一個標註
				if(entry.getKey().equals(ObserArr[i])){     //獲取觀察序列的發射概率
					double max_probability=HeplerUilt.getMax(entry.getValue().getXb(), entry.getValue().getXi(), entry.getValue().getXo());//得到最大發射概率值
					double transititon_probability=HeplerUilt.getMaxTrans(q,transArr);                                                     //獲取最大的轉移概率
					String prior=HeplerUilt.compareMark(entry.getValue().getXb(), entry.getValue().getXi(), entry.getValue().getXo());//得到最大發射概率的標註
					list.add(prior);//將最大發射概率進行儲存
					V=V*max_probability*transititon_probability;//得到下一步的V值
					//測試資料
					//System.out.println(ObserArr[i]+":"+max_probability+":"+transititon_probability+":"+prior+":"+HeplerUilt.DecFormat(4,V));
				}
			}
		}
		//System.out.println(observationStr.length()+":"+list.size());
		for(int i=0;i<list.size();i++){
			stateStr+=list.get(i)+"\t";//記錄路徑
		}
		return stateStr;
	}
	//單元測試
	public static void main(String[] args) {
		//維特比解碼演算法找出觀察序列O的最後的隱藏狀態序列Q
				System.out.println("***************************隱馬爾可夫模型中維特比解碼演算法序列標註****************************");
				String observationStr="病有發熱惡寒者；發於陽也，無熱惡寒者；發於陰也。";//觀察序列
				String str="書名：傷寒論。作者：張仲景。朝代：東漢。";
				String stateStr=MethodUilt.Vitrerbi(str, 0.3333, "./targetFile/Amatrix.txt", "./targetFile/Bmatrix.txt");//隱藏狀態序列，即隱含馬爾科夫模型的詞類標註
				System.out.println("觀察序列：\t"+str.replaceAll("", "\t")+"\n標註序列：\t\t"+stateStr);
	}

 6 實驗結果：

3 參考文獻

【1】統計自然語言處理基礎  Christopher.Manning等 著    宛春法等 譯

【2】自然語言處理簡明教程  馮志偉 著

【3】數學之美  吳軍 著

【4】Viterbi演算法分析文章  王亞強

宣告：關於此文各個篇章，本人採取梳理扼要，順暢通明的寫作手法。一則參照相關資料二則根據自己理解進行梳理。避免冗雜不清，每篇文章讀者可理清核心知識，再找相關文獻系統閱讀。另外，要學會舉一反三，不要死盯著定義或者某個例子不放。諸如：此文章例子冰淇淋數量（觀察值）與天氣冷熱（隱藏值）例子，讀者不免問道此有何用？我們將冰淇淋數量換成中文文字或者語音（觀察序列），將天氣冷熱換成英文文字或者語音文字（隱藏序列）。把這個問題解決了不就是解決了文字翻譯、語音識別、自然語言理解等等。解決了自然語言的識別和理解，再應用到現在機器人或者其他裝置中，不就達到實用和聯絡現實生活的目的了？