一、背景

        本人在閱讀大神文章《Attention is all you need》的過程中，遇到了有關attention方面的內容，尤其是對於self-attention方面的內容饒有興趣，於是做了許多調查，下面是我的一些總結。

二、基本知識

       1、Attention Mechanism

           本文主要講解Self_attention方面的內容，這方面的知識是建立在attention機制之上的，因此若讀者不瞭解attention mechanism的話，希望你們能去略微瞭解一下。本人也將在這裡稍微的解釋一下。

           對於encoder-decoder模型，decoder的輸入包括（注意這裡是包括）encoder的輸出。但是根據常識來講，某一個輸出並不需要所有encoder資訊，而是只需要部分資訊。這句話就是attention的精髓所在。怎麼理解這句話呢？舉個例子來說：假如我們正在做機器翻譯，將“I am a student”翻譯成中文“我是一個學生”。根據encoder-decoder模型，在輸出“學生”時，我們用到了“我”“是”“一個”以及encoder的輸出。但事實上，我們或許並不需要“I am a ”這些無關緊要的資訊，而僅僅只需要“student”這個詞的資訊就可以輸出“學生”（或者說“I am a”這些資訊沒有“student”重要）。這個時候就需要用到attention機制來分別為“I”、“am”、“a”、“student”賦一個權值了。例如分別給“I am a”賦值為0.1，給“student”賦值剩下的0.7，顯然這時student的重要性就體現出來了。具體怎麼操作，我這裡就不在講了。

       2、self-attention

           self-attention顯然是attentio機制的一種。上面所講的attention是輸入對輸出的權重，例如在上文中，是I am a student 對學生的權重。self-attention則是自己對自己的權重，例如I am a student分別對am的權重、對student的權重。之所以這樣做，是為了充分考慮句子之間不同詞語之間的語義及語法聯絡。

           那麼這個權值應該怎麼計算呢？我在別處看到的圖片以及我自己的理解如下：

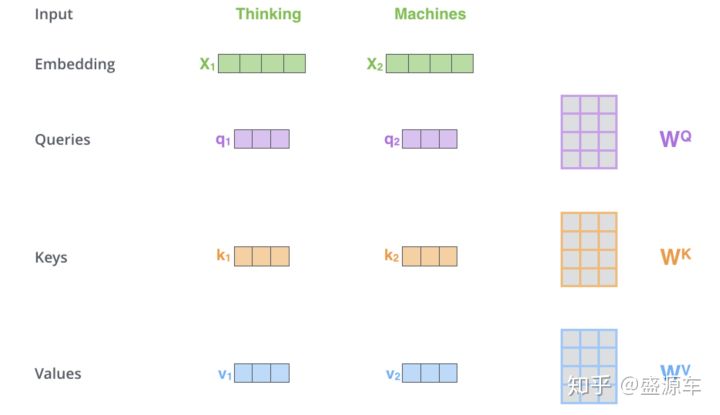
註釋：q\k\v分別對應attention機制中的Q\K\V，它們是通過輸入詞向量分別和W(Q)、W(K)、W(V)做乘積得到的。其目的主要是計算權值。

註釋：q與k做點乘、然後歸一化，就得到權值（乘積越大，相似度越高，權值越高）。得到的兩個權值分別與v相乘後，再相加就是輸出。同理就可以得到另一個單詞的輸出。

以上是一個單詞一個單詞的輸出，如果寫成矩陣形式就是Q*K，得到的矩陣歸一化直接得到權值。