c#使用委託實現辛普森法求多個函式的定積分
用辛普生法對幾個不同的被積函式求指定區間的定積分。被積函式為f(x),積分割槽間[a,b]被等分為n=2k份,每份步長為h=(b-a)/n,則積分值為:S≈h((f(a)+f(b))/2 +f(a+h)+…+f(a+(n-1)h))。
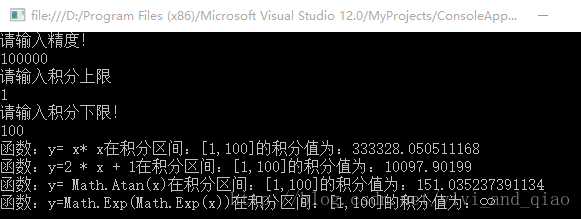
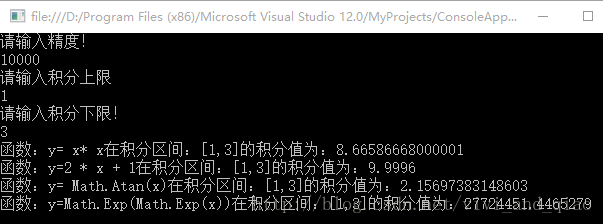
執行結果:
//辛普森法求積分
copyright vivi_and_qiao 李偉
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace 辛普森法求積分
{
delegate 相關推薦
c#使用委託實現辛普森法求多個函式的定積分
用辛普生法對幾個不同的被積函式求指定區間的定積分。被積函式為f(x),積分割槽間[a,b]被等分為n=2k份,每份步長為h=(b-a)/n,則積分值為:S≈h((f(a)+f(b))/2 +f(a+h)+…+f(a+(n-1)h))。 執行結果:
HDU 1724 ——————自適應辛普森法
Ellipse Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 2916 Accepted Submission(s): 133
洛谷 4525 && 洛谷 4526 【模板】自適應辛普森法
題目:https://www.luogu.org/problemnew/show/P4525 https://www.luogu.org/problemnew/show/P4526 參考:https://blog.csdn.net/VictoryCzt/article/details/8066011
自適應辛普森法
fin play lock sla a* printf max pso spa Simpson公式 設\(f(x)\)為原函數,$g(x)=Ax2+Bx+C $ 為擬合後的函數,則有: \[ \int_{a}^{b}f(x)dx \approx \int_{a}^{b}Ax
HDU1724-辛普森積分公式法求橢圓面積
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submissio
hdu1724 自適應辛普森積分 求面積 定積分
#include <iostream> #include <cstdio> #include <cstring> #include <cstdlib> #
辛普森積分法的學習
微積分是許多學科的基礎,在程式設計方面也有很大的作用,程式裡寫積分很多時候是用梯形法,今天學了一種叫辛普森積分的方法,感覺很好用只不過辛普森積分法在區間較大時誤差比較大,所以一般用二分減小區間大小以獲得更加精確的結果。現在以求兩個圓柱體相交部分的體積為例來學習辛普森積分:給
C語言實現粒子群算法(PSO)二
計算 default img 第一個元素 1.4 best 實驗 atl 說過 上一回說了基本粒子群算法的實現,並且給出了C語言代碼。這一篇主要講解影響粒子群算法的一個重要參數---w。我們已經說過粒子群算法的核心的兩個公式為: Vid(k+1)=w*Vid(k)+c1*r
C語言實現粒子群算法(PSO)一
mat 遺傳 基於 [1] 沒有 實驗 規模 直觀 解決 最近在溫習C語言,看的書是《C primer Plus》,忽然想起來以前在參加數學建模的時候,用過的一些智能算法,比如遺傳算法、粒子群算法、蟻群算法等等。當時是使用MATLAB來實現的,而且有些MATLAB自帶了工具
[待完善]關於辛普森公式的一點想法
16px 意思 onclick 自己 很大的 play 更多 ble turn [吐槽] 嗯一開始接觸到這個東西其實是因為某道凸包的題目好像可以用這個奇妙的方法來算 但其實了解也不是很深,只是覺得這個東西十分有意思, 所以先稍微寫一下自己的想法,了解更多之
Ellipse HDU - 1724(自適應辛普森積分)
img display 一個 blank c++ can 過程 遞歸 for Ellipse HDU - 1724 emmm...快比賽了先補幾個模板~ 自適應辛普森積分 1 #include <bits/stdc++.h> 2 using
【自適應辛普森積分】hdu1724 Ellipse
nts sin -s res a* max this 技術 eight Ellipse Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Subm
並不對勁的辛普森積分
bzoj 什麽 ++ cond script first 不用 bubuko alt 並不會計算幾何的並不對勁的人想必是非常之菜的。 很對勁的太刀流在這裏-> 辛普森積分本身是把一段函數f(x)當成二次函數算,用(f(l)+4*f((l+r)/2)+f(r))*(r-
[BZOJ1502]月下檸檬樹(自適應辛普森積分)
成了 typedef 高度 i++ ble 4.0 技術 https SQ 1502: [NOI2005]月下檸檬樹 Time Limit: 5 Sec Memory Limit: 64 MBSubmit: 1387 Solved: 739[Submit][Sta
辛普森積分
urn 計算幾何 include sca pre 每次 cst scanf rac 引例 計算積分:\[\int_{L}^{R} \frac{cx+d}{ax+b} dx\] 題解 其實可以直接求導然後做,然而太弱根本推不出來. 於是就可以使用自適應辛普森積分。 辛普森(S
【BZOJ2178】圓的面積並(辛普森積分)
lse double truct += ref bzoj2178 .com spa namespace 【BZOJ2178】圓的面積並(辛普森積分) 題面 BZOJ 權限題 題解 把\(f(x)\)設為\(x\)和所有圓交的線段的並的和。 然後直接上自適應辛普森積分。 我精
辛普森公式(理論+程式碼)
數學分析中的泰勒公式告訴我們,對任何函式,我們都可以用多項式函式去逼近它的函式值,且對於解析性質很好的函式(例如任意階可導+任意階導函式有界),我們可以將誤差縮小到任意小。 其中 那麼,我們在求解析式複雜或者可能無法用初等函式表示原函式的積分問題時,能否也可以用多項式函式來代替呢? 辛普
自適應辛普森公式
自適應辛普森公式 時間複雜度O(能過) double f(double x){ return x*x+sqrt(x); //積分函式 } double simpson(double a,double b){ double c=(a+b)/2.0; retu
複合梯形公式、複合辛普森公式 matlab
1. 用1階至4階Newton-Cotes公式計算積分 &n
數值積分Python(辛普森公式,Cotes公式)
問題 求 Python程式碼 from numpy import exp def f(x): """被積函式e^(x^2)""" return exp(pow(x,2)) def simpson(a,b): """辛普森公式""" return (b-a)*(f(a)+