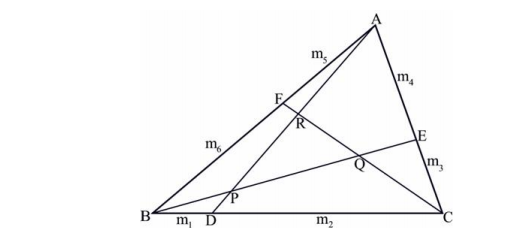
題意：如圖所示，給出P、Q、R三點的座標，AB、BC、AC被點F、D、E劃分成m1:m2、m3:m4、m5:m6，給出m1~m6的數值，求△ABC的三個頂點A、B、C的座標。

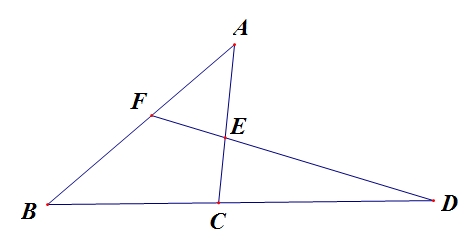
題解：根據梅涅勞斯定理，如果有兩個三角形是這樣組成的：

結論：(BD/DC)×(CE/EA)×(AF/FB)=1
證明省略，直接運用結論，在題中所給的三角形中有6組這樣的三角形，分別可以推出後面兩個邊的比值：
△CBQ 和 △CDR —-> DP / CQ
△BAP 和 △BFQ —-> FR / BP
△ACR 和 △APE —-> QE / AR
△CBE 和 △CDA —-> DP / PA
△BAD 和 △BFC —-> FR / CR
△ACF 和 △AEB —-> EQ / BQ
設DP為x，就能把全部邊都表示成關於x的式子，最後推回DP，就是一個關於x的一元一次方程，直接解方程就得到的DP的長度，進而所有邊的長度都可以求得，為了得到A、B、C的座標，讓點R在向量PR的方向上移動AR的距離就得到了A，其餘兩點類似得出。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const double PI = acos(-1);
const double eps = 1e-9;
struct Point {
    double x, y;
    Point(double a = 0, double b = 0): x(a), y(b) {}
};
typedef Point Vector;
double dcmp(double
 
 x) {
    if (fabs(x) < eps)
        return 0;
    return x < 0 ? -1 : 1;
}
Vector operator + (const Point& A, const Point& B) {
    return Vector(A.x + B.x, A.y + B.y);
}
Vector operator - (const Point& A, const Point& B) {
    return Vector(A.x - B.x, A.y - B.y);
}
Vector operator
 
 * (const Point& A, double a) {
    return Vector(A.x * a, A.y * a);
}
Vector operator / (const Point& A, double a) {
    return Vector(A.x / a, A.y / a);
}
double Cross(const Vector& A, const Vector& B) {
    return A.x * B.y - A.y * B.x;
}
double Dot(const Vector& A, const Vector& B) {
    return A.x * B.x + A.y * B.y;
}
double Length(const Vector& A) {
    return sqrt(Dot(A, A));
}
bool operator < (const Point& A, const Point& B) {
    return A.x < B.x || (A.x == B.x && A.y < B.y);
}
bool operator == (const Point& A, const Point& B) {
    return A.x == B.x && A.y == B.y;
}

Point P, Q, R;
double m1, m2, m3, m4, m5, m6; 

int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        scanf("%lf%lf%lf%lf%lf%lf", &P.x, &P.y, &Q.x, &Q.y, &R.x, &R.y);
        scanf("%lf%lf%lf%lf%lf%lf", &m1, &m2, &m3, &m4, &m5, &m6);
        double RP = Length(P - R);
        double RQ = Length(R - Q);
        double PQ = Length(P - Q);
        double t1 = m1 * RP / (m1 + m2) / RQ; // DP / CQ
        double t2 = m5 * RQ / (m5 + m6) / PQ; // FR / BP
        double t3 = m3 * PQ / (m3 + m4) / RP; // QE / AR
        double t4 = m1 * m3 / (m1 + m2) / m4; // DP / PA
        double t5 = m1 * m5 / (m5 + m6) / m2; // FR / CR
        double t6 = m3 * m5 / (m3 + m4) / m6; // EQ / BQ
        double DP = (t4 * RP + t6 * t4 * PQ / t3 + t6 * t5 * t4 * RQ / t3 / t2) / (1 - t6 * t5 * t4 / t3 / t2 / t1);
        double AR = DP / t4 - RP;
        Point A = R + (R - P) * (AR / RP);
        double BP = t5 / t2 * (DP / t1 + RQ);   
        Point B = P + (P - Q) * (BP / PQ);
        double CQ = DP / t1;
        Point C = Q + (Q - R) * (CQ / RQ);
        printf("%.8lf %.8lf %.8lf %.8lf %.8lf %.8lf\n", A.x, A.y, B.x, B.y, C.x, C.y);
    }
    return 0;
}