都說萬事開頭難，可一旦開頭，就是全新的狀態，就有可能收穫自己未曾預料到的成果。記錄是為了更好的監督、理解和推進，學習過程中用到的資料集和程式碼都將上傳到github

　　迴歸是對一個或多個自變數和因變數之間的關係進行建模，求解的一種統計方法，之前的部落格中總結了線上性迴歸中使用最小二乘法推導最優引數的過程和logistic迴歸，接下來將對最小二乘法、區域性加權迴歸、嶺迴歸和前向逐步迴歸演算法進行依次說明和總結

1. 用線性迴歸找到最佳擬合曲線

（1）迴歸的一般方法

　　收集資料：採用任意方法收集資料

　　準備資料：迴歸需要數值型資料，標稱型資料將被轉成數值型資料

　　分析資料：繪出資料的視覺化二維圖將有助於對資料做出理解和分析，在採用縮減法求得新迴歸係數之後，可以將新擬合線繪在圖上作為對比

　　訓練演算法：找到迴歸係數

　　測試演算法：使用R²或者預測值和資料的擬合度，來分析模型的效果

　　使用演算法：使用迴歸，可以在給定輸入的時候預測出一個數值，這是對分類方法的提升，因為這樣可以預測連續性資料而不僅僅是離散的類別標籤

（2）需求

　　對dataset/ex0.txt檔案中的資料集採用線性迴歸找到最擬合直線，資料集：https://github.com/lizoo6zhi/MachineLearn.samples/tree/master/dataset

（3）繪製資料的視覺化二維圖

（4）通過最小二乘法得到最優引數

　　前面我們已經推導過使用最小二乘法求最優引數：

　　程式碼實現：

def stand_regres(dataset,label):
    """
    標準線性迴歸函式
    dataset:list
    label:list
    """
    X = np.mat(dataset)
    Y = np.mat(label).T

    temp = X.T * X
    if np.linalg.det(temp) == 0.0:  #計算行式的值
        print("X.T*X沒有逆矩陣")
        return 
    else:
        temp = temp.I * X.T * Y
    
 
return temp

　　注意上面程式碼中紅色標記處，通過計算行列式的值判斷X.T*X是否有逆矩陣

（5）通過計算出的最優引數對樣本進行迴歸測試，並繪製擬合曲線

def plot_stand_regress(dataset,label,ws,ax):
    """
    繪製資料集和擬合曲線
    """
    dataset_matrix = np.mat(dataset)
    x = dataset_matrix[:,1]
    y = label
    cal_y = dataset * ws
    ax.scatter(x.T.getA(),y,s=10,c='red')
    ax.plot(x,cal_y)

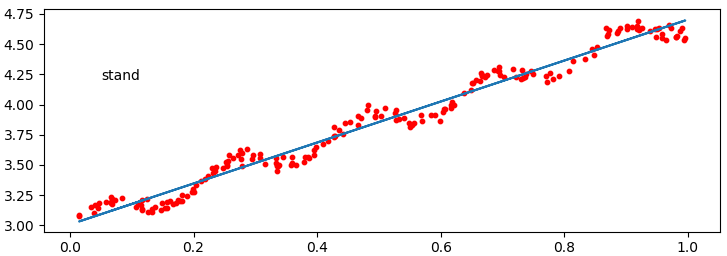
（6）在python中，NumPy庫提供了相關係數的計算方法，可以通過corrcoef(yEstimate,yActual)來計算預測值與真實值的相關性

print(np.corrcoef(cal_y.T,np.mat(y)))

　　從上圖可以看出，預測值與真實值之間的相關係數為0.98647356

　　最佳擬合直線方法將資料視為直線進行建模，具有十分不錯的效果，但若是資料的離散程度很大呢，那該怎麼辦？

2. 區域性加權線性迴歸

　　我們現實生活中的很多資料不一定都能用線性模型描述。比如房價問題，很明顯直線非但不能很好的擬合所有資料點，而且誤差非常大，但是一條類似二次函式的曲線卻能擬合地很好。為了解決非線性模型建立線性模型的問題，我們預測一個點的值時，對這個點附近的點設定權值。基於這個思想，便產生了區域性加權線性迴歸演算法。在這個演算法中，其他離一個點越近，權重越大，對迴歸係數的貢獻就越多。損失函式如下：
　　
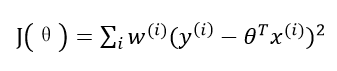
　　其中w(i)是權重，它根據要預測的點與資料集中的點的距離來為資料集中的點賦權值，當某點離要預測的點越遠，其權重越小，否則越大。一個比較好的權重函式如下：

　　
 
　　該函式稱為指數衰減函式，其中k為波長引數，它控制了權值隨距離下降的速率，該函式形式上類似高斯分佈(正態分佈)，但並沒有任何高斯分佈的意義。該演算法解出迴歸係數如下：

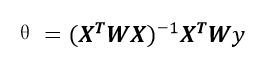
（1）需求

　　使用區域性加權線性迴歸對dataset/ex0.txt檔案中的資料集進行曲線擬合

（2）實現

def lwrw(test_point, xarray, yarray, k = 1.0):
    """
    區域性加權迴歸函式(locally weighted linear regression)
    dataset:list
    label:list
    """
    mat_x = np.mat(xarray)
    mat_y = np.mat(yarray).T
    row,col = np.shape(mat_x)    
    weights = np.mat(np.eye(row))
    for i in range(row):
        diffmat = test_point - mat_x[i,:]
        weights[i,i] = np.exp((diffmat*diffmat.T)/(-2.0*k*k))
    temp = mat_x.T * weights * mat_x
    if np.linalg.det(temp) == 0.0:
        print("mat_x.T * weights * X沒有逆矩陣")
        return 
    else:
        temp = temp.I * mat_x.T * weights * mat_y
    return test_point*temp

（3）測試

　　分別設定k為0.01和0.003，當k=1時擬合效果和最小二乘法擬合效果一樣

def plot_lwrw_regress(dataset,label,cal_y_list,ax):
    """
    繪製資料集和擬合曲線
    """
    dataset_matrix = np.mat(dataset)
    x = dataset_matrix[:,1]
    y = label
    ax.scatter(x.T.getA(),y,s=10,c='red')
    #對dataset進行排序
    sorted_index = x.argsort(0)
    sorted_x = dataset_matrix[sorted_index][:,0,:] #關鍵
    ax.plot(sorted_x[:,1],cal_y_list[sorted_index])

if __name__ == "__main__":
    dataset,label = load_dataset('dataset/ex0.txt')
    fig = plt.figure()
    
    #當k為0.01時
    for row in range(rows):
        cal_y = lwrw(dataset[row],dataset,label,0.01)
        x_y_map[row] = cal_y
    ax = fig.add_subplot(323)
    ax.text(0.05,4.2,'k=0.01')
    plot_lwrw_regress(dataset,label,x_y_map,ax)
    
    #當k為0.003
    for row in range(rows):
        cal_y = lwrw(dataset[row],dataset,label,0.003)
        x_y_map[row] = cal_y
    ax = fig.add_subplot(325)
    ax.text(0.05,4.2,'k=0.003')
    plot_lwrw_regress(dataset,label,x_y_map,ax)
    
    plt.show()

　　效果：

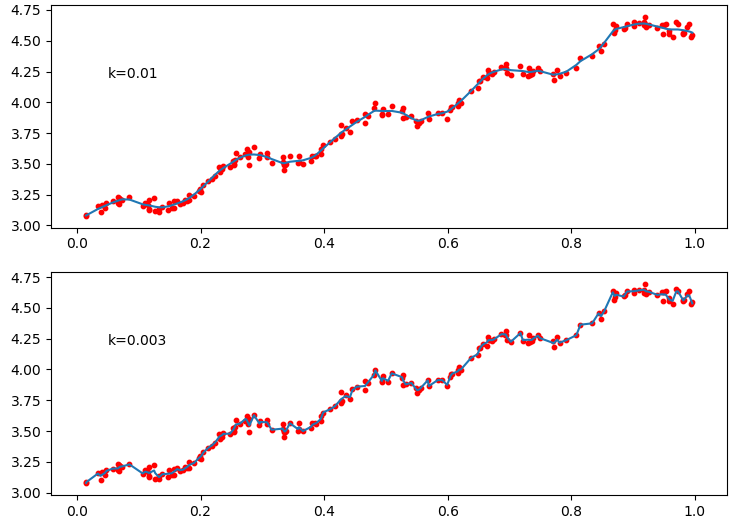
　　大家可以通過不同的k係數測試效果，區域性加權線性迴歸存在一個問題就是增加了計算量，因為它對每個點做預測時都必須使用整個資料集

3. 嶺迴歸

　　思考下，如果資料的特徵比樣本還多應該怎麼辦？是否還可以使用線性迴歸和之前的方法來做預測？

　　答案是否定的，即不能再使用前面介紹的方法，這是因為在計算（X.T*X)的逆矩陣的時候會出錯

　　有逆矩陣的矩陣一定是方正，但方正不一定有逆矩陣，只有方正的行列式不為0時才有逆矩陣

　　為了解決整個問題，統計學家引入了嶺迴歸（ridge regression）的概念，簡單的說，嶺迴歸就是在X.T * X上加一個λI使得矩陣非奇異，進而確保（X.T * X + λI）一定可逆，其中I為m*m的單位矩陣，λ是使用者定義的一個數值，我們可以通過測試使用不同的λ引數來確定最優λ

　　嶺迴歸與多項式迴歸唯一的不同在於代價函式上的差別。嶺迴歸的代價函式如下：

　　為了方便計算導數，通常也寫成下面的形式：

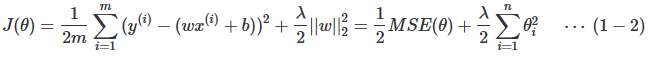
　　上式中的w是長度為n的向量，不包括截距項的係數θ0；θθ是長度為n+1的向量，包括截距項的係數θ0；m為樣本數；n為特徵數

　　嶺迴歸的代價函式仍然是一個凸函式，因此可以利用梯度等於0的方式求得全域性最優解（正規方程）：

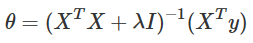
（1）需求

　　通過視覺化圖形描述λ與迴歸係數之間的關係

（2）實現

　　通過以e為底的指數函式設定λ的值，如：exp(i-10)，i為[0,30]，同公式計算不同λ下回歸係數的變化

（3）程式碼

def ridge_regres(xarray,yarray,lam=0.2):
    """
    嶺迴歸
    處理當特徵比樣本點還多，也酒水說輸入資料的矩陣X不是滿秩矩陣，非滿秩矩陣在求逆時會出現問題
    w = (X.T*X + rI).I * X.T * Y
    """
    xmat = np.mat(xarray)
    ymat = np.mat(yarray).T
    xtx = xmat.T * xmat
    denom = xtx + np.eye(np.shape(xmat)[1])*lam
    if np.linalg.det(denom) == 0.0:
        print('denom 沒有逆矩陣')
    ws = denom.I * xmat.T * ymat
    return ws
    
def ridge_test(xarray,yarray,ax):
    xmat = np.mat(xarray)
    row,col = np.shape(xmat)
    ymat = np.mat(yarray)
    xmean,xvar = data_normalize(xarray) #對資料進行標準化處理
    np.seterr(divide='ignore',invalid='ignore')
    xmat = (xmat - xmean) / xvar
    num_test_pts = 30
    wmat = np.ones((num_test_pts,col))
    
    lam_list = []
    for i in range(num_test_pts):
        lam = np.exp(i-10)
        lam_list.append(i-10)
        ws = ridge_regres(xarray,yarray,lam)
        wmat[i,:] = ws.T
    
    #繪製不同lam情況下引數變化情況
    for j in range(np.shape(wmat)[1]):
        ax.plot(lam_list,wmat[:,j])

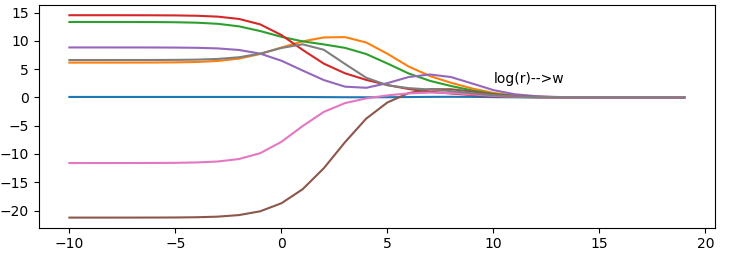
　　效果：

　　x軸為i的取值，y軸為迴歸係數值，從圖可以看出當λ非常小時，係數和普通迴歸一樣，當λ非常大時，所有迴歸係數都縮減為0，因此，我們可以在中間某處找到是的預測的結果最好的λ值

　　以下為λ=0.02的效果圖

　　這樣我們可以結合區域性加權和嶺迴歸計算最優迴歸係數，還有其他一些縮減方法，如lasso、LAR、PCA迴歸以及子集選擇等，這些方法不僅可以提高預測精確率，而且還可以解釋迴歸係數，將後續進行總結

　　再使用嶺迴歸對資料集dataset/abalone.txt測試，看看回歸係數變化

4. 前向逐步迴歸

　　前向逐步迴歸演算法可以得到與lasso差不多的效果，但更加簡單。前向迴歸演算法屬於一種貪心演算法，即每一步都儘可能減少誤差，一開始，所有的權重都設為1，然後每一步所作的決策是對某個權重增加或減少一個很小的值

　　虛擬碼如下：　

資料標準化，使其分佈滿足0均值和單位方差
在每輪迭代過程中：
    設定當前最小誤差lowestError為正無窮
    對每個特徵：
        增大或減少：
            改變一個係數得到一個新的w
            計算新w下的誤差
            如果誤差error小於當前最小誤差：設定wbest等於當前的w
        將當前w設定為新的wbest

（1）需求

　　使用前向逐步迴歸演算法，算出最優迴歸引數，並可視化顯示迴歸引數隨迭代次數的變化情況，最後標準迴歸演算法進行比較

（2）程式碼實現

def stage_wise(dataset,label,step,numiter=100):
    """
    前向逐步迴歸
    """
    xmat = np.mat(dataset)
    xmean,xvar = data_normalize(dataset) #平均值和標準差
    ymat = np.mat(label).T
    ymat = ymat - np.mean(ymat,0)
    xmat = (xmat - xmean) / xvar
    m,n = np.shape(xmat)
    return_mat = np.zeros((numiter,n))
    ws = np.zeros((n,1))
    ws_test = ws.copy()
    ws_max = ws.copy()
    
    for iter in range(numiter):  #迭代次數
        lowest_error = np.inf
        for j in range(n):  #對每個特徵進行變數
            for sign in [-1,1]:
                ws_test = ws.copy()
                ws_test[j] += step*sign
                ytest = xmat * ws_test
                rssE = ((ymat.A-ytest.A)**2).sum()
                if rssE < lowest_error:
                    lowest_error = rssE
                    ws_max = ws_test
        ws = ws_max.copy()
        return_mat[iter,:] = ws.T
    return return_mat    

def stage_wise_test(ws_mat,iternum,ax):
    """
    前向逐步迴歸演算法中迴歸係數隨迭代次數的變化情況
    """    
    x = range(iternum)
    for i in range(np.shape(ws_mat)[1]):
        ax.plot(x,ws_mat[:,i])

（3）測試，輸出視覺化效果

#前向逐步迴歸
ax = fig.add_subplot(326)
ws = stage_wise(dataset,label,0.01,500)
print("前向逐步迴歸經過迭代後的最後迴歸係數：",ws[-1,:])
stage_wise_test(ws,500,ax)

　　效果：

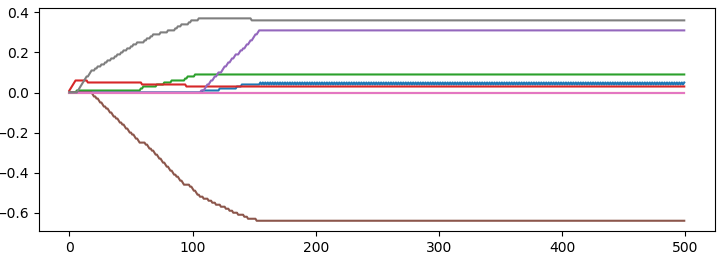
　　上圖表示了迴歸係數隨迭代次數的變化情況，當迭代150次時，迴歸係數穩定分別為：

（4）接下來使用標準迴歸演算法，也就是最小二乘法對dataset/abalone.txt資料集進行測試，計算迴歸係數

    #使用標準迴歸對"dataset/abalone.txt"資料集進行測試
    #對資料進行標準化處理
    xman,xvar = data_normalize(dataset)
    xmat = np.mat(dataset)
    xmat = (xmat - xman) / xvar
    ymat = np.mat(label)
    ax = stand_regres(xmat,ymat)
    print("標準迴歸後得到的迴歸係數：",ws[-1,:])

　　最終輸出結果和前向逐步迴歸算出係數一樣：

5. 總結

　　與分類一樣，迴歸也是預測目標值的過程，迴歸與分類的不同點在於，前者預測連續性變數，而後者預測離散型變數，迴歸是統計學中最有力的工具之一，在迴歸方程裡，求得特徵對應的最佳迴歸係數的方法是最小 化誤差的平方和，給定輸入的矩陣X，如果X.T * X的逆存在並可以求得的化，迴歸法可以直接使用，資料集上計算出的迴歸方程並不一定意味著它是最佳的，可以使用預測值yHat和原始值y的相關性來度量回歸方程的好壞。　

　　當資料的樣本數比特徵數還少的時候，矩陣X.T * X的逆不能直接計算，即便當樣本數比特徵數多時，X.T * X的逆仍可能無法直接計算，這是因為特徵有可能高度相關，這時可以考慮使用嶺迴歸，因為當X.T * X的逆不能計算時，它仍保證能求得迴歸係數

　　嶺迴歸是縮減法的一種，相當於對迴歸係數的大小施加了限制，另一種很好的縮減法是lasso,lasso難以求解，但可以 使用計算簡便的逐步線性迴歸方法來求得近似解

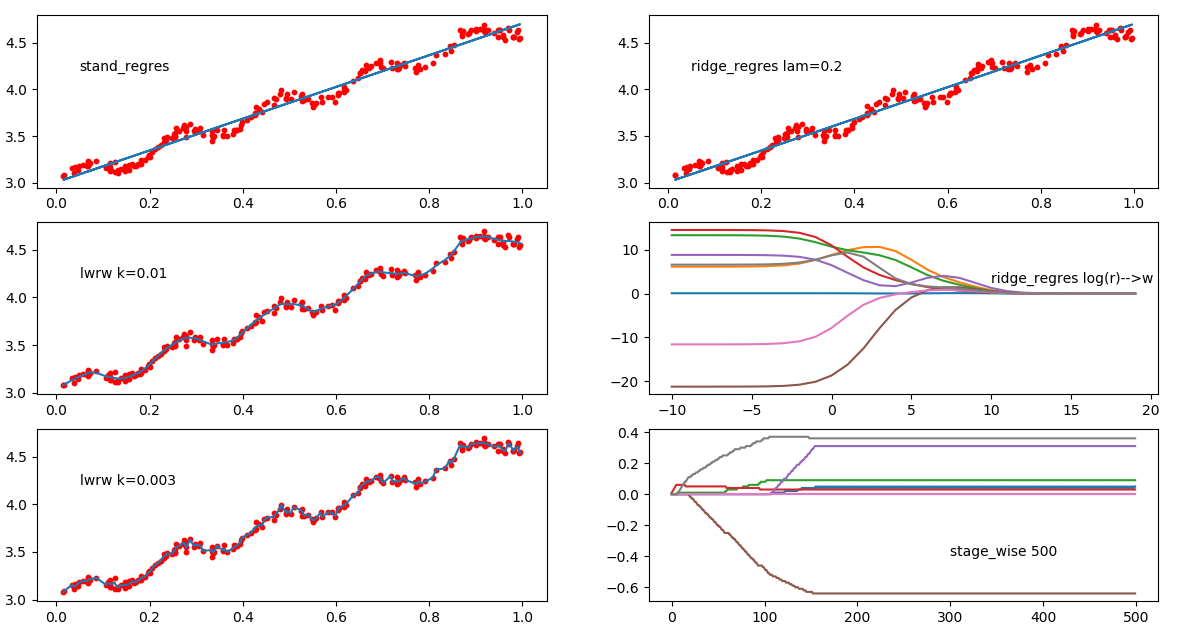
　　最後來張綜合圖：