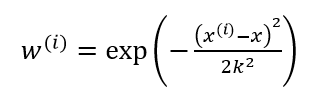【機器學習】區域性加權線性迴歸
一、問題引入
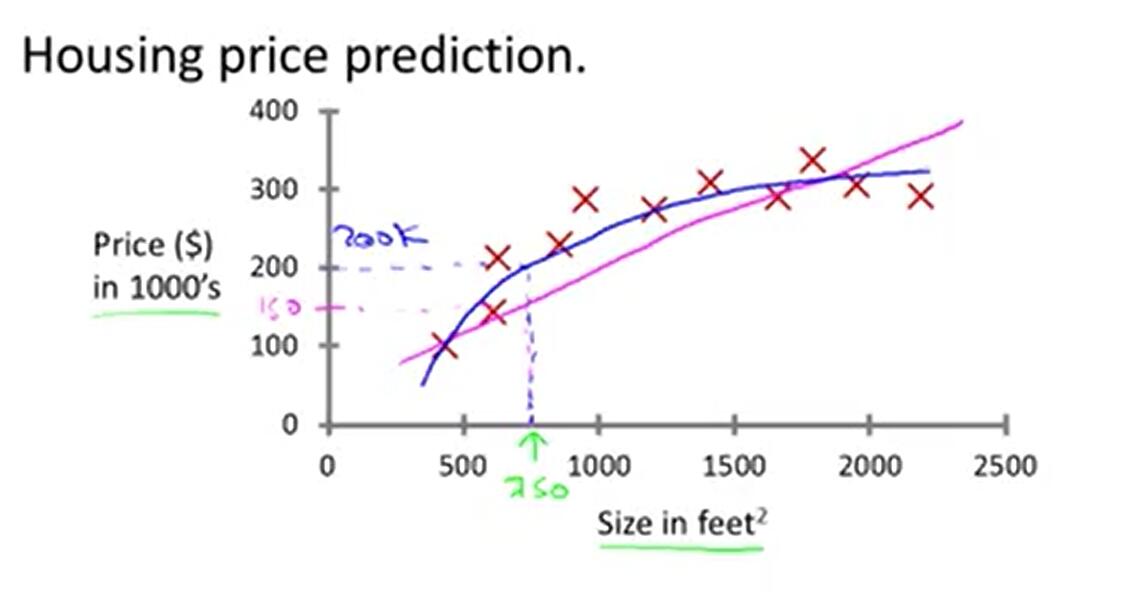
我們現實生活中的很多資料不一定都能用線性模型描述。依然是房價問題,很明顯直線非但不能很好的擬合所有資料點,而且誤差非常大,但是一條類似二次函式的曲線卻能擬合地很好。為了解決非線性模型建立線性模型的問題,我們預測一個點的值時,選擇與這個點相近的點而不是所有的點做線性迴歸。基於這個思想,便產生了區域性加權線性迴歸演算法。在這個演算法中,其他離一個點越近,權重越大,對迴歸係數的貢獻就越多。
二、問題分析
本演算法依然使用損失函式J,只不過是加權的J函式:
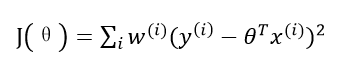
其中w(i)是權重,它根據要預測的點與資料集中的點的距離來為資料集中的點賦權值。當某點離要預測的點越遠,其權重越小,否則越大。一個比較好的權重函式如下:
該函式稱為指數衰減函式,其中k為波長引數,它控制了權值隨距離下降的速率,該函式形式上類似高斯分佈(正態分佈),但並沒有任何高斯分佈的意義。該演算法解出迴歸係數如下:
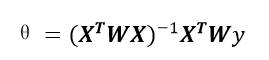
在使用這個演算法訓練資料的時候,不僅需要學習線性迴歸的引數,還需要學習波長引數。這個演算法的問題在於,對於每一個要預測的點,都要重新依據整個資料集計算一個線性迴歸模型出來,使得演算法代價極高。
三、程式碼實現
1.Matlab版
(1) 區域性加權線性迴歸函式
% 對所有點計算估計值
function yHat = lwlr(testMat, xMat, yMat, k)
[row, ~] = size(testMat);
yHat = zeros (2) 匯入資料並繪圖
clc;
clear all;
data = load('D:\\ex0.txt');
x = data(:,1:2);
y = data(:,3);
y_hat = lwlr(x, x, y, 0.01); % 呼叫區域性加權線性迴歸函式計算估計值
x_axis = (x(:, 2))'; % x座標軸為x矩陣的第二列資料
y_axis = y';
sort(x_axis); % 對x向量升序排列
plot(x_axis, y, 'r.'); % 散點圖
hold on
plot(x_axis, y_hat, 'b.'); %迴歸曲線圖
(3) 分別選取k=1.0,0.01,0.003繪圖如下:
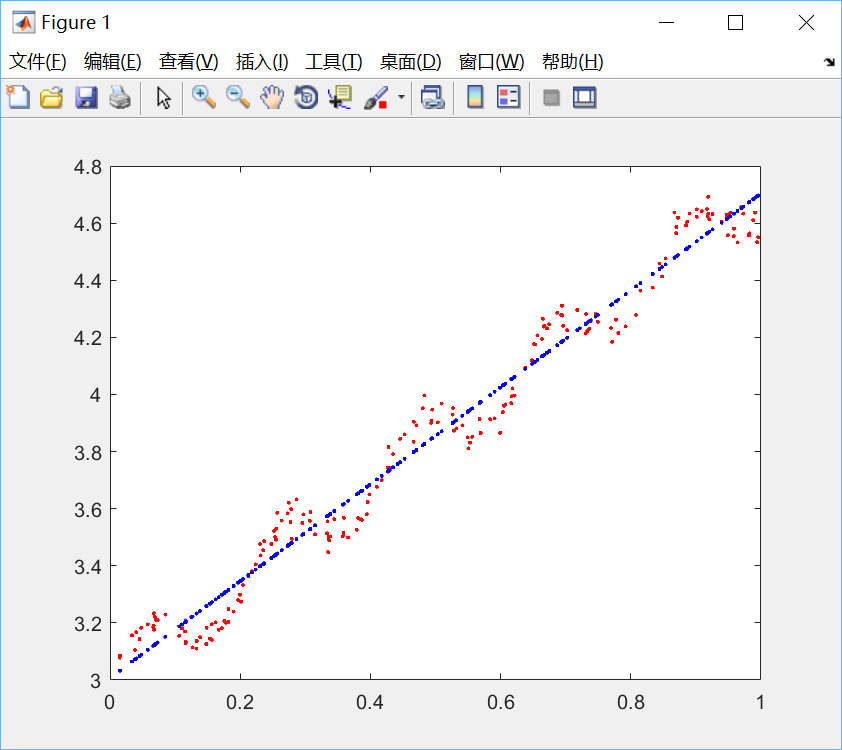
圖1 k=1.0 欠擬合
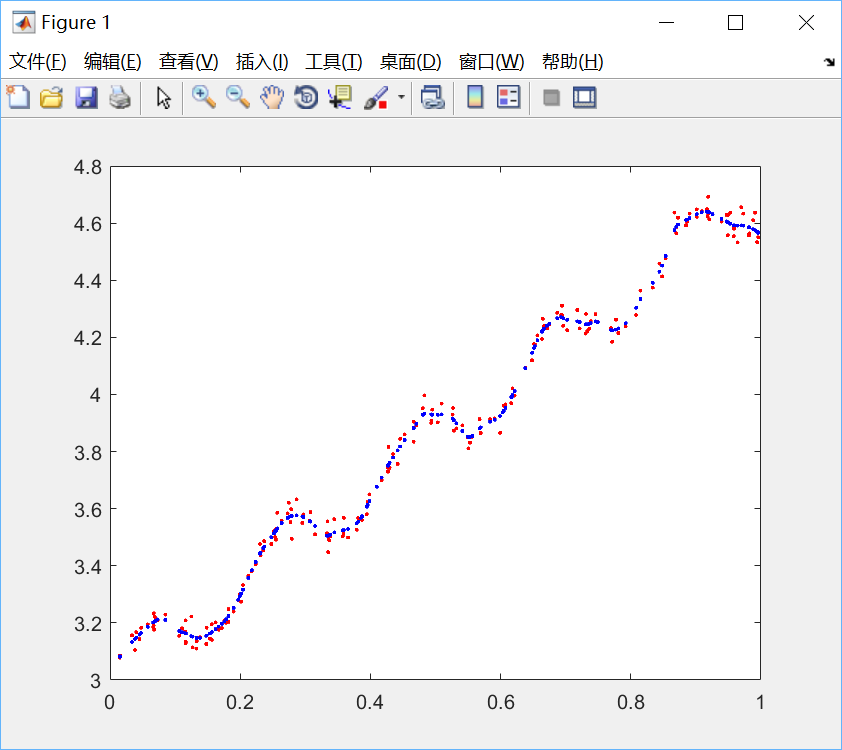
圖2 k=0.01 最佳擬合
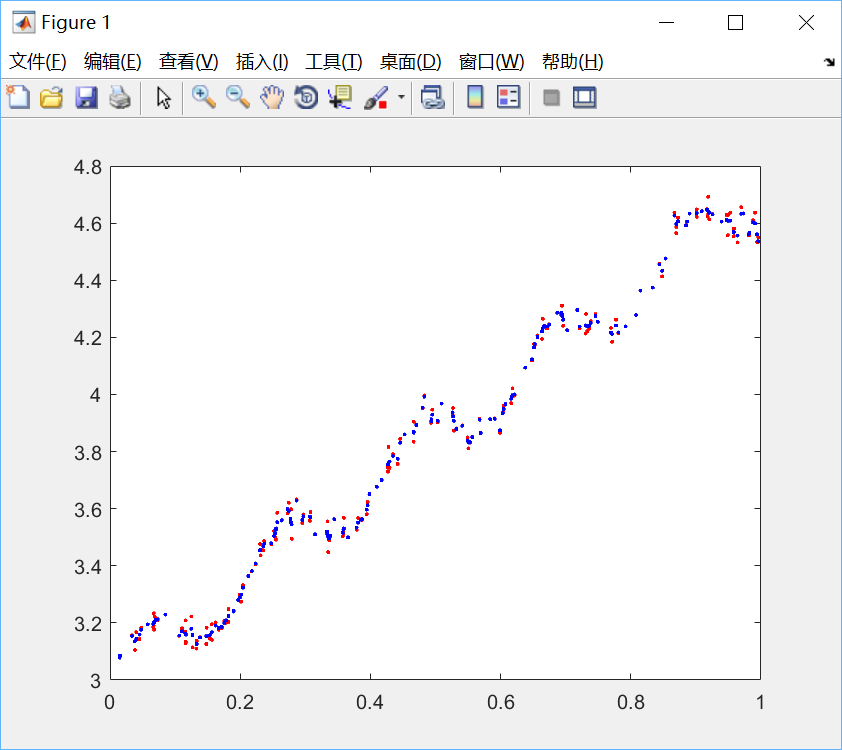
圖3 k=0.003 過擬合
2.Python版
(1)區域性加權線性迴歸函式
from numpy import *
# 對某一點計算估計值
def lwlr(testPoint, xArr, yArr, k = 1.0):
xMat = mat(xArr); yMat = mat(yArr).T
m = shape(xMat)[0]
weights = mat(eye((m)))
for i in range(m):
diffMat = testPoint - xMat[i, :]
weights[i, i] = exp(diffMat * diffMat.T/(-2.0 * k**2)) # 計算權重對角矩陣
xTx = xMat.T * (weights * xMat) # 奇異矩陣不能計算
if linalg.det(xTx) == 0.0:
print('This Matrix is singular, cannot do inverse')
return
theta = xTx.I * (xMat.T * (weights * yMat)) # 計算迴歸係數
return testPoint * theta
# 對所有點計算估計值
def lwlrTest(testArr, xArr, yArr, k = 1.0):
m = shape(testArr)[0]
yHat = zeros(m)
for i in range(m):
yHat[i] = lwlr(testArr[i], xArr, yArr, k)
return yHat(2)匯入資料並繪圖
import matplotlib.pyplot as plt
from locally_weighted_linear_regression import LocallyWeightedLinearRegression as lwlr
from numpy import *
xArr, yArr = lwlr.loadDataSet('ex0.txt')
yHat = lwlr.lwlrTest(xArr, xArr, yArr, 0.01)
xMat = mat(xArr)
strInd = xMat[:, 1].argsort(0)
xSort = xMat[strInd][:, 0, :]
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(xSort[:, 1], yHat[strInd])
ax.scatter(xMat[:, 1].flatten().A[0], mat(yArr).T.flatten().A[0], s = 2, c = 'red')
plt.show()(3)分別選取k=1.0,0.01,0.003繪圖如下:
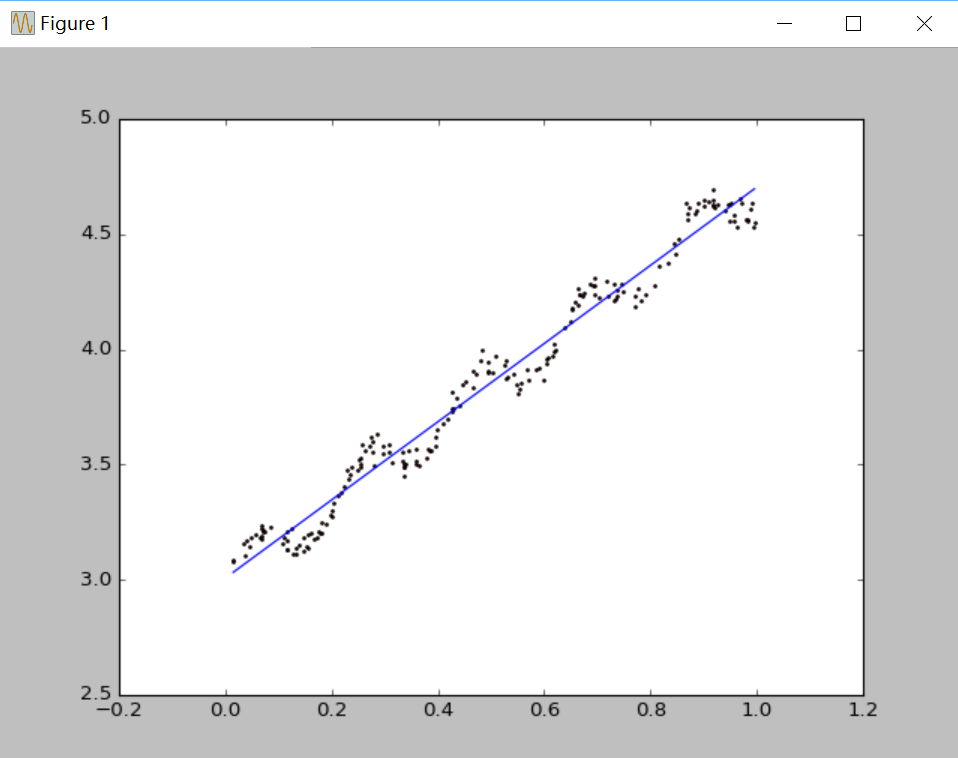
圖1 k=1.0 欠擬合
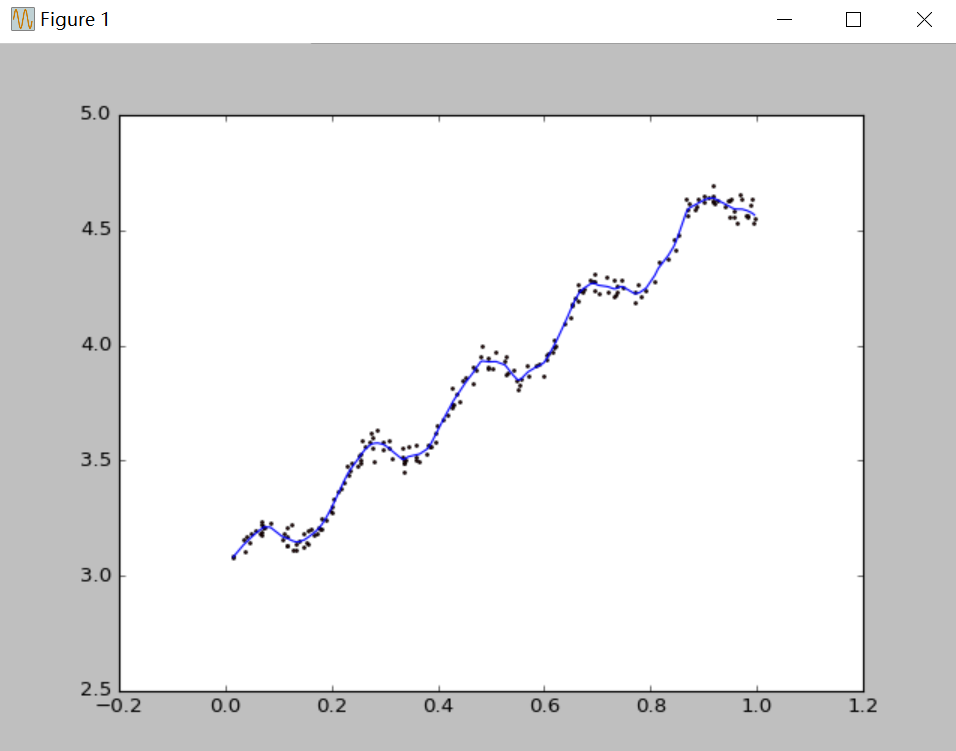
圖2 k=0.01 最佳擬合
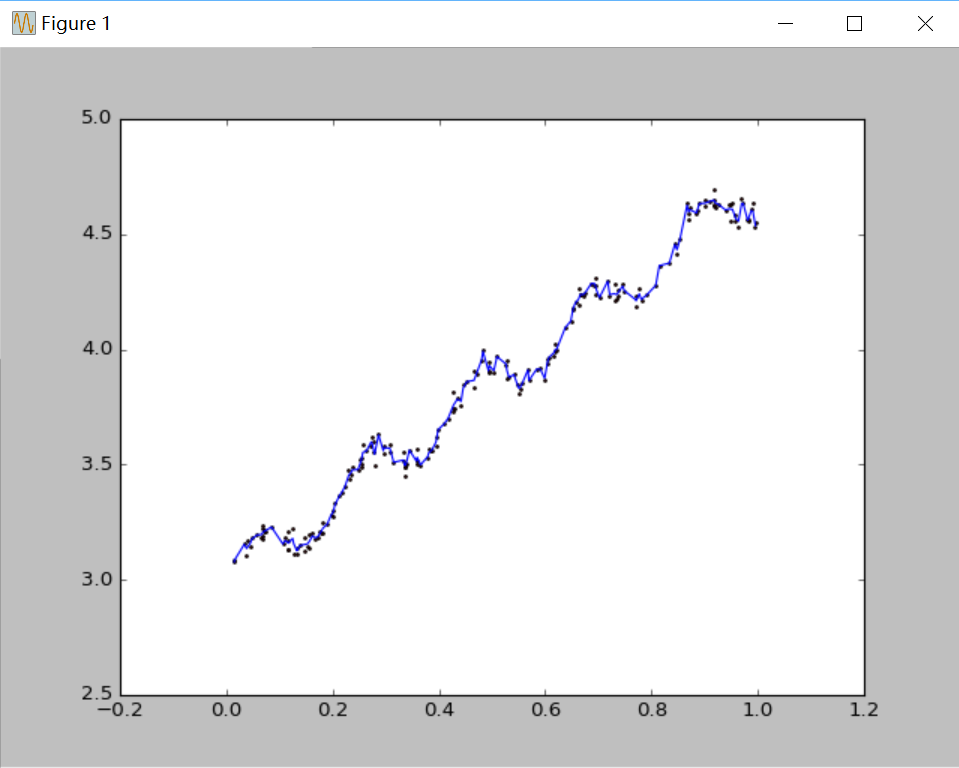
圖3 k=0.003 過擬合
四、結果分析:很明顯,當k=1.0時,迴歸曲線與散點圖欠擬合(underfitting),此時權重很大,如同將所有資料視為等權重,相當於普通線性迴歸模型;當k=0.01時得到了很好的效果;當k=0.003時,迴歸曲線與散點圖過擬合(overfitting),由於納入了太多的噪聲點,擬合的直線與資料點過於貼近,此時也不屬於理想的模型。