大自然有種神奇的力量，它能夠將優良的基因保留下來，從而進化出更加強大、更加適合生存的基因。遺傳演算法便基於達爾文的進化論，模擬了自然選擇，物競天擇、適者生存，通過N代的遺傳、變異、交叉、複製，進化出問題的最優解。遺傳演算法看似神奇，但實現思路卻較為簡單。本文先跟大家介紹遺傳演算法的基本思想，然後用遺傳演算法來解決一個實際問題，最後給出遺傳演算法的程式碼實現和解析。廢話不多說，現在就開始吧～

遺傳演算法

在開始之前，我們先來了解下遺傳演算法中的幾個概念。

概念1：基因和染色體

在遺傳演算法中，我們首先需要將要解決的問題對映成一個數學問題，也就是所謂的“數學建模”，那麼這個問題的一個可行解即被稱為一條“染色體”。一個可行解一般由多個元素構成，那麼這每一個元素就被稱為染色體上的一個“基因”。

比如說，對於如下函式而言，[1,2,3]、[1,3,2]、[3,2,1]均是這個函式的可行解（代進去成立即為可行解），那麼這些可行解在遺傳演算法中均被稱為染色體。

3x+4y+5z<100

這些可行解一共有三個元素構成，那麼在遺傳演算法中，每個元素就被稱為組成染色體的一個基因。

概念2：適應度函式

在自然界中，似乎存在著一個上帝，它能夠選擇出每一代中比較優良的個體，而淘汰一些環境適應度較差的個人。那麼在遺傳演算法中，如何衡量染色體的優劣呢？這就是由適應度函式完成的。適應度函式在遺傳演算法中扮演者這個“上帝”的角色。

遺傳演算法在執行的過程中會進行N次迭代，每次迭代都會生成若干條染色體。適應度函式會給本次迭代中生成的所有染色體打個分，來評判這些染色體的適應度，然後將適應度較低的染色體淘汰掉，只保留適應度較高的染色體，從而經過若干次迭代後染色體的質量將越來越優良。

概念3：交叉

遺傳演算法每一次迭代都會生成N條染色體，在遺傳演算法中，這每一次迭代就被稱為一次“進化”。那麼，每次進化新生成的染色體是如何而來的呢？——答案就是“交叉”，你可以把它理解為交配。

交叉的過程需要從上一代的染色體中尋找兩條染色體，一條是爸爸，一條是媽媽。然後將這兩條染色體的某一個位置切斷，並拼接在一起，從而生成一條新的染色體。這條新染色體上即包含了一定數量的爸爸的基因，也包含了一定數量的媽媽的基因。

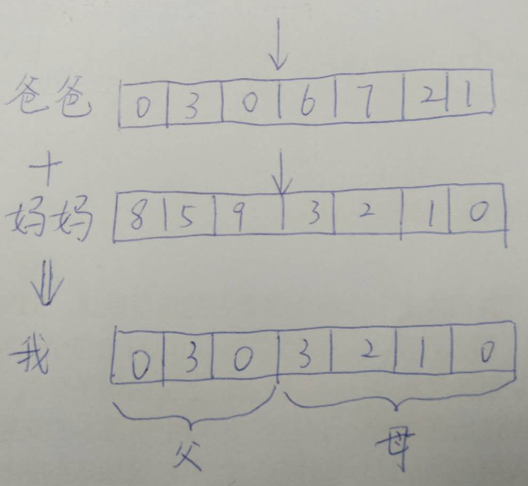
那麼，如何從上一代染色體中選出爸爸和媽媽的基因呢？這不是隨機選擇的，一般是通過輪盤賭演算法完成。

在每完成一次進化後，都要計算每一條染色體的適應度，然後採用如下公式計算每一條染色體的適應度概率。那麼在進行交叉過程時，就需要根據這個概率來選擇父母染色體。適應度比較大的染色體被選中的概率就越高。這也就是為什麼遺傳演算法能保留優良基因的原因。

染色體i被選擇的概率 = 染色體i的適應度 / 所有染色體的適應度之和

概念4：變異

交叉能保證每次進化留下優良的基因，但它僅僅是對原有的結果集進行選擇，基因還是那麼幾個，只不過交換了他們的組合順序。這隻能保證經過N次進化後，計算結果更接近於區域性最優解，而永遠沒辦法達到全域性最優解，為了解決這一個問題，我們需要引入變異。

變異很好理解。當我們通過交叉生成了一條新的染色體後，需要在新染色體上隨機選擇若干個基因，然後隨機修改基因的值，從而給現有的染色體引入了新的基因，突破了當前搜尋的限制，更有利於演算法尋找到全域性最優解。

概念5：複製

每次進化中，為了保留上一代優良的染色體，需要將上一代中適應度最高的幾條染色體直接原封不動地複製給下一代。

假設每次進化都需生成N條染色體，那麼每次進化中，通過交叉方式需要生成N-M條染色體，剩餘的M條染色體通過複製上一代適應度最高的M條染色體而來。

遺傳演算法的流程

通過上述概念，相信遺傳演算法的大致原理你已經瞭解，下面我們將這些概念串聯起來，介紹遺傳演算法的執行流程。

• 在演算法初始階段，它會隨機生成一組可行解，也就是第一代染色體。

• 然後採用適應度函式分別計算每一條染色體的適應程度，並根據適應程度計算每一條染色體在下一次進化中被選中的概率(這個上面已經介紹，這裡不再贅述)。

上面都是準備過程，下面正式進入“進化”過程。

• 通過“交叉”，生成N-M條染色體；

• 再對交叉後生成的N-M條染色體進行“變異”操作；

• 然後使用“複製”的方式生成M條染色體；

到此為止，N條染色體生成完畢！緊接著分別計算N條染色體的適應度和下次被選中的概率。

這就是一次進化的過程，緊接著進行新一輪的進化。

究竟需要進化多少次？

每一次進化都會更優，因此理論上進化的次數越多越好，但在實際應用中往往會在結果精確度和執行效率之間尋找一個平衡點，一般有兩種方式。

1. 限定進化次數

在一些實際應用中，可以事先統計出進化的次數。比如，你通過大量實驗發現：不管輸入的資料如何變化，演算法在進化N次之後就能夠得到最優解，那麼你就可以將進化的次數設成N。

然而，實際情況往往沒有那麼理想，往往不同的輸入會導致得到最優解時的迭代次數相差甚遠，這是你可以考慮採用第二種方式。

2. 限定允許範圍

如果演算法要達到全域性最優解可能要進過很多很多很多次的進化，這極大影響系統的效能。那麼我們就可以在演算法的精確度和系統效率之間尋找一個平衡點。我們可以事先設定一個可以接收的結果範圍，當演算法進行X次進化後，一旦發現了當前的結果已經在誤差範圍之內了，那麼就終止演算法。

但這種方式也有個缺點，有些情況下可能稍微進化幾次就進入了誤差允許範圍，但有些情況下需要進化很多很多很多很多次才能進入誤差允許範圍。這種不確定性導致演算法的執行效率不可控。

所以，究竟選擇何種方式來控制演算法的迭代次數，這需要你根據具體的業務場景合理地選擇。這裡無法給出普世的方式，需要你自己在真實的實踐中找到答案。

採用遺傳演算法解決負載均衡排程問題

演算法都是用來解決實際問題的，到此為止，我想你對遺傳是演算法已經有了個全面的認識，下面我們就用遺傳演算法來解決一個實際問題——負載均衡排程問題。

假設有N個任務，需要負載均衡器分配給M個伺服器節點去處理。每個任務的任務長度、每臺伺服器節點(下面簡稱“節點”)的處理速度已知，請給出一種任務分配方式，使得所有任務的總處理時間最短。

數學建模

拿到這個問題後，我們首先需要將這個實際問題對映成遺傳演算法的數學模型。

任務長度矩陣（簡稱：任務矩陣）

我們將所有任務的任務長度用矩陣tasks表示，如：

Tasks={2,4,6,8}

那麼，tasks[i]中的i表示任務的編號，而tasks[i]表示任務i的任務長度。

節點處理速度矩陣（簡稱：節點矩陣）

我們將所有伺服器節點的處理速度用矩陣nodes表示，如：

Nodes={2,1}

那麼，nodes[j]中的j表示節點的編號，而nodes[j]表示節點j的處理速度。

任務處理時間矩陣

當 任務矩陣Tasks和節點矩陣Nodes確定下來之後，那麼所有任務分配給所有節點的任務處理時間都可以確定了，我們用矩陣timeMatrix表示，它是一個二維陣列：

1 2
2 4
3 6
4 8

timeMatrix[i][j]表示將任務i分配給節點j處理所需的時間，它通過如下公式計算：

timeMatrix[i][j] = tasks[i]/nodes[j]

染色體

通過上文我們知道，每次進化都會產生N條染色體，每一條染色體都是當前問題的一個可行解，可行解由多個元素構成，每個元素稱為染色體的一個基因。下面我們就用一個染色體矩陣來記錄演算法每次進化過程中的可行解。

一條染色體的構成如下：

chromosome={1,2,3,4}

一條染色體就是一個一位陣列，一位陣列的下標表示任務的編號，陣列的值表示節點的編號。那麼chromosome[i]=j的含義就是：將任務i分配給了節點j。

上面的例子中，任務集合為Tasks={2,4,6,8}，節點集合為Nodes={2,1}，那麼染色體chromosome={3,2,1,0}的含義是：

• 將任務0分配給3號節點
• 將任務1分配給2號節點
• 將任務2分配給1號節點
• 將任務3分配給0號節點

適應度矩陣

通過上文可知，在遺傳演算法中扮演者“上帝”角色的是適應度函式，它會評判每一條染色體的適應度，並保留適應度高的染色體、淘汰適應度差的染色體。那麼在演算法實現時，我們需要一個適應度矩陣，記錄當前N條染色體的適應度，如下所示：

adaptability={0.6, 2, 3.2, 1.8}

adaptability陣列的下標表示染色體的編號，而adaptability[i]則表示編號為i的染色體的適應度。

在負載均衡排程這個例項中，我們將N個任務執行總時長作為適應度評判的標準。當所有任務分配完後，如果總時長較長，那麼適應度就越差；而總時長越短，則適應度越高。

選擇概率矩陣

通過上文可知，每次進化過程中，都需要根據適應度矩陣計算每一條染色體在下一次進化中被選擇的概率，這個矩陣如下所示：

selectionProbability={0.1, 0.4, 0.2, 0.3}

矩陣的下標表示染色體的編號，而矩陣中的值表示該染色體對應的選擇概率。其計算公式如下：

selectionProbability[i] = adaptability[i] / 適應度之和

遺傳演算法的實現

上述一切知識點鋪墊完成之後，接下來我們就可以上程式碼了，相信Talk is cheap, show you the code!

/**
 * 遺傳演算法
 * @param iteratorNum 迭代次數
 * @param chromosomeNum 染色體數量
 */
function gaSearch(iteratorNum, chromosomeNum) {
    // 初始化第一代染色體
    var chromosomeMatrix = createGeneration();

    // 迭代繁衍
    for (var itIndex=1; itIndex<iteratorNum; itIndex++) {
        // 計算上一代各條染色體的適應度
        calAdaptability(chromosomeMatrix);

        // 計算自然選擇概率
        calSelectionProbability(adaptability);

        // 生成新一代染色體
        chromosomeMatrix = createGeneration(chromosomeMatrix);

    }
}

程式碼一來，一切都清晰了，似乎不需要過多的解釋了。
上面是遺傳演算法最主要的框架，其中的一些細節封裝在了一個個子函式中。在理解了遺傳演算法的原理後，我想程式碼不需要我作過多的解釋了吧～完整的程式碼在我的Github上，歡迎Star。

結果展示

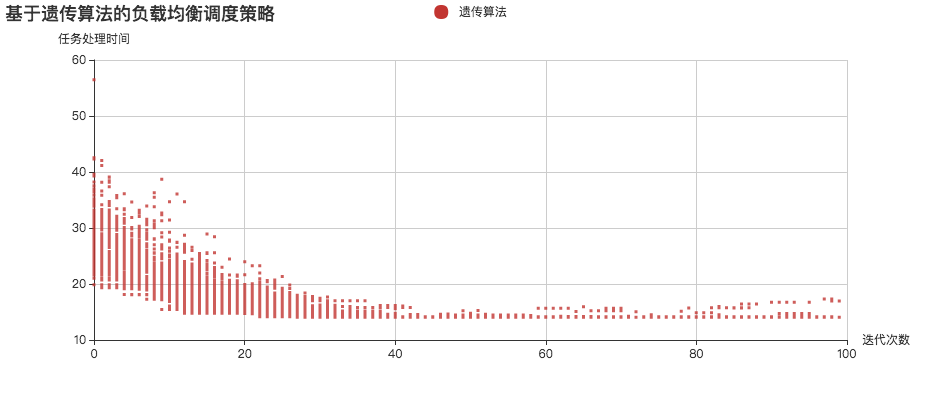
上述演算法一共進行了100次進化，每次進化都會生成100條染色體。圖中的橫座標表示進化次數，而縱座標表示任務執行時間。
從圖中我們可以看到，當進化約20次的時候，演算法漸漸收斂於最優解。

寫在最後

• ga.html：展示的頁面
• GA.js：遺傳演算法的完整程式碼
• common.js：通用的JS程式碼

各位大佬直接開啟ga.html即可檢視演算法執行結果。也歡迎各位關注我的個人公眾號 “大閒人柴毛毛“，不定期分享不正經程式設計師的心路歷程。