1758: [Wc2010]重建計劃

Time Limit: 40 Sec  Memory Limit: 162 MB

Description

Input

第一行包含一個正整數N，表示X國的城市個數. 第二行包含兩個正整數L和U，表示政策要求的第一期重建方案中修建道路數的上下限 接下來的N-1行描述重建小組的原有方案，每行三個正整數Ai,Bi,Vi分別表示道路(Ai,Bi),其價值為Vi 其中城市由1..N進行標號

Output

輸出最大平均估值，保留三位小數

Sample Input

4
2 3
1 2 1
1 3 2
1 4 3

Sample Output

2.500

HINT

N<=100000,1<=L<=U<=N-1,Vi<=1000000 新加資料一組 By leoly,但未重測..2016.9.27

　　　　　　　　-by bzoj https://www.lydsy.com/JudgeOnline/problem.php?id=1758 省選R1雖有些不足之處（D2T1寫炸了，還被卡了一個點的常數），不過基於我那點NOIP分，能苟到這個排名就不錯了，知足吧~~，（SD一直到前50之前都沒有NOIP比我低的......） 於是就來準備R2啦~~ 被大佬安利了一發長鏈剖分 於是就上網找BZOJ的長鏈剖分題 於是就找到了這個 一看就是分數規劃嘛； 套用分數規劃的常用二分解法，考慮怎麼check， check需要找條最長鏈，如果沒有[L,U]的限制，可以直接DP最長鏈（最近怎麼光見到這個） 然而有了這個限制DP大概要N^3，（有N^2做法？？N^2log？？） 所以這個限制怎麼辦呢？ 點分加線段樹應該可以做（nlog^3） (點分加單調佇列應該可以nlog^2？？) 不過今天要用長鏈剖分 考慮在每個點X上，維護子樹中所有點從根出發到這個點的路徑，這樣可以通過N^2列舉每兩條（深度加起來-二倍X深度）符合範圍的路徑來各種作差更新答案 N^2列舉所有點，可以改成N^2列舉所有深度，然後可以用一個下標為深度的線段樹變成NlogN——因為當兩個深度中有一個確定後，另一個的範圍是連續的一段區間 然而這個效率總共是N^2log的，也十分不好的 而且記憶體也開不下，而且維護這個線段樹的複雜度也十分不對 後兩個問題可以考慮用線段樹合併解決， 每個點只有一個深度，所以線段樹合併可以做到維護所有點X的時空複雜度為（NlogN） 剩下的問題是NlogN列舉深度進行N次會變為N^2logN 這個怎麼辦呢？ 注意我們對每個X的子樹的列舉過程： ——把前i-1個兒子的子樹和X合併，然後列舉第i個兒子的子樹中的所有深度在X的線段樹中查詢 這樣可以在不遺漏的前提下儘可能少查詢 但是，對i=1時不應該這麼做， 因為即使列舉第一個兒子的所有深度，所能查到的另一個深度也只有x自己的那一個深度， 所以在i=1時，可以考慮在第一個兒子的線段樹中查詢一個可以和X自己的深度匹配的區間 但是這樣雖然常數可能小一點，但效率還是NlogN的 然而，我們發現，實際上對於每個X而言，都有第一個兒子的對應資訊沒有列舉！！ 理所當然地，我們希望第一個兒子是最大深度最大的那個兒子，這樣可以更快些； 可是，對於複雜度而言，這有什麼用嗎？ 其實這對於複雜度而言十分有用： 這時，我們考慮在列舉所有X的子樹的過程中，每個點對效率的影響 每個點只會在列舉其祖先的子樹時有可能影響效率 我們把這棵樹按照子樹的最大深度而不是子樹大小來剖分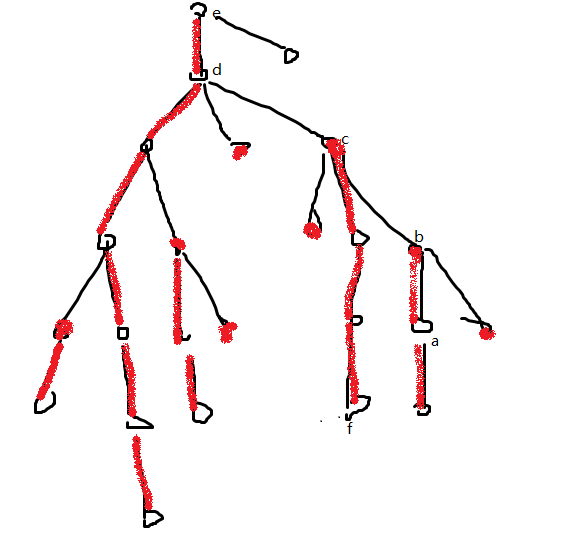

如上圖所示
這時我們發現，每個點a只會在列舉到他所在的重鏈的頂端的父親時對效率造成log的影響

因為：

在列舉a所在的重鏈中的其他祖先節點時，a所在的子樹都是作為深度最深的那個而沒有被列舉（如列舉b的子樹時，a所在的子樹是最深的，沒有被列舉深度）

在列舉更靠上的重鏈內部時，a所在的子樹也是作為深度最深的那個而沒有被列舉(如列舉e的子樹時，a在d這個子樹內，作為最深的存在，沒有被列舉深度)

在列舉更靠上的重鏈頂端的父親時，雖然a所在的子樹需要列舉，但由於我們列舉的是深度，所以因為這個子樹有更深的鏈所以這個效率應該算作那個更深的鏈的效率（如當列舉d的子樹時，儘管a所在的子樹被枚舉了深度，但這個效率應該被算在cf鏈上）

所以這個方法可以做到nlogn

這個“按子樹最大深度剖分樹鏈，對長鏈連結的子節點不做操作”的技巧被稱作一種長鏈剖分

於是我們完美地用$Nlog_2^2N$解決了這個問題

(upd 2018.5.24:不採用線段樹合併，轉而採用基於長鏈剖分的暴力線段樹插入，好像也可以保證效率)

程式碼：

#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
using namespace std;
const LL exp=10000;
const LL INF=1e15;
struct ss{
    int to,next;
    LL val;
}e[200010];
int first[100010],num;
struct DT{
    LL max;
    int ch[2];
}data[3000010];
int root[100010],tot;
int dep[100010],depst[100010],hw[100010];
LL val[100010];
LL l,r,mid,ans;
int n,Low,Top;
void build(int ,int ,LL );
bool check(LL );
void dfs_1(int ,int );
void dfs_2(int );
void insert(int ,int ,int&,int ,LL );
LL get_max(int ,int ,int ,int ,int );
LL get_poi_max(int ,int ,int ,int );
void merge(int ,int ,int ,int&);
int main()
{
    int i,j,k,o;
    scanf("%d",&n);
    scanf("%d%d",&Low,&Top);
    for(i=1;i<n;i++){
        scanf("%d%d%d",&j,&k,&o);
        build(j,k,o*exp),build(k,j,o*exp);
    }
    dfs_1(1,0);
    l=exp,r=1e10,mid=(l+r)>>1ll;
    while(l<r-3){
        if(check(mid))    l=mid;
        else            r=mid-1;
        mid=(l+r)>>1ll;
    }
    for(mid=r;mid>=l;mid--)
        if(check(mid)){
            printf("%.3lf",mid/10000.0);
            return 0;
        }
}
void build(int f,int t,LL v){
    e[++num].next=first[f];
    e[num].to=t,e[num].val=v;
    first[f]=num;
}
bool check(LL lim){
    int i;
    memset(root,0,sizeof(root)),tot=0;
    memset(data,0,sizeof(data)),data[0].max=-3*INF;
    for(i=1;i<=num;i++)    e[i].val-=lim;
    ans=-3e10;
    dfs_2(1);
    for(i=1;i<=num;i++)    e[i].val+=lim;
    return ans>=0;
}
void dfs_1(int now,int fa){
    int i;
    dep[now]=dep[fa]+1;
    depst[now]=dep[now],hw[now]=-1;
    for(i=first[now];i;i=e[i].next)
        if(e[i].to!=fa){
            dfs_1(e[i].to,now);
            if(depst[now]<depst[e[i].to])
                depst[now]=depst[e[i].to],hw[now]=i;
        }
}
void dfs_2(int now){
    int i,j;
    if(hw[now]!=-1){
        val[e[hw[now]].to]=val[now]+e[hw[now]].val;
        dfs_2(e[hw[now]].to);
        root[now]=root[e[hw[now]].to];
        if(dep[now]+Low<=depst[now]);
            ans=max(ans,get_max(1,n,root[now],dep[now]+Low,min(depst[now],dep[now]+Top))-val[now]);
        insert(1,n,root[now],dep[now],val[now]);
    }
    else{
        insert(1,n,root[now],dep[now],val[now]);
        return ;
    }
    for(i=first[now];i;i=e[i].next)
        if(dep[e[i].to]>dep[now]&&i!=hw[now]){
            val[e[i].to]=val[now]+e[i].val;
            dfs_2(e[i].to);
            for(j=dep[e[i].to];j<=depst[e[i].to]&&j<=dep[now]+Top;j++)
                ans=max(ans,get_poi_max(1,n,root[e[i].to],j)-val[now]+get_max(1,n,root[now],max(dep[now]*2+Low-j,dep[now]+1),min(dep[now]*2+Top-j,depst[now]))-val[now]);
            merge(1,n,root[e[i].to],root[now]);
        }
}
void insert(int l,int r,int&now,int lim,LL x){
    if(!now)now=++tot;
    if(l==r){
        data[now].max=x;
        return ;
    }
    int mid=(l+r)>>1;
    if(lim<=mid)
        insert(l,mid,data[now].ch[0],lim,x);
    else
        insert(mid+1,r,data[now].ch[1],lim,x);
    data[now].max=max(data[data[now].ch[0]].max,data[data[now].ch[1]].max);
}
LL get_max(int l,int r,int now,int L,int R){
    if(L>R)return data[0].max;
    if(L<=l&&r<=R)
        return data[now].max;
    int mid=(l+r)>>1;
    LL lm=-INF,rm=-INF;
    if(L<=mid)
        lm=get_max(l,mid,data[now].ch[0],L,R);
    if(R>mid)
        rm=get_max(mid+1,r,data[now].ch[1],L,R);
    if(lm>rm)    return lm;
    return rm;
}
LL get_poi_max(int l,int r,int now,int lim){
    if(l==r)return data[now].max;
    int mid=(l+r)>>1;
    if(lim<=mid)
        return get_poi_max(l,mid,data[now].ch[0],lim);
    else
        return get_poi_max(mid+1,r,data[now].ch[1],lim);
}
void merge(int l,int r,int pre,int&now){
    if(!now||!pre){
        now+=pre;
        return ;
    }
    if(l==r){
        data[now].max=max(data[now].max,data[pre].max);
        return ;
    }
    int mid=(l+r)>>1;
    merge(l,mid,data[pre].ch[0],data[now].ch[0]);
    merge(mid+1,r,data[pre].ch[1],data[now].ch[1]);
    data[now].max=max(data[data[now].ch[0]].max,data[data[now].ch[1]].max);
}

（bzoj卡到39S......）