APOI講了這個東西，還有THU命題的《九省·林克卡特樹》，感覺好像很熱點的樣子。

帶權二分是一類對DP的優化，對於某些最優化問題的(2d/yd)DP，通過這種優化，其效率可以達到簡化後的(1d/yd)DP的效率乘一個log

（(xd/yd)DP是指狀態數為n^x級且每種狀態的轉移數為$n^y$級的DP，這個形式下的DP的最好效率是$n^{x+y}$的）

有這麼一個(2d/yd)DP：

——對於某狀態二元組(i,j),有最優值f[i][j]；

——每個f[i][j]的得出，都需要比較$n^y$個其他的狀態二元組，從中挑出一個可以使f[i][j]更優的狀態作為前驅來進行轉移；

——需要某一個f[n][m]的結果（因為n和m同級，所以可以認為狀態數為$n^2$級）。

考慮優化這個(2d/yd)DP，也就是把它降為一個其他的(x'd/y'd)DP使得x'+y'<2+y

考慮使y減小——

由於在此類DP中，每一個狀態的得出，最終只需要從所有備選的前驅中挑一個來進行轉移，

於是在最理想的情況(也就是經過各種神奇優化之後)，我們可以不經過比較一步找到每個狀態的前驅

這樣就是一個(2d/0d)的DP了，效率$O(n^2)$，

對於決策過程的優化就到此為止了，這一部分並不是本文的重點，所以可以看出，他被一筆帶過了。

現在我們考慮優化狀態數，也就是把2d變成1d——

考慮有一個(2d/yd)DP，我們要得到的是狀態(n,m)的最值f[n][m]

如果這個DP沒有第二位限制的話是一個非常好搞的1dDP(狀態為x時，其答案f'[x]為原來f[x][i]中i列舉所有值時的最優值，由於DP狀態的精確性有所下降，所以一般情況下f'的DP的確可以是一個(1d/y'd)DP，而且y'<=y,也就是一個比之前更好搞的DP)

那我們儘量希望把第二位消掉，以優化狀態數

設有函式F滿足F(i)=f[n][i]；

F在整點處的最值，也是對於所有i而言f[n][i]的最值；

那麼設這個值為f'[n]，可以發現f'[n]就是我們上文中所說的消去第二位限制後出現的那個很好搞的DP

然而，這樣得到的f'[n]=f[n][x]，卻並不能保證x=m。

考慮給F搭配另一個函式G以得到函式H，使得H(x)=F(x)+G(x)

且H(x)在x=m時取得整點處的最值；

這樣的話，設這個最值為h'[n]，如果h'[n]也恰好是個很好搞的(1d/y''d)DP(這需要G十分恰當)，那麼h'[n]就可以是我們優化狀態數的產物。而最終的答案就是h'[n]-G(m)了

帶權二分（斜率凸優化）就是上述討論的一個簡單易行而應用廣泛的特例。

比如有f[a][b]=max(列舉c){f[a-1][c]+val[c+1,b]},

由之前的定義有$F_{max}$=f'[n]=max(列舉i){f[n][i]}

可以發現f'[x]是一個很好搞的DP——

f'[b]=max(列舉c){f'[c]+val[c+1,b]}

如果F的曲線滿足如下圖的凸性：

比如F(x)是下圖這樣的曲線

那麼只要H(x)是F(x)搭配不同斜率的正比例函式G(x)（即H(x)=F(x)+K*x，其中G(x)=K*x），就可以使不同的x變成H(x)取到最值的地方

而且h'[x]也是一個很好搞的DP——

當G的斜率為K時，h'[b]=max(列舉c){h'[c]+val[c+1,b]+K}

(每轉移一次就相當於原來的f中第二位+1，這意味著G的自變數+1,此時G對h'多貢獻了K)

於是剩下的問題就是如何找到一個合適的K，使得H的最優值h'[n]在m處取得了

因為只要K合適，那麼答案就是f[n][m]=h'[n]-m*K，而h'是一個很好搞的DP，於是此類題目就結了。

我們發現由於F函式曲線的凸性，當K逐漸減小時，H的最值取得的位置逐漸右移，

這意味著K可以二分取得：

每次二分一個K’，DP計算當前的h'[n]，並計算當前h'[n]=H(x)的這個x是那一個x

如果這個x>m就blabla

如果這個x<m就blabla

這樣最後會得到了一個合適的K，並同時也就得到問題的答案了。

而對於F的曲線滿足如下圖凸性的情況：

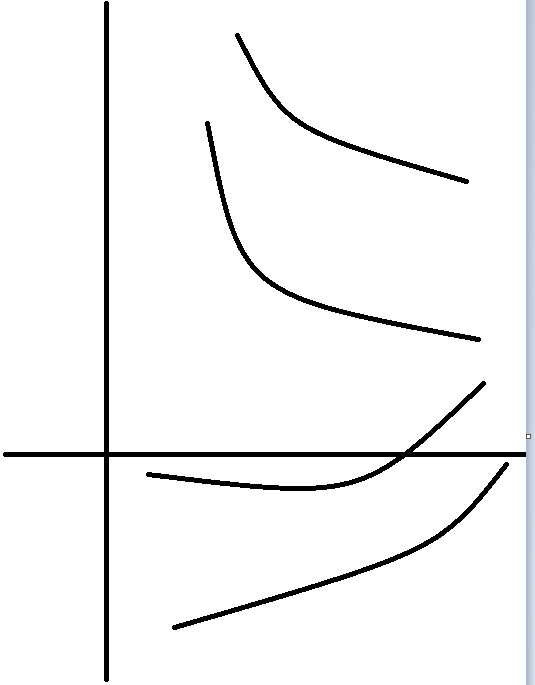
我們可以用同樣的方法，搭配不同斜率的正比例函式G(x)使得H(x)的min值在不同的x處取得。

方法之前的類似。

總結：

對於f[n][m]

如果f[n][m]求解max值

且設F(x)=f[n][x]，有F(x)是隨x增加，斜率遞減的函式

那麼我們可以通過斜率凸優化解決這個問題

如果f[n][m]求解min值

且設F(x)=f[n][x]，有F(x)是隨x增加，斜率增的函式

那麼我們可以通過斜率凸優化解決這個問題

例子：

有如下DP方程——

$$f_{[i][j]}=MIN_{k∈[0,j-1]}f_{[i-1][k]}+(sum_{l=k+1}^{j}a[l])^2$$

$$且對於所有i>j，有f_{[i][j]}=INF$$

其中a[x]為輸入資料

求解$f_{[m][n]}$

可以看出$f_{[m][n]}$為把n個數分成m段，求每段和的平方的和。

設$F(x)=f{[x][n]}$可以證明F(x)是一個隨x增加，斜率增的函式。

如果沒有m段的限制的話

有$f'_{[j]}=MIN_{k∈[0,j-1]}f_{[k]}+(sum_{l=k+1}^{j}a[l])^2$

通過預處理字首和以及一些斜率優化技巧，這個方程可以做到O(n)

如果我們給每次劃分搭配一個費用K的話

就有$h'_{[j]}=MIN_{k∈[0,j-1]}h_{[k]}+(sum_{l=k+1}^{j}a[l])^2+K$

同樣可以斜率優化做到O(n),

這樣，我們二分K，判定此時$h'_{[n]}$對應的劃分次數與m的關係，從而找的一個合適的K，進而找的問題的答案。

最終效率為O(nlogV)