弗洛伊德演算法
2 int i,j,k;
3 for(k=1;k<=n;k++)
4 for(i=1;i<=n;i++)
5 for(j=1;j<=n;j++)
6 if(dist[i][k]+dist[k][j]<dist[i][j])
7 dist[i][j]=dist[i][k]+dist[k][j];
8 }
注意下第6行這個地方，如果dist[i][k]或者dist[k][j]不存在，程式中用一個很大的數代替。最好寫成if(dist[i][k]!=INF && dist[k][j]!=INF && dist[i][k]+dist[k][j]<dist[i][j])，從而防止溢位所造成的錯誤。
上面這個形式的演算法其實是Floyd演算法的精簡版，而真正的Floyd演算法是一種基於DP(Dynamic Programming)的最短路徑演算法。
設圖G中n 個頂點的編號為1到n。令c [i, j, k]表示從i 到j 的最短路徑的長度，其中k 表示該路徑中的最大頂點，也就是說c[i,j,k]這條最短路徑所通過的中間頂點最大不超過k。因此，如果G中包含邊<i, j>，則c[i, j, 0] =邊<i, j> 的長度；若i= j ，則c[i,j,0]=0；如果G中不包含邊<i, j>，則c (i, j, 0)= +∞。c[i, j, n] 則是從i 到j 的最短路徑的長度。
對於任意的k>0，通過分析可以得到：中間頂點不超過k 的i 到j 的最短路徑有兩種可能：該路徑含或不含中間頂點k。若不含，則該路徑長度應為c[i, j, k-1]，否則長度為 c[i, k, k-1] +c [k, j, k-1]。c[i, j, k]可取兩者中的最小值。
狀態轉移方程：c[i, j, k]=min{c[i, j, k-1], c [i, k, k-1]+c [k, j, k-1]}，k＞0。
這樣，問題便具有了最優子結構性質，可以用動態規劃方法來求解。
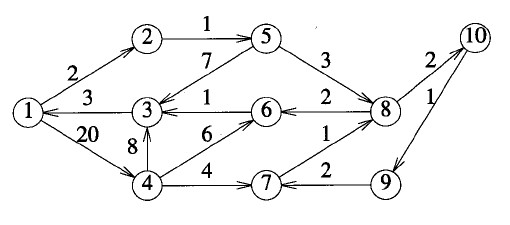為了進一步理解，觀察上面這個有向圖：若k=0, 1, 2, 3，則c[1,3,k]= +∞；c[1,3,4]= 28；若k = 5, 6, 7，則c [1,3,k] = 10；若k=8, 9, 10，則c[1,3,k] = 9。因此1到3的最短路徑長度為9。 下面通過程式來分析這一DP過程，對應上面給出的有向圖：
1 #include <iostream> 2 usingnamespace std;3 4 constint INF =100000;
5 int n=10,map[11][11],dist[11][11][11];
6 void init(){
7 int i,j;
9 for(j=1;j<=n;j++)
10 map[i][j]=(i==j)?0:INF;
11 map[1][2]=2,map[1][4]=20,map[2][5]=1;
12 map[3][1]=3,map[4][3]=8,map[4][6]=6;
13 map[4][7]=4,map[5][3]=7,map[5][8]=3;
14 map[6][3]=1,map[7][8]=1,map[8][6]=2;
15 map[8][10]=2,map[9][7]=2,map[10][9]=1;
16 }
18 int i,j,k;
19 for(i=1;i<=n;i++)
20 for(j=1;j<=n;j++)
21 dist[i][j][0]=map[i][j];
22 for(k=1;k<=n;k++)
23 for(i=1;i<=n;i++)
24 for(j=1;j<=n;j++){
25 dist[i][j][k]=dist[i][j][k-1];
26 if(dist[i][k][k-1]+dist[k][j][k-1]<dist[i][j][k])
27 dist[i][j][k]=dist[i][k][k-1]+dist[k][j][k-1];
28 }
29 }
30 int main(){
31 int k,u,v;
32 init();
33 floyd_dp();
34 while(cin>>u>>v,u||v){
35 for(k=0;k<=n;k++){
36 if(dist[u][v][k]==INF) cout<<"+∞"<<endl;
37 else cout<<dist[u][v][k]<<endl;
38 }
39 }
40 return0;
41 }
輸入 1 3
輸出 +∞
+∞
+∞
+∞
28
10
10
10
9
9
9
Floyd-Warshall演算法不僅能求出任意2點間的最短路徑，還可以儲存最短路徑上經過的節點。下面用精簡版的Floyd演算法實現這一過程，程式中的圖依然對應上面的有向圖。
3 4 constint INF =100000;
5 int n=10,path[11][11],dist[11][11],map[11][11];
6 void init(){
7 int i,j;
8 for(i=1;i<=n;i++)
9 for(j=1;j<=n;j++)
10 map[i][j]=(i==j)?0:INF;
11 map[1][2]=2,map[1][4]=20,map[2][5]=1;
12 map[3][1]=3,map[4][3]=8,map[4][6]=6;
13 map[4][7]=4,map[5][3]=7,map[5][8]=3;
14 map[6][3]=1,map[7][8]=1,map[8][6]=2;
15 map[8][10]=2,map[9][7]=2,map[10][9]=1;
16 }
17 void floyd(){
18 int i,j,k;
19 for(i=1;i<=n;i++)
20 for(j=1;j<=n;j++)
21 dist[i][j]=map[i][j],path[i][j]=0;
22 for(k=1;k<=n;k++)
23 for(i=1;i<=n;i++)
24 for(j=1;j<=n;j++)
25 if(dist[i][k]+dist[k][j]<dist[i][j])
26 dist[i][j]=dist[i][k]+dist[k][j],path[i][j]=k;
27 }
28 void output(int i,int j){
29 if(i==j) return;
30 if(path[i][j]==0) cout<<j<<'';
31 else{
32 output(i,path[i][j]);
33 output(path[i][j],j);
34 }
35 }
36 int main(){
37 int u,v;
38 init();
39 floyd();
40 while(cin>>u>>v,u||v){
41 if(dist[u][v]==INF) cout<<"No path"<<endl;
42 else{
43 cout<<u<<'';
44 output(u,v);
45 cout<<endl;
46 }
47 }
48 return0;
49 }
輸入 1 3
輸出 1 2 5 8 6 3
相關推薦
程式設計基礎26 弗洛伊德演算法
題目描述 在帶權有向圖G中，求G中的任意一對頂點間的最短路徑問題，也是十分常見的一種問題。 解決這個問題的一個方法是執行n次迪傑斯特拉演算法，這樣就可以求出每一對頂點間的最短路徑，執行的時間複雜度為O(n3)。 而另一種演算法是由弗洛伊德提出的，時間複雜度同樣是O(n3)，但演算法的形式
最短路徑-Floyd(弗洛伊德)演算法
最短路徑-Floyd(弗洛伊德)演算法 簡介： 相較Dijkstra，Floyd是一個完全窮舉圖中每個點到末尾點的最短路徑 演算法思想： 按慣例說兩個工具 Path[MAX_SIZE][MAX_SIZE]：儲存所有的最短路徑（指向
拓撲排序以及迪傑斯特拉演算法和弗洛伊德演算法的一些例子（天勤資料結構）
拓撲排序核心演算法 在一個有向圖中找到一個拓撲排序的過程如下： 1）從一個有向圖中選擇一個沒有前驅(入度為0)的頂點輸出； 2）刪除1)中的頂點，並刪除從該頂點出發的全部邊；
最短路徑（鄰接矩陣）（弗洛伊德演算法）
#include<bits/stdc++.h> #define MaxInt 1e8 #define MVNum 100 #define OK 1 #define ERROR 0 using namespace std; typedef int VerTexType; typedef i
結點對最短路徑Floyd弗洛伊德演算法解析
暑假，小哼準備去一些城市旅遊。有些城市之間有公路，有些城市之間則沒有，如下圖。為了節省經費以及方便計劃旅程，小哼希望在出發之前知道任意兩個城市之前的最短路程。 上圖中有4個城市8條公路，公路上的數字表示這條公路的長短。請注意這些公
最短路徑迪傑斯特拉演算法和弗洛伊德演算法實現
迪傑斯特拉演算法： 矩陣二位陣列矩陣T儲存頂點vi到各頂點的最短路徑值，初始狀態為鄰接頂點為弧的權值，非鄰接頂點為無窮大。陣列S用於儲存最短路徑，儲存單元為該弧的前驅頂點的下標和與前驅頂點之間的弧的權值。 1.從T中找出一條弧值最小的弧（vi，vj），將該弧加入S中，並根據vj的鄰接點vx更
資料結構篇：校園最短路徑導航（二：弗洛伊德演算法理解與應用）
求最短路徑最常用的有迪傑斯特拉（Dijkstra）和弗洛伊德（Floyd）演算法兩種。本著簡潔為王道的信條，我選擇了Floyd演算法。 Floyd演算法 首先來看一個簡單圖，紅色標記代表在陣列的下標，橙色標記代表距離（邊權值） 我們用D[6][6]這個矩陣儲存兩點之間最短路徑，
說說弗洛伊德演算法
弗洛伊德演算法，是當時集訓的時候學最短路問題的第一個演算法（去年寒假），當時學長直說這個演算法好寫、時間複雜度高，至於這個演算法是什麼原理卻沒有講。學長說，照著敲就可以，迴圈敲對了，就那麼神奇的對了，迴圈順序錯了，就神奇的WA了。 今年寒假，我也是學長了，逗比碩把最短路給我了，就變成這一週我要
Warshall（弗洛伊德演算法）
簡介：Floyd演算法又稱為插點法，是一種利用動態規劃的思想尋找給定的加權圖中多源點之間最短路徑的演算法，與Dijkstra演算法類似。該演算法名稱以創始人之一、1978年圖靈獎獲得者、斯坦福大學計算機科學系教授羅伯特·弗洛伊德命名。eg：暑假，小哼準備去一些城市旅遊
Floyd algorithm!!!!!（萬惡的弗洛伊德演算法）
曾經有位滑稽的博主說過：搜尋就是優雅的暴力。今天他又要說，DP就是優雅地搜尋。 不是每一個弗洛伊德都寫演算法，也不是寫演算法的都叫弗洛伊德，還有一位人家寫性學三論去了。 這位弗洛伊德來歷不一般，斯坦福大學的教授，1978年的
弗洛伊德演算法-----最短路徑演算法（一）
學習此演算法的原因：昨天下午遛彎的時候，碰到閨蜜正在看演算法，突然問我會不會弗洛伊德演算法？我就順道答應，然後用了半個小時的時間，學習了此演算法，並用5分鐘講解給她聽，在此也分享給各位需要的朋友，讓你們在最短的時間內，透徹的掌握該演算法。 Robert W. Floyd(
C語言弗洛伊德演算法的實現
弗洛伊德演算法和迪傑斯特拉演算法一樣，用於求兩個節點之間的最短路徑，過程也比迪傑斯特拉演算法更為簡單。以下是實現程式碼：首先仍然是預定義和型別定義：#define OK 1 #define ERROR 0 #define Max_Int 37262 #define MVNum
多源最短路徑弗洛伊德演算法（java）不含具體路徑
Floyd-Warshall演算法（Floyd-Warshall algorithm）是解決任意兩點間的最短路徑的一種演算法，可以正確處理有向圖或負權的最短路徑問題。 import java.util.Arrays; public class Florid
Floyd(弗洛伊德)演算法 詳解+模板
弗洛伊德演算法介紹 和Dijkstra演算法一樣，弗洛伊德(Floyd)演算法也是一種用於尋找給定的加權圖中頂點間最短路徑的演算法。該演算法名稱以創始人之一、1978年圖靈獎獲得者、斯坦福大學計算機科學系教授羅伯特·弗洛伊德命名。 基本思想 通過Floyd計算
【原創】求最短路徑-弗洛伊德演算法
有這樣一類題，它要求你從某個點出發，到某個為止走過的最短路徑。當然不會有這種題“從A點出發到B點”。一般來講，是這樣的題目“小明從重慶出發到北京，蘭後可以中轉3個城市，每個城市有1個機場或1條公路連
弗洛伊德演算法
Floyd-Warshall演算法，簡稱Floyd演算法，用於求解任意兩點間的最短距離，時間複雜度為O(n^3)。我們平時所見的Floyd演算法的一般形式如下： 1 void Floyd(){2 int i,j,k;3 for(k=1;k<=n;k++)4 for(i=1;i<=n;i++)5
弗洛伊德演算法求出最短路徑
#include<stdio.h> #include<stdlib.h> typedef int Edgetype;//儲存邊的關係 typedef char VerType;//定點型別應由使用者定義 #define MAXVER 100 #d
六度分離（弗洛伊德演算法）
六度分離Time Limit : 5000/1000ms (Java/Other) Memory Limit : 32768/32768K (Java/Other)Total Submission(s) : 29 Accepted Submission(s) : 10
HDU 1217 Arbitrage(弗洛伊德演算法）
Arbitrage Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 8989 Accepted Subm
Floyd-Warshall（弗洛伊德演算法）
Floyd演算法是用來找出每對頂點之間的最短距離,即適用於多源最短路經，它對圖的要求是,既可以是無向圖也可以是有向圖,邊權可以為負,但是不能存在負環(可根據最小環的正負來判定). 具體可閱讀以下博文： 問題集錦：