【坐在馬桶上看演算法】演算法8：巧妙的鄰接表（陣列實現）

之前我們介紹過圖的鄰接矩陣儲存法，它的空間和時間複雜度都是N2，現在我來介紹另外一種儲存圖的方法：鄰接表，這樣空間和時間複雜度就都是M。對於稀疏圖來說，M要遠遠小於N2。先上資料，如下。

1. 4 5   
2. 1 4 9   
3. 4 3 8   
4. 1 2 5   
5. 2 4 6   
6. 1 3 7 

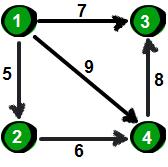
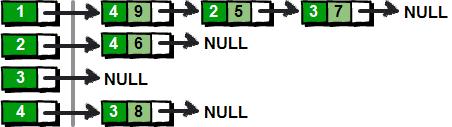
第一行兩個整數n m。n表示頂點個數（頂點編號為1~n），m表示邊的條數。接下來m行表示，每行有3個數x y z，表示頂點x到頂點y的邊的權值為z。下圖就是一種使用連結串列來實現鄰接表的方法。

上面這種實現方法為圖中的每一個頂點（左邊部分）都建立了一個單鏈表（右邊部分）。這樣我們就可以通過遍歷每個頂點的連結串列，從而得到該頂點所有的邊了。使用連結串列來實現鄰接表對於痛恨指標的的朋友來說，這簡直就是噩夢。這裡我將為大家介紹另一種使用陣列來實現的鄰接表，這是一種在實際應用中非常容易實現的方法。這種方法為每個頂點i（i從1~n）也都儲存了一個類似“連結串列”的東西，裡面儲存的是從頂點i出發的所有的邊，具體如下。

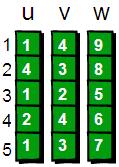
首先我們按照讀入的順序為每一條邊進行編號（1~m）。比如第一條邊“1 4 9”的編號就是1，“1 3 7”這條邊的編號是5。

這裡用u、v和w三個陣列用來記錄每條邊的具體資訊，即u[i]、v[i]和w[i]表示第i條邊是從第u[i]號頂點到v[i]號頂點（u[i]àv[i]），且權值為w[i]。

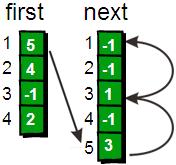
再用一個first陣列來儲存每個頂點其中一條邊的編號。以便待會我們來列舉每個頂點所有的邊（你可能會問：儲存其中一條邊的編號就可以了？不可能吧，每個頂點都需要儲存其所有邊的編號才行吧！甭著急，繼續往下看）。比如1號頂點有一條邊是 “1 4 9”（該條邊的編號是1），那麼就將first[1]的值設為1。如果某個頂點i沒有以該頂點為起始點的邊，則將first[i]的值設為-1。現在我們來看看具體如何操作，初始狀態如下。

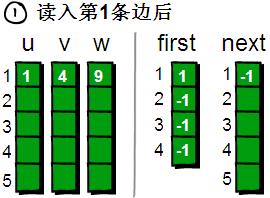
咦？上圖中怎麼多了一個next陣列，有什麼作用呢？不著急，待會再解釋，現在先讀入第一條邊“1 4 9”。

讀入第1條邊（1 4 9），將這條邊的資訊儲存到u[1]、v[1]和w[1]中。同時為這條邊賦予一個編號，因為這條邊是最先讀入的，儲存在u、v和w陣列下標為1的單元格中，因此編號就是1。這條邊的起始點是1號頂點，因此將first[1]的值設為1。

另外這條“編號為1的邊”是以1號頂點（即u[1]）為起始點的第一條邊，所以要將next[1]的值設為-1。也就是說，如果當前這條“編號為i的邊”，是我們發現的以u[i]為起始點的第一條邊，就將next[i]的值設為-1（貌似的這個next陣列很神祕啊⊙_⊙）。

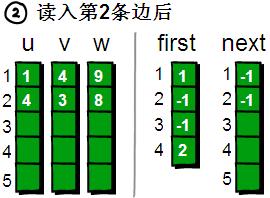
讀入第2條邊（4 3 8），將這條邊的資訊儲存到u[2]、v[2]和w[2]中，這條邊的編號為2。這條邊的起始頂點是4號頂點，因此將first[4]的值設為2。另外這條“編號為2的邊”是我們發現以4號頂點為起始點的第一條邊，所以將next[2]的值設為-1。

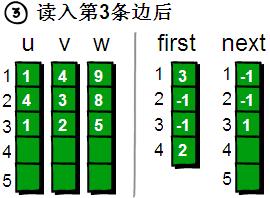
讀入第3條邊（1 2 5），將這條邊的資訊儲存到u[3]、v[3]和w[3]中，這條邊的編號為3，起始頂點是1號頂點。我們發現1號頂點已經有一條“編號為1 的邊”了，如果此時將first[1]的值設為3，那“編號為1的邊”豈不是就丟失了？我有辦法，此時只需將next[3]的值設為1即可。現在你知道next陣列是用來做什麼的吧。next[i]儲存的是“編號為i的邊”的“前一條邊”的編號。

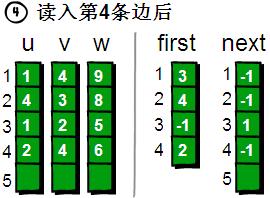
讀入第4條邊（2 4 6），將這條邊的資訊儲存到u[4]、v[4]和w[4]中，這條邊的編號為4，起始頂點是2號頂點，因此將first[2]的值設為4。另外這條“編號為4的邊”是我們發現以2號頂點為起始點的第一條邊，所以將next[4]的值設為-1。

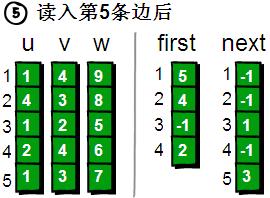
讀入第5條邊（1 3 7），將這條邊的資訊儲存到u[5]、v[5]和w[5]中，這條邊的編號為5，起始頂點又是1號頂點。此時需要將first[1]的值設為5，並將next[5]的值改為3。

此時，如果我們想遍歷1號頂點的每一條邊就很簡單了。1號頂點的其中一條邊的編號儲存在first[1]中。其餘的邊則可以通過next陣列尋找到。請看下圖。

細心的同學會發現，此時遍歷邊某個頂點邊的時候的遍歷順序正好與讀入時候的順序相反。因為在為每個頂點插入邊的時候都直接插入“連結串列”的首部而不是尾部。不過這並不會產生任何問題，這正是這種方法的其妙之處。

建立鄰接表的程式碼如下。

1. int n,m,i;   
2. //u、v和w的陣列大小要根據實際情況來設定，要比m的最大值要大1 
3. int u[6],v[6],w[6];   
4. //first和next的陣列大小要根據實際情況來設定，要比n的最大值要大1 
5. int first[5],next[5];   
6. scanf("%d %d",&n,&m);   
7. //初始化first陣列下標1~n的值為-1，表示1~n頂點暫時都沒有邊 
8. for(i=1;i<=n;i++)   
9.     first[i]=-1;   
10. for(i=1;i<=m;i++)   
11. {   
12.     scanf("%d %d %d",&u[i],&v[i],&w[i]);//讀入每一條邊 
13. //下面兩句是關鍵啦 
14.     next[i]=first[u[i]];   
15.     first[u[i]]=i;   
16. } 

接下來如何遍歷每一條邊呢？我們之前說過其實first陣列儲存的就是每個頂點i（i從1~n）的第一條邊。比如1號頂點的第一條邊是編號為5的邊（1 3 7），2號頂點的第一條邊是編號為4的邊（2 4 6），3號頂點沒有出向邊，4號頂點的第一條邊是編號為2的邊（2 4 6）。那麼如何遍歷1號頂點的每一條邊呢？也很簡單。請看下圖：

遍歷1號頂點所有邊的程式碼如下。

1. k=first[1];// 1號頂點其中的一條邊的編號（其實也是最後讀入的邊） 
2. while(k!=-1) //其餘的邊都可以在next陣列中依次找到 
3. {   
4.     printf("%d %d %d\n",u[k],v[k],w[k]);   
5.     k=next[k];   
6. } 

遍歷每個頂點的所有邊的程式碼如下。

1. for(i=1;i<=n;i++)   
2. {   
3.     k=first[i];   
4. while(k!=-1)   
5.     {   
6.         printf("%d %d %d\n",u[k],v[k],w[k]);   
7.         k=next[k];   
8.     }   
9. } 

可以發現使用鄰接表來儲存圖的時間空間複雜度是O(M)，遍歷每一條邊的時間複雜度是也是O(M)。如果一個圖是稀疏圖的話，M要遠小於N2。因此稀疏圖選用鄰接表來儲存要比鄰接矩陣來儲存要好很多。