動態規劃-凸多邊形最優三角剖分問題
一、 問題描述
多邊形是平面上一條分段線性的閉曲線。也就是說,多邊形是由一系列首尾相接的直線段組成的。組成多邊形的各直線段稱為該多邊形的邊。多邊形相接兩條邊的連線點稱為多邊形的頂點。若多邊形的邊之間除了連線頂點外沒有別的公共點,則稱該多邊形為簡單多邊形。一個簡單多邊形將平面分為3個部分:被包圍在多邊形內的所有點構成了多邊形的內部;多邊形本身構成多邊形的邊界;而平面上其餘的點構成了多邊形的外部。當一個簡單多邊形及其內部構成一個閉凸集時,稱該簡單多邊形為凸多邊形。也就是說凸多邊形邊界上或內部的任意兩點所連成的直線段上所有的點均在該凸多邊形的內部或邊界上。
通常,用多邊形頂點的逆時針序列來表示一個凸多邊形,即P={v0 ,v1 ,… ,vn-1}表示具有n條邊v0v1,v1v2,… ,vn-1vn的一個凸多邊形,其中,約定v0=vn。
若vi與vj是多邊形上不相鄰的兩個頂點,則線段vivj稱為多邊形的一條弦。弦將多邊形分割成凸的兩個子多邊形{vi ,vi+1 ,… ,vj}和{vj ,vj+1 ,… ,vi}。多邊形的三角剖分是一個將多邊形分割成互不相交的三角形的弦的集合T。圖1是一個凸多邊形的兩個不同的三角剖分。
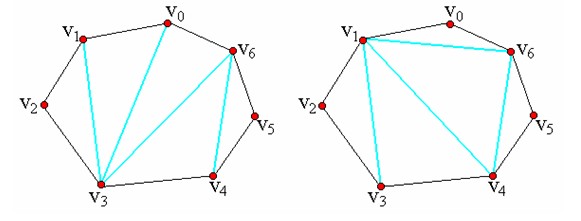
圖1 一個凸多邊形的2個不同的三角剖分
在凸多邊形P的一個三角剖分T中,各弦互不相交,且弦數已達到最大,即P的任一不在T中的弦必與T中某一弦相交。在一個有n個頂點的凸多邊形的三角剖分中,恰好有n-3條弦和n-2個三角形。
凸多邊形最優三角剖分的問題是:給定一個凸多邊形P={v0 ,v1 ,… ,vn-1}以及定義在由多邊形的邊和絃組成的三角形上的權函式ω。要求確定該凸多邊形的一個三角剖分,使得該三角剖分對應的權即剖分中諸三角形上的權之和為最小。
可以定義三角形上各種各樣的權函式ω。例如:定義 ω(vivjvk)=|vivj|+|vivk|+|vkvj|,其中,|vivj|是點vi到vj的歐氏距離。相應於此權函式的最優三角剖分即為最小弦長三角剖分。
二、 演算法思路
凸多邊形的三角剖分與表示式的完全加括號方式之間具有十分緊密的聯絡。正如所看到過的,矩陣連乘積的最優計算次序問題等價於矩陣鏈的完全加括號方式。這些問題之間的相關性可從它們所對應的完全二叉樹的同構性看出。
一個表示式的完全加括號方式對應於一棵完全二叉樹,人們稱這棵二叉樹為表示式的語法樹。例如,與完全加括號的矩陣連乘積((A1(A2A3))(A4(A5A6)))相對應的語法樹如圖2(a)所示。
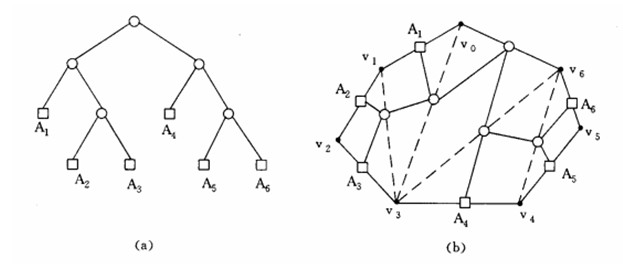
圖2 表示式語法樹與三角剖分的對應
語法樹中每一個葉子表示表示式中一個原子。在語法樹中,若一結點有一個表示表示式E1的左子樹,以及一個表示表示式Er的右子樹,則以該結點為根的子樹表示表示式(E1Er)。因此,有n個原子的完全加括號表示式對應於惟一的一棵有n個葉結點的語法樹,反之亦然。
凸多邊形{v0 ,v1 ,… ,vn-1}的三角剖分也可以用語法樹來表示。例如,圖1(a)中凸多邊形的三角剖分可用圖2(b)所示的語法樹來表示。該語法樹的根結點為邊v0v6,三角剖分中的弦組成其餘的內部結點。多邊形中除v0v6邊外的每一條邊是語法樹的一個葉結點。樹根v0v6是三角形v0v3v6的一條邊,該三角形將原多邊形分為3個部分:三角形v0v3v6,凸多邊形{v0 ,v1 ,… ,v3}和凸多邊形{v3 ,v4 ,… ,v6}。三角形v0v3v6的另外兩條邊,即弦v3v6和v0v3為根的兩個兒子。以它們為根的子樹分別表示凸多邊形{v0 ,v1 ,… ,v3}和凸多邊形{v3 ,v4 ,… ,v6}的三角剖分。
在一般情況下,一個凸n邊形的三角剖分對應於一棵有n-1個葉子的語法樹。反之,也可根據一棵有n-1個葉子的語法樹產生相應的一個凸n邊形的三角剖分。也就是說,凸n邊形的三角剖分與n-1個葉子的語法樹之間存在一一對應關係。由於n個矩陣的完全加括號乘積與n個葉子的語法樹之間存在一一對應關係,因此n個矩陣的完全加括號乘積也與凸(n+1)邊形的三角剖分之間存在一一對應關係。圖2的(a)和(b)表示出了這種對應關係,這時n=6。矩陣連乘積A1A2..A6中的每個矩陣Ai對應於凸(n+1)邊形中的一條邊vi-1vi。三角剖分中的一條弦vivj,i< j,對應於矩陣連乘積A[i+1:j ]。
事實上,矩陣連乘積的最優計算次序問題是凸多邊形最優三角剖分問題的一個特殊情形。 對於給定的矩陣鏈A1A2..An,定義一個與之相應的凸(n+1)邊形P={v0 ,v1 ,… ,vn},使得矩陣Ai與凸多邊形的邊vi-1vi一一對應。若矩陣Ai的維數為pi-1×pi,i=1,2,…,n,則定義三角形vivjvk上的權函式值為: ω(vivjvk)=pipjpk。依此權函式的定義,凸多邊形P的最優三角剖分所對應的語法樹給出矩陣鏈A1A2..An的最優完全加括號方式。
相關推薦
動態規劃-凸多邊形最優三角剖分問題
一、 問題描述 多邊形是平面上一條分段線性的閉曲線。也就是說,多邊形是由一系列首尾相接的直線段組成的。組成多邊形的各直線段稱為該多邊形的邊。多邊形相接兩條邊的連線點稱為多邊形的頂點。若多邊形的邊之間除了連線頂點外沒有別的公共點,則稱該多邊形為簡單多邊形。一個簡
凸多邊形最優三角剖分(演算法設計:動態規劃)
一、動態規劃 和分治法類似,把原問題劃分成若干個子問題,不同的是,分治法(子問題間互相獨立),動態規劃(子問題不獨立) 動態規劃: (1)找出最優解的性質,刻畫其結構特徵 (2)遞迴地定義最優值
動態規劃之凸多邊形最優三角剖分”
問題描述 多邊形是平面上一條分段線性的閉曲線。也就是說,多邊形是由一系列首尾相接的直線段組成的。組成多邊形的各直線段稱為該多邊形的邊。多邊形相接兩條邊的連線點稱為多邊形的頂點。若多邊形的邊之間除了連線頂點外沒有別的公共點,則稱該多邊形為簡單多邊形。一個簡單多邊形將平面分為3個部分:被包圍
凸多邊形最優三角剖分(動態規劃)
#include<stdio.h> #include<stdlib.h> #include<iostream> using namespace std; const int N=7; int Weight(int **w,int a,int b,int c) { r
【動態規劃】凸多邊形最優三角剖分
經典dp問題 1、問題相關定義: (1)凸多邊形的三角剖分:將凸多邊形分割成互不相交的三角形的弦的集合T。 (2)最優剖分:給定凸多邊形P,以及定義在由多邊形的邊和絃組成的三角形上的權函式w。要求確定該凸多邊形的三角剖分,使得該三角剖分中諸三角形上權之和為最小。
0014演算法筆記——【動態規劃】凸多邊形最優三角剖分
1、問題相關定義: (1)凸多邊形的三角剖分:將凸多邊形分割成互不相交的三角形的弦的集合T。 (2)最優剖分:給定凸多邊形P,以及定義在由多邊形的邊和絃組成的三角形上的權函式w。要求確定該凸多邊形的三角剖分,使得該三角剖分中諸三角形上權之和為最小。 凸多邊形三
凸多邊形最優三角剖分的兩種演算法分析
/* Name: Copyright: Author: 巧若拙 Date: 27-03-17 10:11 Description: 動態規劃--凸多邊形最優三角剖分 題目描述: 用多邊形頂點的逆時針序列表示凸多邊形,即P={v0,v1,…,vn
動態規劃 凸 n 邊形三角剖分最小周長
題目輸入凸 n 邊形 p 1 ,p 2 ,··· ,p n , 其中頂點按凸多邊形邊界的逆時針序給出,多邊形中不相鄰頂點間的連線稱為弦。試設計一個動態規劃演算法,用若干條弦將凸邊形 p 1 ,p 2 ,··· ,p n 剖分成一些無公共區域的三角形,使得所有三角形的周長之和最
zoj 3537 Cake 【凸包 + 區間dp】 【最優三角剖分】
Cake Time Limit: 1 Second Memory Limit: 32768 KB You want to hold a party. Here's a polygon-shaped cake on the table. You'd like t
最優三角剖分
return min std esp div 技術分享 include %d logs 同樣是紫書上的題。 紫書上並沒有給出每一個三角形所貢獻的的權值的計算方法,我這裏就擅作主張,定義成點權的乘積和好了。 那麽做法是DP,這裏註意設狀態的方式(我這麽設是為了使需要求解的問題
經典問題四. 【區間dp】 凸多邊形最優三角形劃分
(區間dp) 凸多邊形最優三角形劃分 問題描述: 思路: 將凸多邊形的點陣列化。發現三角形劃分是滿足區間疊加的。 dp[i][j],1<=i<=j<=N,代表凸子多邊形{v
動態規劃7:最優編輯練習題
題目:對於兩個字串A和B,我們需要進行插入、刪除和修改操作將A串變為B串,定義c0,c1,c2分別為三種操作的代價,請設計一個高效演算法,求出將A串變為B串所需要的最少代價。給定兩個字串A和B,及它們的長度和三種操作代價,請返回將A串變為B串所需要的最小代價。保證兩串長度均
動態規劃-凸多邊形
時間限制:10000ms 單點時限:1000ms 記憶體限制:256MB 描述 給定一個凸多邊形的N個頂點。你需要在凸多邊形內找到M個點,使得這M個點也圍成一個凸多邊形,並且圍成的面積儘可能大
2018.09.30【POJ3348】Cows(凸包)(三角剖分)
傳送門 解析: 讀優沒有寫負數又被卡了半個小時。。。 這裡採用JarrisJarrisJarris步進法求凸包。。主要講一講怎麼求多邊形面積。 思路: 滿足題意的顯然是這些點的凸包,而我們要做的就是求出凸包面積。 那麼怎麼求多邊形面積? 考慮三角剖分,我們將多
最優三角形剖分
//此演算法和演算法導論上的矩陣鏈乘法的演算法一樣,稍微有點修改 #include<iostream> #include<fstream> #include<cmath> #include<cstdlib> using nam
最優三角劃分(動態規劃) By ACReaper
1.有狀態轉移方程為f(i,j) = max(f(i,k) + f(k,j) + w(i,j,k));f(i,j)表示從vi到vj的簡單通路(我們預設vj指向vi),這樣才能構成凸多邊形,同時表示在這個凸多邊形中權和的最大值。 2.由3邊的凸多邊形也就是三角形開始遞推
【動態規劃】UVa 1331 最大面積最小三角形剖分
題目 請點選 題目大意 將一個多邊形用它不相交的對角線將它分成若干個三角形,使得最大的三角形面積最小,求最大三角形的面積。如圖是一個六邊形的幾種剖分: 思路 記由點u,u+1,…,v-1,v(u< v)組成的多邊形為F(i,j) 首
#動態規劃 LeetCode 64 最小路徑和
bsp length 位置 根據 說明 font span 輸入 思考 給定一個包含非負整數的 m x n 網格,請找出一條從左上角到右下角的路徑,使得路徑上的數字總和為最小。 說明:每次只能向下或者向右移動一步。 示例: 輸入: [ [1,3,1], [1,5,1
[SDOI2017]新生舞會,洛谷P3705,分數規劃+二分圖最優匹配
正題 題目連結點這裡 給出兩個矩陣a,b,都表示i和j之間的權值,要求構造一個排列P,使得最大。 我們來二分一個mid,使得,然後變形金剛,
圖論動態規劃演算法——Floyd最短路徑
前言 推出一個新系列,《看圖輕鬆理解資料結構和演算法》,主要使用圖片來描述常見的資料結構和演算法,輕鬆閱讀並理解掌握。本系列包括各種堆、各種佇列、各種列表、各種樹、各種圖、各種排序等等幾十篇的樣子。 Floyd演算法 Floyd是一種經典的多源最短路徑演算法,它通過動態規劃的思想來尋找給定加權圖中的多源
