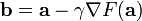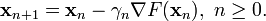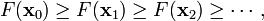線性迴歸 最小二乘 梯度下降 隨機梯度下降
一下午只弄清楚這一個問題了,記錄一下,有點亂:
先從線性迴歸問題說起,為了對樣本點進行擬合求得擬合函式來進行對新的輸入做出預測,便設計了一個衡量擬合函式好壞的標準,其實標準有很多:可以是SUM{|f(Xi) - Yi|} / N; 也可以是SUM{|f(Xi) - Yi|^2} / N;
因為對於不同的擬合函式,樣本點是相同的,那N就是一樣的,所以可以直接比較:
1.SUM{|f(Xi) - Yi|}
或者
2.SUM{|f(Xi) - Yi|^2}
那麼再說說為什麼都比較喜歡用SUM{|f(Xi) - Yi|^2}呢?為什麼都喜歡用平方呢?我看到過兩種殊途同歸的解釋,大概是這樣子的:
一、根據最大似然估計來解釋:
最大似然估計的思想是尋找一種分佈,使得當前樣本出現的概率最大!
這個樣本出現的概率可以表示成各個樣本出現的概率的乘積,當然可以取個對數,變成logP的加和。
接著我們做一個假設:
假設當前樣本服從的那個真實的分佈函式為F(X),在點Xi處取樣得到的樣本服從以F(Xi)為均值的正態分佈(因為有噪聲,否則就應該是準確的F(Xi)而不會有偏差了),我們可以先不考慮珍這個正態分佈的方差,但假設各個點取樣服從的正態分佈的方差是相同的。
先不爭論這樣的假設是否合理,具體我也不知道合理不合理,只是感覺還算合理!
在這樣的假設前提下,樣本點<Xi, Yi>出現的概率正比於Exp(-(Yi-F(Xi))^2),這個就是根據正態分佈的密度函式而來的,具體不要糾結於準確的形式,主要是看那個差的平方。
用你給出現擬合函式f(x)替代這裡的真正的分佈函式F(X),依照最大似然估計的思想就是讓Exp(-SUM{|f(Xi) - Yi|^2})取得最大值。這樣就可以解釋為什麼要用最小二乘的形式來作為衡量擬合函式的標準的原因了吧!
二、根據貝葉斯理論
給出一個擬合函式,評價好壞的標準是根據樣本的後驗概率來裁決;這個感覺跟最大似然估計很像啊。關於樣本分佈做出的假設與前面是一樣的,那後驗概率的公式是什麼呢?是這樣的:P(h|D) ∝ P(h) * P(D|h)
這裡的h指的是擬合函式,D指的是樣本點,那正比式子的右邊是擬合函式的先驗概率乘以該擬合函式得出該樣本點的概率,左邊就是對應的後驗概率了,就是根據樣本點得出目標函式的概率。而各個擬合函式的先驗概率是P(h)是相同的,誰也不比誰更好!所以只用看P(D|h)就可以了,而根據前面做出的假設,這個條件概率也是正比於Exp(-(Yi-F(Xi))^2)的。考慮全部的樣本點,整體的後驗概率是各個樣本點的概率的乘積,就又回到了Exp(-SUM{|f(Xi)
- Yi|^2})這個式子上去了~~~~
回來說這個最小二乘的問題怎麼解呢?如何求得它的最小值呢?可以直接對各個引數求導數,令導數等於0,聯立解方程組!
這就是標準最小二乘法的解法,會得到目標函式的一個解析解,關於這個解析解是怎麼解出來的,我目前還不知道,只是看到結果裡需要對矩陣求逆。標準解法的效率比較低,因為涉及到矩陣運算,計算量太大,所以轉而用梯度下降法來解,在介紹梯度下降法之前,先說明,因為最小二乘問題是一個求凸函式極值的問題,它只有一個最優解,沒有所謂的區域性最優,所以在這個問題上完全可以大膽放心的用梯度下降來解,一開始這裡我一直沒有想明白,因為網上很多介紹梯度下降的總是說不保證全域性最優,他們說的沒錯,但在這個問題上不會出現。
關於梯度下降法、隨機梯度下降法、批量梯度下降法:
一、梯度gradient
在標量場f中的一點處存在一個向量G,該向量方向為f在該點處變化率最大的方向,其模也等於這個最大變化率的數值,則向量G稱為標量場f的梯度。
標量場中某一點上的梯度指向標量場增長最快的方向,梯度的長度是這個最大的變化率。
更嚴格的說,從歐氏空間Rn到R的函式的梯度是在Rn某一點最佳的線性近似。在這個意義上,梯度是雅戈比矩陣的一個特殊情況。
在單變數的實值函式的情況,梯度只是導數,或者,對於一個線性函式,也就是線的斜率。
梯度一詞有時用於斜度,也就是一個曲面沿著給定方向的傾斜程度。
一個標量函式 的梯度記為:
的梯度記為: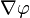 或
或  ,
其中
,
其中 (nabla)表示向量微分運算元。
(nabla)表示向量微分運算元。
二、梯度下降法
梯度下降法,基於這樣的觀察:
如果實值函式  在點
在點  處可微且有定義,那麼函式
處可微且有定義,那麼函式  在
在  點沿著梯度相反的方向
點沿著梯度相反的方向  下降最快。因而,如果
下降最快。因而,如果
對於  為一個夠小數值時成立,那麼
為一個夠小數值時成立,那麼 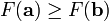 。
。
 是向量。
是向量。
考慮到這一點,我們可以從函式  的區域性極小值的初始估計
的區域性極小值的初始估計  出發,並考慮如下序列
出發,並考慮如下序列 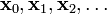 使得
使得
因此可得到
如果順利的話序列 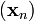 收斂到期望的極值。注意每次迭代步長
收斂到期望的極值。注意每次迭代步長  可以改變。
可以改變。
梯度下降法的缺點是:
- 靠近極小值時速度減慢。
- 直線搜尋可能會產生一些問題。
- 可能會'之字型'地下降。
三、隨機梯度下降法stochastic gradient descent,也叫增量梯度下降
由於梯度下降法收斂速度慢,而隨機梯度下降法會快很多
–根據某個單獨樣例的誤差增量計算權值更新,得到近似的梯度下降搜尋(隨機取一個樣例)
–可以看作為每個單獨的訓練樣例定義不同的誤差函式
–在迭代所有訓練樣例時,這些權值更新的序列給出了對於原來誤差函式的梯度下降的一個合理近似
–通過使下降速率的值足夠小,可以使隨機梯度下降以任意程度接近於真實梯度下降
•標準梯度下降和隨機梯度下降之間的關鍵區別
–標準梯度下降是在權值更新前對所有樣例彙總誤差,而隨機梯度下降的權值是通過考查某個訓練樣例來更新的
–在標準梯度下降中,權值更新的每一步對多個樣例求和,需要更多的計算
–標準梯度下降,由於使用真正的梯度,標準梯度下降對於每一次權值更新經常使用比隨機梯度下降大的步長
–如果標準誤差曲面有多個區域性極小值,隨機梯度下降有時可能避免陷入這些區域性極小值中(此處沒有這種情況出現)
梯度下降演算法是利用梯度下降的方向迭代尋找目標函式的引數的最優值。

它遵循LMS(Least Mean Square是)準則,該準則是通過使似然函式最大推導得出,即得出的引數使得樣本資料集出現的概率最大。
常用的迭代方法有兩種:批量梯度下降法(Batch Gradient Descent)和隨機梯度下降法(Stochastic Gradient Descent)。
批量梯度下降是一種對引數的update進行累積,然後批量更新的一種方式。用於在已知整個訓練集時的一種訓練方式,但對於大規模資料並不合適。
隨機梯度下降是一種對引數隨著樣本訓練,一個一個的及時update的方式。常用於大規模訓練集,當往往容易收斂到區域性最優解。
批量梯度下降法(Batch Gradient Descent):

隨機梯度下降法(Stochastic Gradient Descent):

梯度下降演算法對區域性極值敏感,但是對於線性迴歸問題只有整體極值,沒有區域性極值,所以在這種情況下,演算法總是收斂的。
對於隨機梯度下降演算法,其收斂速度要快於批量梯度下降演算法,但是它在最小值附近震盪的幅度較大,所以可能不會收斂於true minimum。
再補充一個關於批處理梯度下降、隨機梯度下降、mini梯度下降、average梯度下降的簡介
http://blog.sina.com.cn/s/blog_eb3aea990101e6p8.html
寫的挺好的!
相關推薦
線性迴歸 最小二乘 梯度下降 隨機梯度下降
一下午只弄清楚這一個問題了,記錄一下,有點亂: 先從線性迴歸問題說起,為了對樣本點進行擬合求得擬合函式來進行對新的輸入做出預測,便設計了一個衡量擬合函式好壞的標準,其實標準有很多:可以是SUM{|f(Xi) - Yi|} / N; 也可以是SUM{|f(Xi) - Yi|^
簡單線性迴歸-最小二乘法推導過程
最近學習線性迴歸,自己推導了一下最小二乘法。 其他參考文章: https://blog.csdn.net/chasdmeng/article/details/38869941?utm_source=blogxgwz0 https://blog.csdn.net/iter
線性迴歸-最小二乘方法程式碼實現
線性迴歸-最小二乘方法 使用最小二乘的方法進行原始的計算方式編寫 先把該匯入的包全部匯入了 # 首先需要匯入對應的包 import pandas as pd # 資料處理 import numpy as np # 資料計算 import matplotlib.pyplot a
邏輯迴歸、線性迴歸、最小二乘、極大似然、梯度下降
轉自 http://www.zhihu.com/question/24900876 機器學習的基本框架大都是模型、目標和演算法! 重要的事情說三遍! 對於一個數據集,首先你要根據資料的特點和目的來選擇合適模型。 就你問的而言,選定的模型是Logistic Regressi
【機器學習詳解】線性迴歸、梯度下降、最小二乘的幾何和概率解釋
線性迴歸 即線性擬合,給定N個樣本資料(x1,y1),(x2,y2)....(xN,yN)其中xi為輸入向量,yi表示目標值,即想要預測的值。採用曲線擬合方式,找到最佳的函式曲線來逼近原始資料。通過使得代價函式最小來決定函式引數值。 採用斯坦福大學公開課的
機器學習---用python實現最小二乘線性回歸並用隨機梯度下降法求解 (Machine Learning Least Squares Linear Regression Application SGD)
lin python get stat linspace oms mach 實現 all 在《機器學習---線性回歸(Machine Learning Linear Regression)》一文中,我們主要介紹了最小二乘線性回歸模型以及簡單地介紹了梯度下降法。現在,讓我們來
2018.08.28 ali 梯度下降法實現最小二乘
4.3 div 數量 ask pre oss 找到 1.7 二維 - 要理解梯度下降和牛頓叠代法的區別 #include<stdio.h> // 1. 線性多維函數原型是 y = f(x1,x2,x3) = a * x1 + b * x2 + c * x
Andrew Ng機器學習筆記2——梯度下降法and最小二乘擬合
今天正式開始學習機器學習的演算法,老師首先舉了一個例項:已知某地區的房屋面積與價格的一個數據集,那麼如何預測給定房屋面積的價格呢?我們大部分人可以想到的就是將畫出房屋面積與價格的散點圖,然後擬合出價格關於面積的曲線,那麼對於一個已知的房屋面積,就可以在擬合的曲線上得到預測的
牛頓法求解最小二乘問題(線性迴歸)
用牛頓法求解代價函式的最小值,這裡是n維向量,是實數。 解 牛頓法(詳細點此)迭代公式為, 這裡,是關於的偏導數向量;是一個n x n被稱作Hessian的矩陣,其元素為。 先求關於的偏導數 上式
概率統計與機器學習:獨立同分布,極大似然估計,線性最小二乘迴歸
獨立同分布 獨立性 概念:事件A,B發生互不影響 公式:P(XY)=P(X)P(Y) , 即事件的概率等於各自事件概率的乘積 舉例: 正例:兩個人同時向上拋硬幣,兩個硬幣均為正面的概率 反例:獅子在某地區出現的概率為X,老虎出現概率為Y,同時出現
機器學習中最小二乘和梯度下降法的個人理解
提前說明一下,這裡不涉及數學公式的推到,只是根據自己的理解來概括一下,有不準確的地方,歡迎指出。最小二乘:我們通常是根據一些離散的點來擬合出一天直線,這條直線也就是我們所說的模型,最小二乘也就是評價損失函式(loss)的一個指標。最小二乘就是那些離散的點與模型上擬合出的點做一
線性最小二乘兩種方法
梯度下降 神經網絡 log des sum 直線 ini 結束 erro 線性最小二乘擬合 y = w0 +w1x (參數 w0, w1) (1)如何評價一條擬合好的直線 y = w0 +w1x 的誤差? "cost" of a given line : Res
MIT線性代數:16.投影矩陣和最小二乘
線性代數 技術 最小二乘 最小 image 代數 線性 圖片 投影 MIT線性代數:16.投影矩陣和最小二乘
線性代數筆記18——投影矩陣和最小二乘
一維空間的投影矩陣 先來看一維空間內向量的投影: 向量p是b在a上的投影,也稱為b在a上的分量,可以用b乘以a方向的單位向量來計算,現在,我們打算嘗試用更“貼近”線性代數的方式表達。 因為p趴在a上,所以p實際上是a的一個子空間,可以將它看作a放縮x倍,因此向量p可以用p = xa來表示
最小二乘迴歸,嶺迴歸,Lasso迴歸,彈性網路
普通最小二乘法 理論: 損失函式: 權重計算: 1、對於普通最小二乘的係數估計問題,其依賴於模型各項的相互獨立性。 2、當各項是相關的,且設計矩陣 X的各列近似線性相關,那麼,設計矩陣會趨向於奇異矩陣,這會導致最小二乘估計對於隨機誤差非常敏感
線性代數之——最小二乘
1. 最小二乘 A x = b
求解線性最小二乘系統
一個超定方程組,比如Ax = b,沒有解。 在這種情況下,在差值Ax-b儘可能小的意義上,搜尋最接近解的向量x是有意義的。 這個x被稱為最小二乘解(如果使用歐幾里德範數)。本頁討論的三種方法是SVD分解,QR分解和正規方程。 其中,SVD分解通常是最準確的,但最慢的正規方程是
Python實現-----使用隨機梯度演算法對高斯核模型進行最小二乘學習法
(1)高斯核模型 其中為樣本。可以看出,核模型的均值是以的元素進行計算的。 (2)隨機梯度下降法 (3)python 程式碼實現 import numpy as np import matplotlib
偏最小二乘迴歸(PLSR)演算法原理
1、問題的提出 在跨媒體檢索領域中,CCA(Canonical correlation analysis,典型關聯分析)是應用最為廣泛的演算法之一。CCA可以把兩種媒體的原始特徵空間對映對映到相關的兩個特徵子空間中,從而實現兩個屬於不同媒體的樣本之間的相似
偏最小二乘(pls)迴歸分析 matlab
偏最小二乘用於查詢兩個矩陣(X和Y)的基本關係,即一個在這兩個空間對協方差結構建模的隱變數方法。偏最小二乘模型將試圖找到X空間的多維方向來解釋Y空間方差最大的多維方向。偏最小二乘迴歸特別適合當預測矩陣比觀測的有更多變數,以及X的值中有多重共線性的時候。通過投影預測變數和觀測變