排序（Sorting）是計算機內經常進行的一種操作，其目的是將一組“無序”的記錄序列調整為按關鍵字“有序”的記錄序列。如何進行排序，特別是高效率地進行排序時計算機工作者學習和研究的重要課題之一。排序有內部排序和外部排序之分，若整個排序過程不需要訪問外存便能完成，則稱此類排序為內部排序，反之則為外部排序。本篇主要介紹插入排序、交換排序、選擇排序和歸併排序這幾種內部排序方法。

首先，我們今天的目標就是編寫一個SortingHelper類，它是一個提供了多種排序方法的幫助類，後面我們的目標就是實現其中的各種排序靜態方法：

    public static class SortingHelper<T> where
 
 T : IComparable
    {
        public static void StraightInsertSort(T[] arr)
        {
        } 

        public static void ShellSort(T[] arr)
        {
        }

        public static void BubbleSort(T[] arr)
        {
        }

        public static void QuickSort(T[] arr)
        {
        }

        
 
public static void SimpleSelectSort(T[] arr)
        {
        }

        public static void HeapSort(T[] arr)
        {
        }

        public static void MergeSort(T[] arr)
        {
        }
    }

一、插入類排序

　　插入排序（Insertion Sort）的主要思想是不斷地將待排序的元素插入到有序序列中，是有序序列不斷地擴大，直至所有元素都被插入到有序序列中

1.1 直接插入排序

　　直接插入排序（Straight Insertion Sort）的基本操作是將一個記錄插入到已經排好序的有序表中，從而得到一個新的、記錄數增1的有序表。

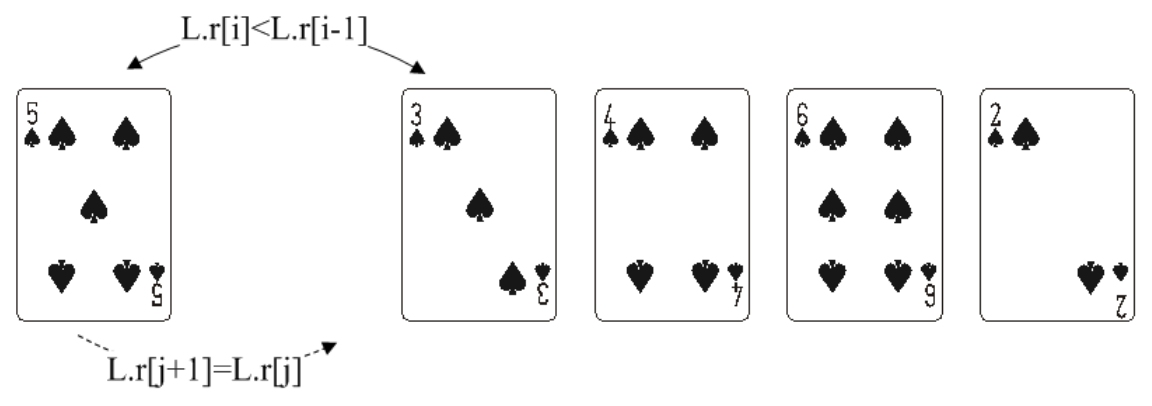
    public static void StraightInsertSort(T[] arr)
    {
        int i, j;
        T temp;

        for (i = 1; i < arr.Length; i++)
        {
            j = i - 1;
            temp = arr[i];

            while (j >= 0 && temp.CompareTo(arr[j]) < 0)
            {
                arr[j + 1] = arr[j];
                j--;
            }

            arr[j + 1] = temp;
        }
    } 

　　通過初始化10000個隨機數的陣列傳入進行測試，藉助CodeTimer類進行效能計數的結果如下圖所示：

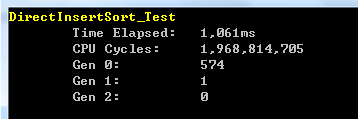
　　排序後的陣列結果如下圖所示，後面的排序結果就不再一一展示了：

　　以上程式碼中，while迴圈條件中j>=0用於避免向前查詢合適位置而導致j值超出陣列界限，這使得每次while迴圈都要進行兩次比較，可以通過設定監哨來對該演算法進行改進，以減少迴圈中的比較次數。所謂監哨就是利用陣列的某個元素來存放當前待排序記錄，從而達到避免陣列越界和減少比較次數的目的。這裡使用arr[0]來作為監哨，改進後的程式碼如下：

    public static void StraightInsertSortWithSentry
    (T[] arr)
    {
        int i, j;

        for (i = 1; i < arr.Length; i++)
        {
            j = i - 1;
            arr[0] = arr[i]; // 將插入元素存放於監哨arr[0]中

            while (arr[0].CompareTo(arr[j]) < 0)
            {
                arr[j + 1] = arr[j]; // 移動記錄
                j--;
            }

            arr[j + 1] = arr[0]; // 將插入元素插入到合適的位置
        }
    }

　　使用監哨的前提是arr[0]元素必須不在待排序序列中，否則在排序前需要在arr[0]處插入一個額外元素，這樣會使陣列中所有元素向右移動一位。

　　總結：直接插入排序最好情況時間複雜度為O(n)，最壞情況下（逆序表）時間複雜度為O(n²)，因此它只適合於資料量較少的情況使用。

1.2 希爾排序

　　希爾排序是D.L.Shell於1959年提出來的一種排序演算法，在這之前排序演算法的時間複雜度基本都是O(n*n)的，希爾排序演算法是突破這個時間複雜度的第一批演算法之一，它是直接插入排序的升級版。希爾排序的基本思想是：將待排序的記錄分成幾組，從而減少參與直接插入排序的資料量，當經過幾次分組之後，記錄的排列已經基本有序，這時再對所有記錄實施直接插入排序。

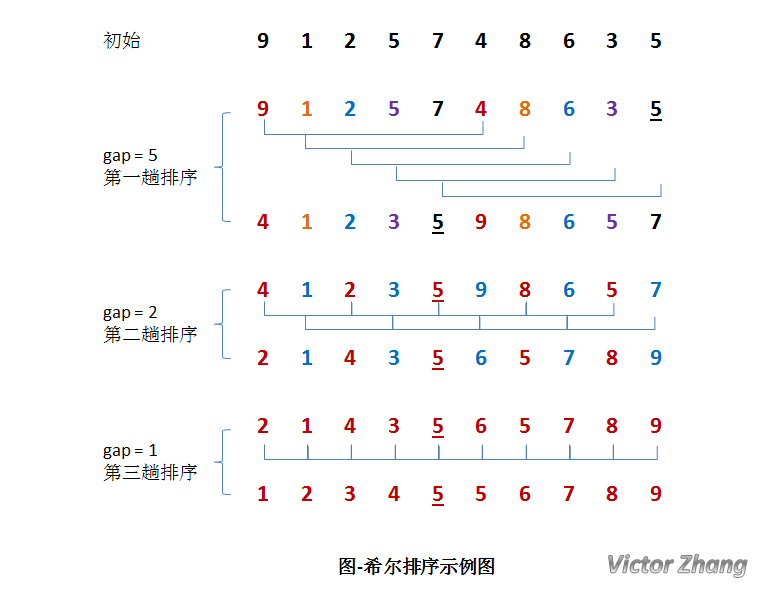
　　希爾排序的主要特點是排序的每一趟均以不同的間隔數對子序列進行排序，當間隔數很大時，被移動的元素是以跳躍式進行的。而當間隔數=1時，序列則幾乎已經有序，只需要進行很少的元素移動，就能最終達到排序的目的。

    public static void ShellSort(T[] arr)
    {
        int i, j, d;
        T temp;

        for (d = arr.Length / 2; d >= 1; d = d / 2)
        {
            for (i = d; i < arr.Length; i++)
            {
                j = i - d;
                temp = arr[i];

                while (j >= 0 && temp.CompareTo(arr[j]) < 0)
                {
                    arr[j + d] = arr[j];
                    j = j - d;
                }

                arr[j + d] = temp;
            }
        }
    }

　　在10000個隨機數的陣列中測試的效能結果如下圖所示：

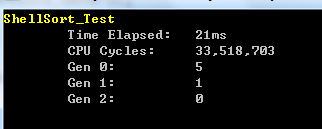
　　總結：Shell排序適用於待排序記錄數量較大的情況，在此情況下，Shell排序一般要比直接插入排序要快（從直接插入排序結果的1061ms到希爾排序的21ms）。1971年，斯坦福大學的兩位教授在大量實驗的基礎上推匯出Shell排序的時間複雜度約為O(n^1.3)，使得我們終於突破了慢速排序的時代（超越了時間複雜度為O(n²)）。

二、交換類排序

　　交換排序（Exchange Sort）的主要思路就是在排序過程中，通過對待排序記錄序列中的元素進行比較，如果發現次序相反，就將儲存位置交換來達到排序目的。

2.1 氣泡排序

　　氣泡排序（Bubble Sort）是一種簡單的交換排序方法，其基本思想是：兩兩比較相鄰記錄的關鍵字，如果反序則交換，直到沒有反序的記錄為止。

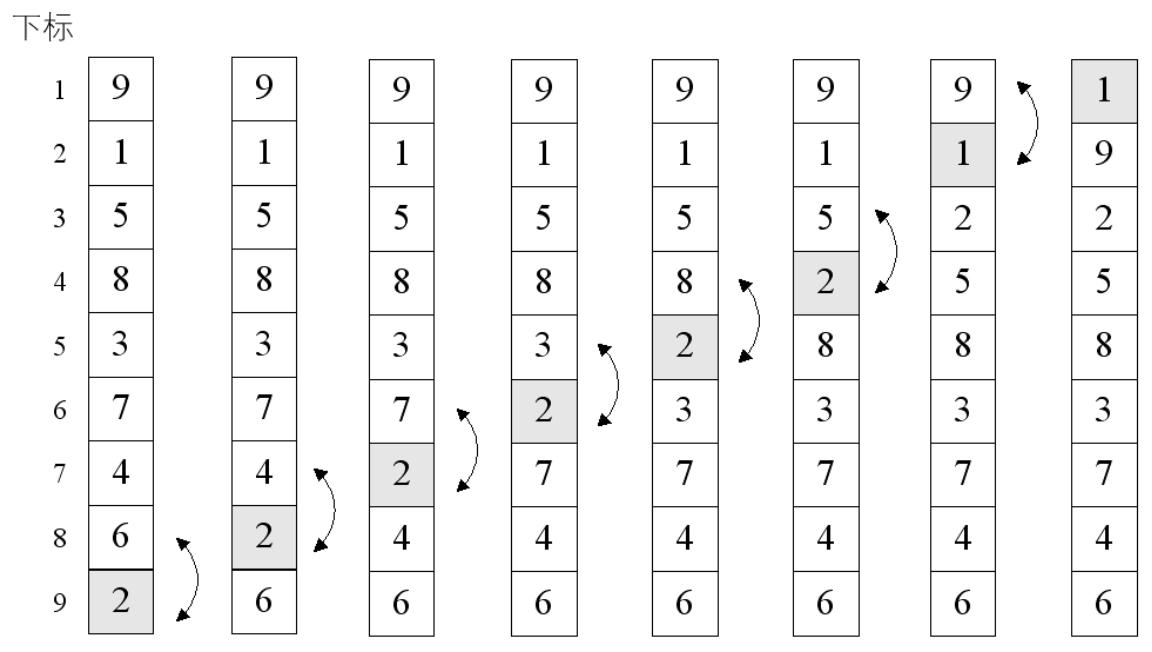
    public static void BubbleSort(T[] arr)
    {
        int i, j;
        T temp;

        for (j = 1; j < arr.Length; j++)
        {
            for (i = 0; i < arr.Length - j; i++)
            {
                if (arr[i].CompareTo(arr[i + 1]) > 0)
                {
                    // 核心操作：交換兩個元素
                    temp = arr[i];
                    arr[i] = arr[i + 1];
                    arr[i + 1] = temp;
                }
            }
        }
    }

　　在10000個隨機數的陣列中測試的效能結果如下圖所示：

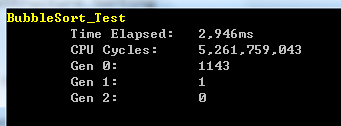
　　從上圖可以看出，氣泡排序對於無序待排序陣列的耗時接近了3秒鐘，垃圾回收次數更是達到了1143次左右。另外，上面的程式碼對於接近有序的待排序陣列的處理效率不高，需要避免因已經有序的情況下的無意義迴圈判斷，因此可以進行如下的改進：

    public static void BubbleSort(T[] arr)
    {
        int i, j;
        T temp;
        bool isExchanged = true;

        for (j = 1; j < arr.Length && isExchanged; j++)
        {
            isExchanged = false;
            for (i = 0; i < arr.Length - j; i++)
            {
                if (arr[i].CompareTo(arr[i + 1]) > 0)
                {
                    // 核心操作：交換兩個元素
                    temp = arr[i];
                    arr[i] = arr[i + 1];
                    arr[i + 1] = temp;
                    // 附加操作：改變標誌
                    isExchanged = true;
                }
            }
        }
    }

　　總結：氣泡排序在執行時間方面，待排序的記錄越接近有序，演算法的執行效率就越高，反之，執行效率則越低，它的平均時間複雜度為O(n²)。

2.2 快速排序

　　氣泡排序在掃描過程中只對相鄰的兩個元素進行比較，因此在互換兩個相鄰元素時只能消除一個逆序。如果通過兩個不相鄰元素的交換能夠消除待排序記錄中的多個逆序，則會大大加快排序的速度。快速排序（Quick Sort）正是通過不相鄰元素交換而消除多個逆序的，因而可以認為其是氣泡排序的升級版。

　　快速排序是由C.A.R Hoare提出並命名的一種排序方法，在目前各種排序方法中，這種方法對元素進行比較的次數較少，因而速度也比較快，被認為是目前最好的排序方法之一。在.NET中的多個集合類所提供的Sort()方法中都使用了快速排序對集合中的元素進行排序。

　　快速排序的基本思想是：通過一趟排序將待排記錄分割成獨立的兩部分，其中一部分記錄的關鍵字均比另一部分記錄的關鍵字小，則可分別對這兩部分記錄繼續進行排序，以達到整個序列有序的目的。

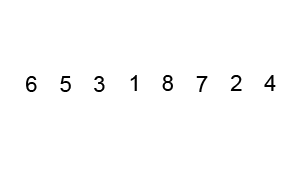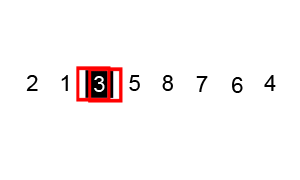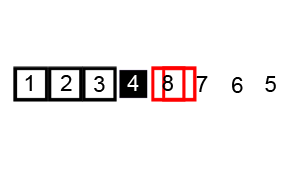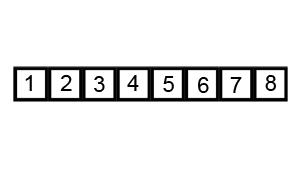
快速排序的核心步驟為：

①獲取中軸元素

②i從左至右掃描，如果小於基準元素，則i自增，否則記下a[i]

③j從右至左掃描，如果大於基準元素，則i自減，否則記下a[j]

④交換a[i]和a[j]

⑤重複這一步驟直至i和j交錯，然後和基準元素比較，然後交換。

　　（1）主入口：獲取索引並對左右兩個區間進行遞迴操作

    public static void QuickSort(T[] arr, int low, int high)
    {
        if (low < high)
        {
            int index = Partition(arr, low, high);
            // 對左區間遞迴排序
            QuickSort(arr, low, index - 1);
            // 對右區間遞迴排序
            QuickSort(arr, index + 1, high);
        }
    }

　　（2）核心：獲取基準值的實際儲存位置

    private static int Partition(T[] arr, int low, int high)
    {
        int i = low, j = high;
        T temp = arr[i]; // 確定第一個元素作為"基準值"

        while (i < j)
        {
            // Stage1:從右向左掃描直到找到比基準值小的元素
            while (i < j && arr[j].CompareTo(temp) >= 0)
            {
                j--;
            }
            // 將比基準值小的元素移動到基準值的左端
            arr[i] = arr[j];

            // Stage2:從左向右掃描直到找到比基準值大的元素
            while (i<j && arr[i].CompareTo(temp) <= 0)
            {
                i++;
            }
            // 將比基準值大的元素移動到基準值的右端
            arr[j] = arr[i];
        }

        // 記錄歸位
        arr[i] = temp;

        return i;
    }

　　在10000個隨機數的陣列中測試的效能結果如下圖所示：

　　從上圖可以看出，快速排序對於無序待排序陣列的耗時只有15ms，比Shell排序還快了6ms，它的確是“快速”的。

　　總結：快速排序的平均時間複雜度為O(nlog₂n)，在平均時間下，快速排序時目前被認為最好的內部排序方法。但是，如果待排序記錄的初始狀態有序，則快速排序則會退化為氣泡排序，其時間複雜度為O(n²)。換句話說，待排序記錄越無序，基準兩側記錄數量越接近，排序速度越快；相反，待排序記錄越有序，則排序速度越慢。

　　對於快速排序的改進一般集中在以下幾個方面：

　　①當劃分到較小的子序列時，通常可以使用插入排序替代快速排序；

　　②使用三平均分割槽法代替第一個元素作為基準值所出現的某些分割槽嚴重不均的極端情況；

　　③使用並行化處理排序；

三、選擇類排序

　　選擇排序（Selection Sort）是以選擇為基礎的一種常用排序方法，其基本思想是：每一趟從待排序的記錄中選出關鍵字最小的記錄，順序放在已排好序的記錄序列的最後，直到全部排列完為止。

3.1 簡單選擇排序

　　簡單選擇排序的基本思想是：第一趟從所有的n個記錄中選擇最小的記錄放在第一位，第二趟從n-1個記錄中選擇最小的記錄放到第二位。以此類推，經過n-1趟排序之後，整個待排序序列就成為有序序列了。

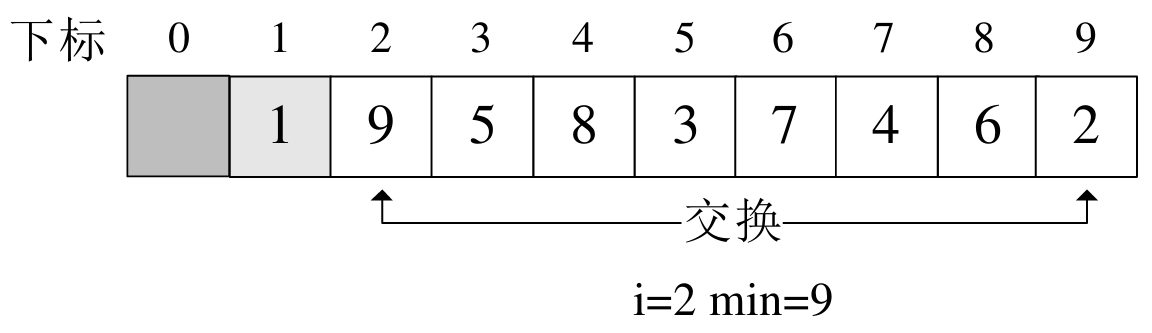
    public static void SimpleSelectSort(T[] arr)
    {
        int i, j, k;
        T temp;

        for (i = 0; i < arr.Length - 1; i++)
        {
            k = i; // k用於記錄每一趟排序中最小元素的索引號
            for (j = i + 1; j < arr.Length; j++)
            {
                if (arr[j].CompareTo(arr[k]) < 0)
                {
                    k = j;
                }
            }

            if(k != i)
            {
                // 交換arr[k]和arr[i]
                temp = arr[k];
                arr[k] = arr[i];
                arr[i] = temp;
            }
        }
    }

　　在10000個隨機數的陣列中測試的效能結果如下圖所示：

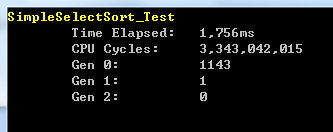
　　總結：簡單選擇排序外迴圈n-1趟，內迴圈執行n-i趟，因此，簡單選擇排序的平均時間複雜度為O(n²)，和直接插入排序、氣泡排序一樣均超過了1秒鐘。

3.2 堆排序

　　堆排序（Heap Sort）是由J.Williams在1964年提出的，它是在選擇排序的基礎上發展起來的，比選擇排序的效率要高，因此也可以說堆排序是選擇排序的升級版。堆排序除了是一種排序方法外，還涉及到方法之外的一些概念：堆和完全二叉樹。這裡主要說說什麼是堆？

　　如果將堆看成一棵完全二叉樹，則這棵完全二叉樹中的每個非葉子節點的值均不大於（或不小於）其左、右孩子節點的值。由此可知，若一棵完全二叉樹是堆，則根節點一定是這棵樹的所有節點的最小元素或最大元素。非葉子節點的值大於其左、右孩子節點的值的堆稱為大根堆，反之則稱為下小根堆，如下圖所示。

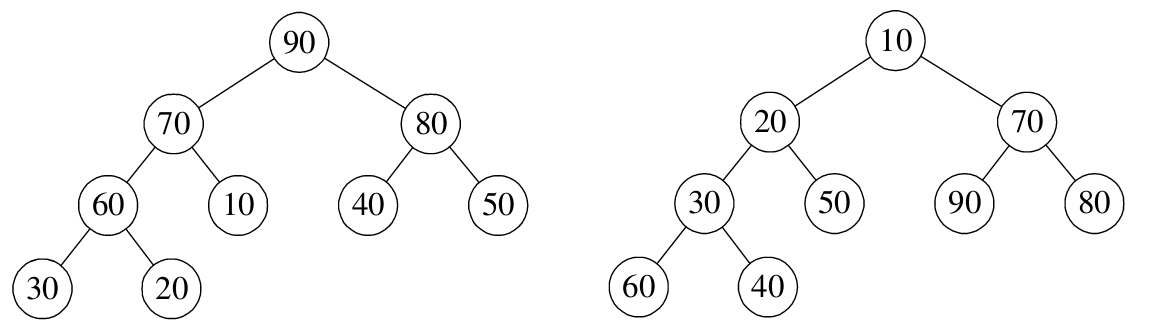
　　如果按照層序遍歷的方式給結點從1開始編號，則結點之間滿足如下關係：

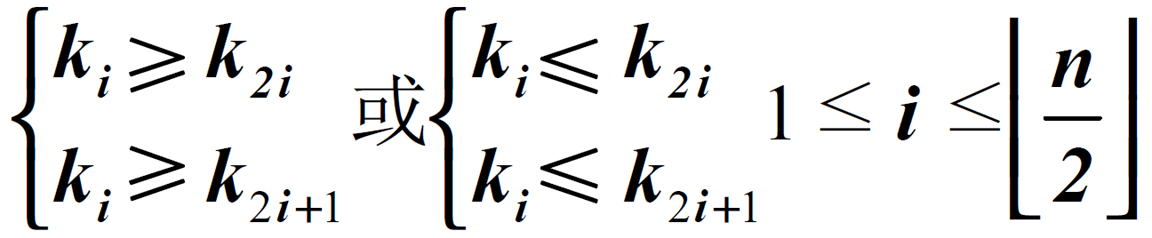
　　（1）基本思想

　　堆排序的基本思想是：首先將待排序的記錄序列構造為一個堆，此時選擇堆中所有記錄的最小記錄或最大記錄，然後將它從堆中移出，並將剩餘的記錄再調整成堆，這樣就又找到了次大（或次小）的記錄。以此類推，直到堆中只有一個記錄為止，每個記錄出堆的順序就是一個有序序列。

　　（2）處理步驟

　　堆排序的處理步驟如下：

①設堆中元素個數為n，先取i=n/2-1，將以i節點為根的子樹調整成堆，然後令i=i-1。再將以i節點為根的子樹調整成堆，如此反覆，直到i=0為止，即完成初始堆的建立過程；

②首先輸出堆頂元素，將堆中最後一個元素上移到原堆頂位置，這樣可能會破壞原有堆的特性，這時需要重複步驟①的操作來恢復堆；

③重複執行步驟②，直到輸出全部元素為止。按輸出元素的前後次序排列起來，就是一個有序序列，從而也就完成了對排序操作。

　　假設待排序序列為（3,6,5,9,7,1,8,2,4），那麼根據此序列建立大根堆的過程如下：

　　①將（3,6,5,9,7,1,8,2,4）按照二叉樹的順序儲存結構轉換為如下圖所示的完全二叉樹；

　　②首先，因為n=9，所以i=n/2-1=3，即調整以節點9為根的子樹，由於節點9均大於它的孩子節點2和4，所以不需要交換；最後，i=i-1=2。

　　③當i=2時，即調整以節點5為根的子樹，由於節點5小於它的右孩子8，所以5需要與8交換；最後，i=i-1=1。

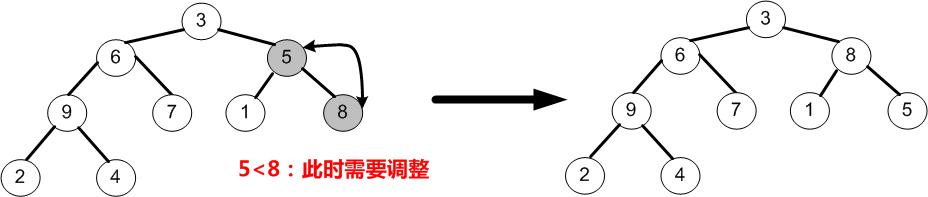
　　④當i=1時，即調整以節點6為根的子樹，由於節點6均小於它的左、右孩子9和7，故節點6需要與較大的左孩子9交換；最後i=i-1=0。

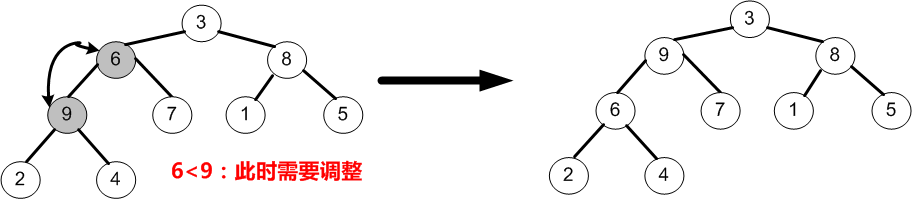
　　⑤當i=0時，即調整以3為根的子樹，由於節點3均小於它的左、右孩子9和8，故節點3需要與較大的左孩子9交換；交換之後又因為節點3小於它的左、右孩子節點6和7，於是需要與較大的右孩子7交換。

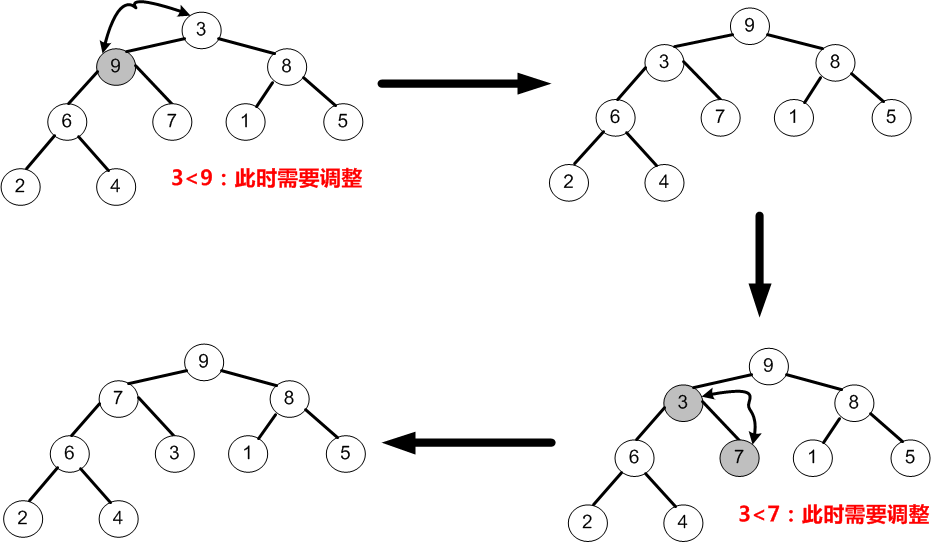
　　⑥如上圖所示，至此就完成了初始堆的建立，待排序序列變為（9,7,8,6,3,1,5,2,4）。

　　（3）程式碼實現

　　①主入口：首先遞迴建立初始堆，其次遞迴調整大根堆；

    public static void HeapSort(T[] arr)
    {
        int n = arr.Length; // 獲取序列的長度
        // 構造初始堆
        for (int i = n / 2 - 1; i >= 0; i--)
        {
            Sift(arr, i, n - 1);
        }
        // 進行堆排序
        T temp;
        for (int i = n - 1; i >= 1; i--)
        {
            temp = arr[0];       // 獲取堆頂元素
            arr[0] = arr[i];     // 將堆中最後一個元素移動到堆頂
            arr[i] = temp;       // 最大元素歸位,下一次不會再參與計算

            Sift(arr, 0, i - 1); // 重新遞迴調整堆
        }
    }

　　②核心：建立堆的過程；

    private static void Sift(T[] arr, int low, int high)
    {
        // i為欲調整子樹的根節點索引號，j為這個節點的左孩子
        int i = low, j = 2 * i + 1;
        // temp記錄根節點的值
        T temp = arr[i];

        while (j <= high)
        {
            // 如果左孩子小於右孩子，則將要交換的孩子節點指向右孩子
            if (j < high && arr[j].CompareTo(arr[j + 1]) < 0)
            {
                j++;
            }
            // 如果根節點小於它的孩子節點
            if (temp.CompareTo(arr[j]) < 0)
            {
                arr[i] = arr[j]; // 交換根節點與其孩子節點
                i = j;  // 以交換後的孩子節點作為根節點繼續調整其子樹
                j = 2 * i + 1;  // j指向交換後的孩子節點的左孩子
            }
            else
            {
                // 調整完畢，可以直接退出
                break;
            }
        }
        // 使最初被調整的節點存入正確的位置
        arr[i] = temp;
    }

　　在10000個隨機數的陣列中測試的效能結果如下圖所示：

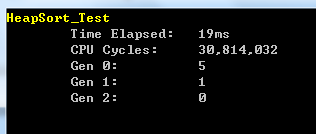
　　從上圖可以看出，快速排序對於無序待排序陣列的耗時只有19ms，比Shell排序還快了2ms，僅僅比快速排序慢了4ms，可以說跟快速排序一樣快。

　　總結：堆排序的執行時間主要由建立初始堆和反覆調整堆這兩個部分的時間開銷組成，由於堆排序對原始記錄的排序狀態並不敏感，因此它無論是最好、最壞和平均時間複雜度均為O(nlog₂n)。這在效能上顯然要遠遠好過於冒泡、簡單選擇、直接插入的O(n²)的時間複雜度了。另外，由於初始構建堆所需的比較次數較多，因此，它並不適合待排序序列個數較少的情況。

四、歸併類排序

　　歸併排序（Merging Sort）是利用“歸併”技術進行的排序，所謂歸併是指將兩個或兩個以上的有序表合併成一個新的有序表。其基本思想是：將這些有序的子序列進行合併，從而得到有序的序列。

4.1 二路歸併排序介紹

　　利用兩個有序序列的合併實現歸併排序就稱為二路歸併排序，其基本思想是：如果初始序列含有n個記錄，則可以看成是n個有序的子序列，每個子序列的長度為1，然後兩兩歸併，得到（表示不小於x的最小整數）個長度為2或1的有序子序列；再兩兩歸併，……，如此重複，直至得到一個長度為n的有序序列為止。

　　例如一個本是無序的陣列序列{16,7,13,10,9,15,3,2,5,8,12,1,11,4,6,14}，通過兩兩合併排序後再合併，最終獲得了一個有序的陣列，如下圖所示：

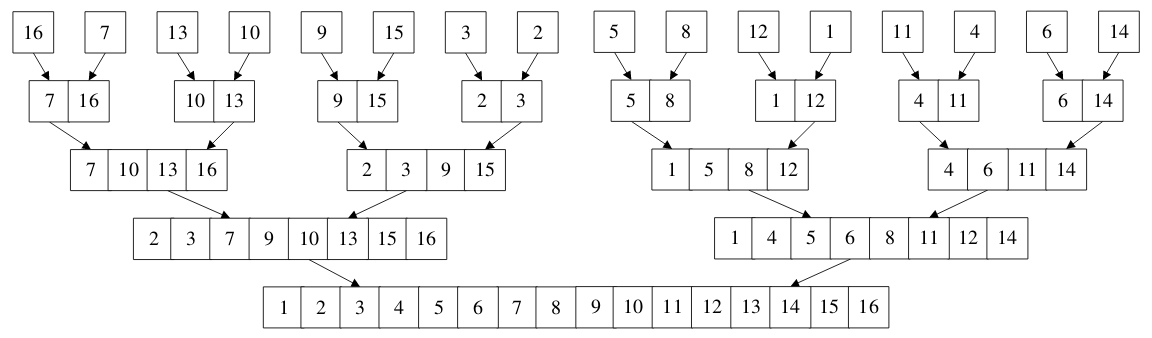
　　觀察上圖，細心的你會驚訝，它十分像一棵倒置的完全二叉樹，通常涉及到完全二叉樹結構的排序演算法，效率一般都不會低。

4.2 二路歸併排序實現

　　（1）主入口：首先歸併左邊子序列，其次歸併右邊子序列，最後歸併當前序列

    public static void MergeSort(T[] arr, int low, int high)
    {
        if (low < high)
        {
            int mid = (low + high) / 2;
            MergeSort(arr, low, mid);       // 歸併左邊的子序列（遞迴）
            MergeSort(arr, mid + 1, high);  // 歸併右邊的子序列（遞迴）
            Merge(arr, low, mid, high);     // 歸併當前前序列
        }
    }

　　（2）核心：將兩個有序的子序列合併成一個有序序列

    private static void Merge(T[] arr, int low, int mid, int high)
    {
        // result為臨時空間，用於存放合併後的序列
        T[] result = new T[high - low + 1];
        int i = low, j = mid + 1, k = 0;
        // 合併兩個子序列
        while (i <= mid && j <= high)
        {
            if (arr[i].CompareTo(arr[j]) < 0)
            {
                result[k++] = arr[i++];
            }
            else
            {
                result[k++] = arr[j++];
            }
        }
        // 將左邊子序列的剩餘部分複製到合併後的序列
        while (i <= mid)
        {
            result[k++] = arr[i++];
        }
        // 將右邊子序列的剩餘部分複製到合併後的序列
        while (j <= high)
        {
            result[k++] = arr[j++];
        }
        // 將合併後的序列覆蓋合併前的序列
        for (k = 0, i = low; i <= high; k++, i++)
        {
            arr[i] = result[k];
        }
    }

　　在10000個隨機數的陣列中測試的效能結果如下圖所示：

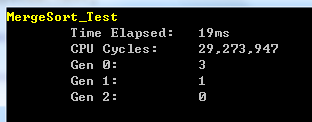
　　從上圖可以看出，快速排序對於無序待排序陣列的耗時也只有19ms，跟快速排序、堆排序屬於一個級別。

　　總結：二路歸併排序易於在連結串列上實現，它的時間複雜度在最好、最壞情況下均為O(nlog₂n)，但二路歸併排序與其他排序相比，需要更多的臨時空間。從Merge方法可以看出，需要頻繁地建立臨時空間來儲存合併後的資料，可以讓所有的Merge方法共用同一塊臨時空間，以最大限度地減少記憶體使用。

五、小結

　　本篇複習了多種排序方法，但其中並無絕對好與不好的演算法，每一種排序方法都有其優缺點，適合於不同的環境。因此，在實際應用中，應根據具體情況作出選擇。

　　（1）當待排序序列的記錄數n較小的時候（一般n<=50），可以採用直接插入排序、直接選擇排序或氣泡排序：

　　若序列初始狀態基本為正序，則應選用直接插入排序、氣泡排序。

　　如果單條記錄本身資訊量較大，由於直接插入排序所需的記錄移動操作較直接選擇排序多，因此用直接選擇排序較好。

　　（2）當待排序序列的記錄數n較大的時候，則應採用時間複雜度為O(nlog₂n)的排序方法，如：快速排序、堆排序或歸併排序。

　　快速排序時目前基於比較的內部排序中被認為是最好的方法，當待排序的關鍵字隨機分佈時，快速排序的平均時間最短，.NET中集合類的內建排序方法（例如：Array.Sort()）也是使用了快速排序實現的。

　　堆排序需要的輔助空間少於快速排序，並且不會出現快速排序可能出現的最壞情況O(n²)。

　　歸併排序需要大量的輔助空間，因此不值得提倡使用，但是如果要將兩個有序序列組合成一個新的有序序列，最好的方法就是歸併排序。

參考資料

（1）陳廣，《資料結構（C#語言描述）》

（2）程傑，《大話資料結構》

（3）段恩澤，《資料結構（C#語言版）》

作者：周旭龍

本文版權歸作者和部落格園共有，歡迎轉載，但未經作者同意必須保留此段宣告，且在文章頁面明顯位置給出原文連結。