前面幾篇已經介紹了線性表和樹兩類資料結構，線性表中的元素是“一對一”的關係，樹中的元素是“一對多”的關係，本章所述的圖結構中的元素則是“多對多”的關係。圖（Graph）是一種複雜的非線性結構，在圖結構中，每個元素都可以有零個或多個前驅，也可以有零個或多個後繼，也就是說，元素之間的關係是任意的。現實生活中的很多事物都可以抽象為圖，例如世界各地接入Internet的計算機通過網線連線在一起，各個城市和城市之間的鐵軌等等。

一、圖的基本概念

1.1 多對多的複雜關係

　　現實中人與人之間關係非常複雜，比如我認識的朋友，可能他們之間也互相認識，這不是簡單的一對一、一對多，研究人際關係很自然會考慮多對多的情況。圖是一種較線性表和樹更加複雜的資料結構。在圖形結構中，結點之間的關係可以是任意的，圖中任意兩個資料元素之間都可能相關。

定義：圖（Graph）是由頂點的有窮非空集合和頂點之間邊的集合組成，通常表示為：G(V,E)，其中，G表示一個圖，V是圖G中頂點的集合，E是圖G中邊的集合。

　　在圖中需要注意的是：

　　（1）線性表中我們把資料元素叫元素，樹中將資料元素叫結點，在圖中資料元素，我們則稱之為頂點（Vertex）。

　　（2）線性表可以沒有元素，稱為空表；樹中可以沒有節點，稱為空樹；但是，在圖中不允許沒有頂點（有窮非空性）。

　　（3）線性表中的各元素是線性關係，樹中的各元素是層次關係，而圖中各頂點的關係是用邊來表示（邊集可以為空）。

1.2 紛繁冗多的術語

　　圖的基本術語有很多，本文只挑選幾個特別重要的來說明，其餘的請閱讀相關教材。

　　（1）無向圖

　　如果圖中任意兩個頂點之間的邊都是無向邊（簡而言之就是沒有方向的邊），則稱該圖為無向圖（Undirected graphs）。

　　（2）有向圖

　　如果圖中任意兩個頂點之間的邊都是有向邊（簡而言之就是有方向的邊），則稱該圖為有向圖（Directed graphs）。

　　（3）完全圖

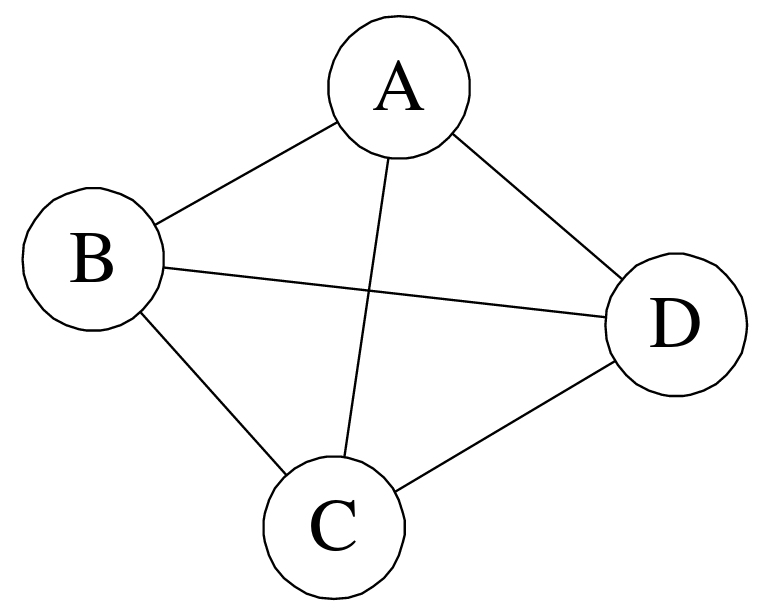
　　①無向完全圖：在無向圖中，如果任意兩個頂點之間都存在邊，則稱該圖為無向完全圖。（含有n個頂點的無向完全圖有(n×(n-1))/2條邊）如下圖所示：

　　②有向完全圖：在有向圖中，如果任意兩個頂點之間都存在方向互為相反的兩條弧，則稱該圖為有向完全圖。（含有n個頂點的有向完全圖有n×(n-1)條邊）如下圖所示：

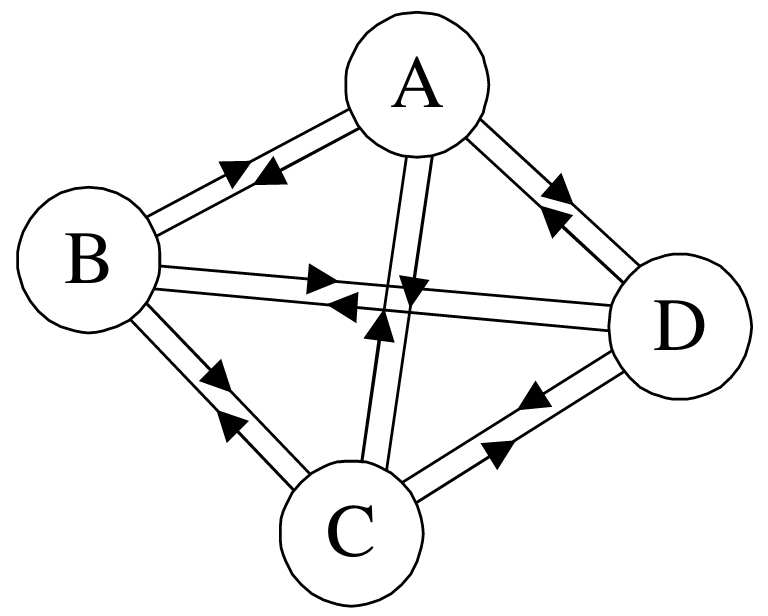
PS：當一個圖接近完全圖時，則稱它為稠密圖（Dense Graph），而當一個圖含有較少的邊時，則稱它為稀疏圖（Spare Graph）。

　　（4）頂點的度

　　頂點Vi的度（Degree）是指在圖中與Vi相關聯的邊的條數。對於有向圖來說，有入度（In-degree）和出度（Out-degree）之分，有向圖頂點的度等於該頂點的入度和出度之和。

　　（5）鄰接

　　①若無向圖中的兩個頂點V1和V2存在一條邊(V1,V2)，則稱頂點V1和V2鄰接（Adjacent）；

　　②若有向圖中存在一條邊<V3,V2>，則稱頂點V3與頂點V2鄰接，且是V3鄰接到V2或V2鄰接直V3；

PS：無向圖中的邊使用小括號“()”表示，而有向圖中的邊使用尖括號“<>”表示。

　　（6）路徑

　　在無向圖中，若從頂點Vi出發有一組邊可到達頂點Vj，則稱頂點Vi到頂點Vj的頂點序列為從頂點Vi到頂點Vj的路徑（Path）。

　　（7）連通

　　若從Vi到Vj有路徑可通，則稱頂點Vi和頂點Vj是連通（Connected）的。

　　（8）權

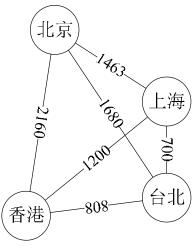
　　有些圖的邊或弧具有與它相關的數字，這種與圖的邊或弧相關的數叫做權（Weight）。

二、圖的儲存結構

圖的儲存結構除了要儲存圖中的各個頂點本身的資訊之外，還要儲存頂點與頂點之間的關係，因此，圖的結構也比較複雜。常用的圖的儲存結構有鄰接矩陣和鄰接表等。

2.1 鄰接矩陣表示法

　　圖的鄰接矩陣（Adjacency Matrix）儲存方式是用兩個陣列來表示圖。一個一維陣列儲存圖中頂點資訊，一個二維陣列（稱為鄰接矩陣）儲存圖中的邊或弧的資訊。

　　（1）無向圖：

　　我們可以設定兩個陣列，頂點陣列為vertex[4]={v0,v1,v2,v3}，邊陣列arc[4][4]為上圖右邊這樣的一個矩陣。對於矩陣的主對角線的值，即arc[0][0]、arc[1][1]、arc[2][2]、arc[3][3]，全為0是因為不存在頂點的邊。

　　（2）有向圖：

　　我們再來看一個有向圖樣例，如下圖所示的左邊。頂點陣列為vertex[4]={v0,v1,v2,v3}，弧陣列arc[4][4]為下圖右邊這樣的一個矩陣。主對角線上數值依然為0。但因為是有向圖，所以此矩陣並不對稱，比如由v1到v0有弧，得到arc[1][0]=1，而v到v沒有弧，因此arc[0][1]=0。

不足：由於存在n個頂點的圖需要n*n個數組元素進行儲存，當圖為稀疏圖時，使用鄰接矩陣儲存方法將會出現大量0元素，這會造成極大的空間浪費。這時，可以考慮使用鄰接表表示法來儲存圖中的資料。

2.2 鄰接表表示法

　　首先，回憶我們線上性表時談到，順序儲存結構就存在預先分配記憶體可能造成儲存空間浪費的問題，於是引出了鏈式儲存的結構。同樣的，我們也可以考慮對邊或弧使用鏈式儲存的方式來避免空間浪費的問題。

　　鄰接表由表頭節點和表節點兩部分組成，圖中每個頂點均對應一個儲存在陣列中的表頭節點。如果這個表頭節點所對應的頂點存在鄰接節點，則把鄰接節點依次存放於表頭節點所指向的單向連結串列中。

　　（1）無向圖：下圖所示的就是一個無向圖的鄰接表結構。

　　從上圖中我們知道，頂點表的各個結點由data和firstedge兩個域表示，data是資料域，儲存頂點的資訊，firstedge是指標域，指向邊表的第一個結點，即此頂點的第一個鄰接點。邊表結點由adjvex和next兩個域組成。adjvex是鄰接點域，儲存某頂點的鄰接點在頂點表中的下標，next則儲存指向邊表中下一個結點的指標。例如：v1頂點與v0、v2互為鄰接點，則在v1的邊表中，adjvex分別為v0的0和v2的2。

PS：對於無向圖來說，使用鄰接表進行儲存也會出現資料冗餘的現象。例如上圖中，頂點V0所指向的連結串列中存在一個指向頂點V3的同事，頂點V3所指向的連結串列中也會存在一個指向V0的頂點。

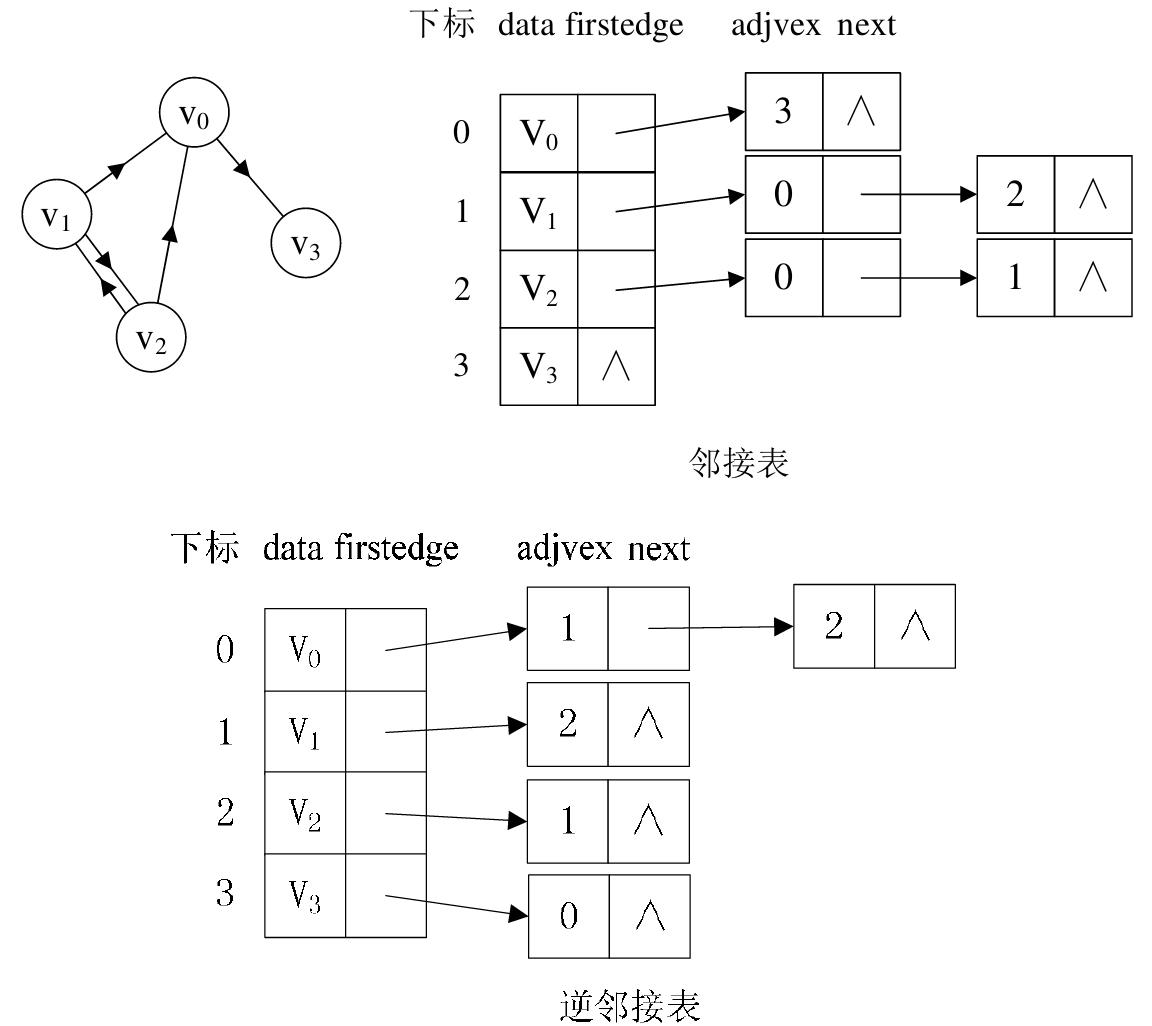
　　（2）有向圖：若是有向圖，鄰接表結構是類似的，但要注意的是有向圖由於有方向的。因此，有向圖的鄰接表分為出邊表和入邊表（又稱逆鄰接表），出邊表的表節點存放的是從表頭節點出發的有向邊所指的尾節點；入邊表的表節點存放的則是指向表頭節點的某個頂點，如下圖所示。

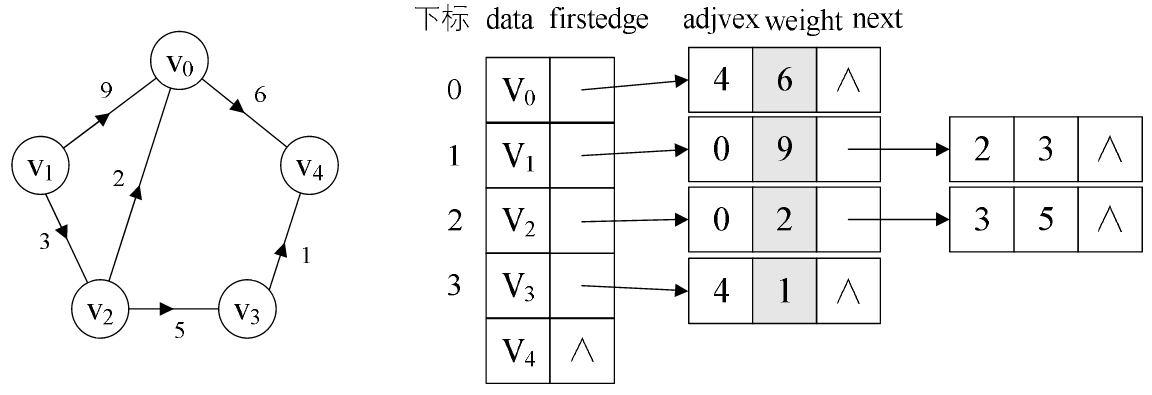
　　（3）帶權圖：對於帶權值的網圖，可以在邊表結點定義中再增加一個weight的資料域，儲存權值資訊即可，如下圖所示。

三、圖的模擬實現

PS：由於鄰接矩陣容易造成空間資源的浪費，因此這裡只考慮使用鄰接表來實現。

3.1 總體設計結構

　　（1）連結串列節點定義

　　①表頭節點Vertex

        /// <summary>
        /// 巢狀類：存放於陣列中的表頭節點
        /// </summary>
        /// <typeparam name="TValue"></typeparam>
        protected class Vertex<TValue>
        {
            public TValue data;     // 資料
            public Node firstEdge;  // 鄰接點連結串列頭指標
            public bool isVisited;  // 訪問標誌：遍歷時使用

            public Vertex()
            {
                this.data = default(TValue);
            }

            public Vertex(TValue value)
            {
                this.data = value;
            }
        }

　　②表節點Node

        /// <summary>
        /// 巢狀類：連結串列中的表節點
        /// </summary>
        protected class Node
        {
            public Vertex<T> adjvex;    // 鄰接點域
            public Node next;           // 下一個鄰接點指標域

            public Node()
            {
                this.adjvex = null;
            }

            public Node(Vertex<T> value)
            {
                this.adjvex = value;
            }
        }

　　（2）鄰接表總體定義

    public class MyAdjacencyList<T> where T : class
    {
        private List<Vertex<T>> items;  // 圖的頂點集合

        public MyAdjacencyList()
            : this(10)
        {
        }

        public MyAdjacencyList(int capacity)
        {
            this.items = new List<Vertex<T>>(capacity);
        }
    
        #region 基本方法：為圖中新增頂點、新增有向與無向邊
        #endregion
    
        #region 輔助方法：圖中是否包含某個元素、查詢指定頂點、初始化visited標誌
        #endregion
        
        #region 巢狀類：表頭節點與表節點定義
        #endregion
    }

　　首先，我們使用了一個動態集合List來代替陣列儲存Vertex的集合，預設容量為10，且不需要陣列儲存空間不夠的情況，簡化了操作。其次，我們要定義一些基本方法，如新增頂點、新增邊。還要定義一些輔助方法，如判斷是否包含某個元素等（詳見完整程式碼檔案）。最後，我們再實現圖的一些遍歷演算法，如深度優先遍歷與廣度優先遍歷（本篇不作介紹，下一篇再介紹）。

3.2 基本方法實現

　　（1）新增一個頂點

        /// <summary>
        /// 新增一個頂點
        /// </summary>
        /// <param name="item">頂點元素data</param>
        public void AddVertex(T item)
        {
            if (Contains(item))
            {
                throw new ArgumentException("添加了重複的頂點！");
            }

            Vertex<T> newVertex = new Vertex<T>(item);
            items.Add(newVertex);
        }

　　就是往集合裡邊加入新元素；

　　（2）新增一條邊

　　這裡需要分為兩種情況，一種是新增無向圖的邊，這時無向圖的兩個頂點都需要記錄邊的資訊。另一種則是新增有向圖的邊，這時只需要一條記錄；

　　①無向圖

        /// <summary>
        /// 新增一條無向邊
        /// </summary>
        /// <param name="from">頭頂點data</param>
        /// <param name="to">尾頂點data</param>
        /// <param name="weight">權值</param>
        public void AddEdge(T from, T to)
        {
            Vertex<T> fromVertex = Find(from);
            if (fromVertex == null)
            {
                throw new ArgumentException("頭頂點不存在！");
            }

            Vertex<T> toVertex = Find(to);
            if (toVertex == null)
            {
                throw new ArgumentException("尾頂點不存在！");
            }

            // 無向圖的兩個頂點都需要記錄邊的資訊
            AddDirectedEdge(fromVertex, toVertex);
            AddDirectedEdge(toVertex, fromVertex);
        }

　　這裡可以看到這兩句程式碼，對應的兩個頂點都記錄了邊的資訊。

    // 無向圖的兩個頂點都需要記錄邊的資訊
    AddDirectedEdge(fromVertex, toVertex);
    AddDirectedEdge(toVertex, fromVertex);

　　②有向圖

        /// <summary>
        /// 新增一條有向邊
        /// </summary>
        /// <param name="from">頭結點data</param>
        /// <param name="to">尾節點data</param>
        public void AddDirectedEdge(T from, T to)
        {
            Vertex<T> fromVertex = Find(from);
            if (fromVertex == null)
            {
                throw new ArgumentException("頭頂點不存在！");
            }

            Vertex<T> toVertex = Find(to);
            if (toVertex == null)
            {
                throw new ArgumentException("尾頂點不存在！");
            }

            AddDirectedEdge(fromVertex, toVertex);
        }

　　③如何新增邊

　　在實現中，無論是無線圖還是有向圖都是新增的有向邊，只不過無向圖是添加了兩條有向邊：

        /// <summary>
        /// 新增一條有向邊
        /// </summary>
        /// <param name="fromVertex">頭頂點</param>
        /// <param name="toVertex">尾頂點</param>
        private void AddDirectedEdge(Vertex<T> fromVertex, Vertex<T> toVertex)
        {
            if (fromVertex.firstEdge == null)
            {
                fromVertex.firstEdge = new Node(toVertex);
            }
            else
            {
                Node temp = null;
                Node node = fromVertex.firstEdge;

                do
                {
                    // 檢查是否添加了重複邊
                    if (node.adjvex.data.Equals(toVertex.data))
                    {
                        throw new ArgumentException("添加了重複的邊！");
                    }
                    temp = node;
                    node = node.next;
                } while (node != null);

                Node newNode = new Node(toVertex);
                temp.next = newNode;
            }
        }

　　（3）列印每個頂點及其鄰接點的資訊

        /// <summary>
        /// 列印列印每個頂點和它的鄰接點
        /// </summary>
        /// <param name="isDirectedGraph">是否是有向圖</param>
        public string GetGraphInfo(bool isDirectedGraph = false)
        {
            StringBuilder sb = new StringBuilder();
            foreach (Vertex<T> v in items)
            {
                sb.Append(v.data.ToString() + ":");
                if (v.firstEdge != null)
                {
                    Node temp = v.firstEdge;
                    while (temp != null)
                    {
                        if (isDirectedGraph)
                        {
                            sb.Append(v.data.ToString() + "→" + temp.adjvex.data.ToString() + " ");
                        }
                        else
                        {
                            sb.Append(temp.adjvex.data.ToString());
                        }
                        temp = temp.next;
                    }
                }
                sb.Append("\r\n");
            }

            return sb.ToString();
        }

　　這裡判斷了是否是有向圖，如果是有向圖則顯示A→B的形式，如果是無向圖則顯示A：B的形式。

3.3 基本功能測試

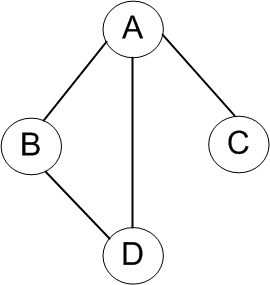
　　這裡我們對基本功能做一下測試，分為無向圖和有向圖，首先插入頂點及對應邊，然後列印頂點及其鄰接表的資訊，要構造的無向圖與有向圖如上面兩張圖所示，測試程式碼如下所示：

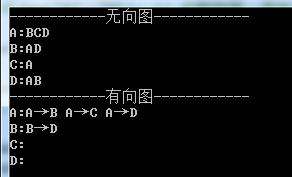
        static void MyAdjacencyListTest()
        {
            Console.WriteLine("------------無向圖------------");
            MyAdjacencyList<string> adjList = new MyAdjacencyList<string>();
            // 新增頂點
            adjList.AddVertex("A");
            adjList.AddVertex("B");
            adjList.AddVertex("C");
            adjList.AddVertex("D");
            //adjList.AddVertex("D"); // 會報異常：添加了重複的節點
            // 新增無向邊
            adjList.AddEdge("A", "B");
            adjList.AddEdge("A", "C");
            adjList.AddEdge("A", "D");
            adjList.AddEdge("B", "D");
            //adjList.AddEdge("B", "D"); // 會報異常：添加了重複的邊

            Console.Write(adjList.GetGraphInfo());

            Console.WriteLine("------------有向圖------------");
            MyAdjacencyList<string> dirAdjList = new MyAdjacencyList<string>();
            // 新增頂點
            dirAdjList.AddVertex("A");
            dirAdjList.AddVertex("B");
            dirAdjList.AddVertex("C");
            dirAdjList.AddVertex("D");
            // 新增有向邊
            dirAdjList.AddDirectedEdge("A", "B");
            dirAdjList.AddDirectedEdge("A", "C");
            dirAdjList.AddDirectedEdge("A", "D");
            dirAdjList.AddDirectedEdge("B", "D");

            Console.Write(dirAdjList.GetGraphInfo(true));
        }

　　執行結果如下圖所示：

附件下載

參考資料

（1）程傑，《大話資料結構》

（2）陳廣，《資料結構（C#語言描述）》

（3）段恩澤，《資料結構（C#語言版）》

作者：周旭龍

本文版權歸作者和部落格園共有，歡迎轉載，但未經作者同意必須保留此段宣告，且在文章頁面明顯位置給出原文連結。