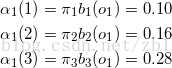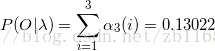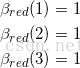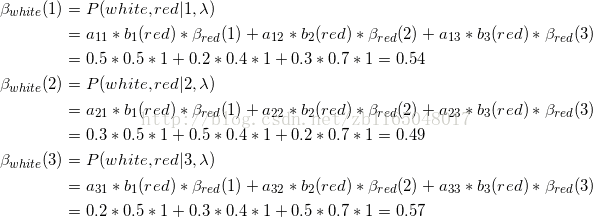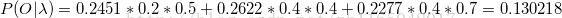前向-後向演算法例項
已知HMM模型引數:
轉移概率矩陣A:
| 0.5 | 0.2 | 0.3 |
| 0.3 | 0.5 | 0.2 |
| 0.2 | 0.3 | 0.5 |
| 0.5 | 0.5 |
| 0.4 | 0.6 |
| 0.7 | 0.3 |
π=(0.2 , 0.4 , 0.4)
求解:三次取球顏色為(紅、白、紅)的概率P(O|λ)
提示:盒子相當於三種隱狀態,兩種顏色的球相當於觀測情況,觀測序列由(紅、白、紅)給出
(1)計算初值
a1(2) 代表第一個時間下, 從第二個盒子裡取出紅球的概率
(2)遞推計算
(3)終止條件
關於後向演算法,直接以盒子(隱)和球(觀測)的例項為例推導:
(1)初始化第三次取球為紅球時候,即最終時刻所有狀態的概率為1
式中下標為觀測情況,括號為隱狀態,比如第一個式子意思就是第一個隱狀態對應的觀測到紅球的概率
(2)逆推迭代倒數第二次觀察情況為白球的情況
第一個式子表示的是第二次觀測,如果狀態為1,那麼第二、三次觀測為(白、紅)的聯合概率分佈,a是第二層隱狀態(第一個盒子)轉移到第三層隱狀態(三個盒子)的轉移概率,b表示第三層的三個隱狀態觀測到紅球的概率,β(等式右邊)表示已知模型引數和第三層隱狀態,求第三次觀測到紅球的概率,其實第(1)步計算是1
第二個式子表示的是第二次觀測,如果狀態為2,那麼第二、三次觀測為(白、紅)的聯合概率分佈,a是第二層隱狀態(第二個盒子)轉移到第三層隱狀態(三個盒子)的轉移概率,b表示第三層的三個隱狀態觀測到紅球的概率,β(等式右邊)表示已知模型引數和第三層隱狀態,求第三次觀測到紅球的概率,其實第(1)步計算是1
同理推導第一層的情況
(3)計算加和
可以發現前向演算法和後向演算法的結果相同
【注】前向演算法中計算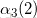
相關推薦
前向-後向演算法例項
已知HMM模型引數:轉移概率矩陣A:0.50.20.30.30.50.20.20.30.5混淆矩陣B:0.50.50.40.60.70.3初始概率:π=(0.2 , 0.4 , 0.4)求解:三次取球顏色為(紅、白、紅)的概率P(O|λ)提示:盒子相當於三種隱狀態,兩種顏色的
隱馬爾科夫模型(前向後向演算法、鮑姆-韋爾奇演算法、維特比演算法)
概率圖模型是一類用圖來表達變數相關關係的概率模型。它以圖為表示工具,最常見的是用一個結點表示一個或一組隨機變數,結點之間的變表是變數間的概率相關關係。根據邊的性質不同,可以將概率圖模型分為兩類:一類是使用有向無環圖表示變數間的依賴關係,稱為有向圖模型或貝葉斯網;另一類是使用無向圖表示變數間的相關關係,稱為無
HMM前向演算法,維位元演算法,後向演算法,前向後向演算法程式碼
typedef struct { int N; /* 隱藏狀態數目;Q={1,2,…,N} */ int M; /* 觀察符號數目; V={1,2,…,M}*/ double **A; /* 狀態轉移矩陣A[1..N][1..N]. a[i][j] 是從t時刻狀態i到t+1
隱馬爾科夫模型(HMMs)之五:維特比演算法及前向後向演算法
維特比演算法(Viterbi Algorithm) 找到可能性最大的隱藏序列 通常我們都有一個特定的HMM,然後根據一個可觀察序列去找到最可能生成這個可觀察序列的隱藏序列。 1.窮舉搜尋 我們可以在下圖中看到每個狀態和觀察的關係。 通過計算所有可能的隱藏序列的概率,
機器學習筆記(十四)——HMM估計問題和前向後向演算法
一、隱馬爾科夫鏈的第一個基本問題 估計問題:給定一個觀察序列O=O1O2…OT和模型u=(A,B,π),如何快速地計算出給定模型u情況下,觀察序列O的概率, 即P(O|u)? 二、求解觀察序列的概率 其實,求解這個問題就是一個解碼問題。
HMM-前向後向演算法
### 基本要素 - 狀態 $N$個 - 狀態序列 $S = s_1,s_2,...$ - 觀測序列 $O=O_1,O_2,...$ - $\lambda(A,B,\pi)$ - 狀態轉移概率 $A = \{a_{ij}\}$ - 發射概率 $B = \{b_{ik}\}$ - 初
HMM-前向後向演算法理解與實現(python)
[TOC] ### 基本要素 - 狀態 $N$個 - 狀態序列 $S = s_1,s_2,...$ - 觀測序列 $O=O_1,O_2,...$ - $\lambda(A,B,\pi)$ - 狀態轉移概率 $A = \{a_{ij}\}$ - 發射概率 $B = \{b_{ik}\}$
隱馬爾科夫模型HMM(二)前向後向算法評估觀察序列概率
流程 來看 遞推 limits its 可能 基本 通過 如何 隱馬爾科夫模型HMM(一)HMM模型 隱馬爾科夫模型HMM(二)前向後向算法評估觀察序列概率 隱馬爾科夫模型HMM(三)鮑姆-韋爾奇算法求解HMM參數(TODO) 隱馬爾科夫模型
HMM學習2之前向-後向演算法(轉)
void BaumWelch(HMM *phmm, int T, int *O, double **alpha, double **beta, double **gamma, int *pniter, double *plogprobinit, double *plogprobfinal) { int
多層前饋神經網路的後向傳播演算法推導
神經網路模型定義 本文研究的多層前饋神經網路(Multi-layer Feedforward Neural Networks),包含多層神經元,每層神經元與下一層神經元完全連線,神經元之間不存在同層連線,也不存在跨層連線. 設神經網路的層數為 N, 其中包括
神經網路中的前向和後向演算法
最近深度學習的研究在學界火的一塌糊塗,大老闆終於也下定決心組織實驗室開展相關研究了,何況實驗室的主流方向是做成像的,不做點這方面的研究感覺說不過去。研究生小朋友們剛進來還得看視覺方面的東西,博三博四的師兄師姐們基本都達到畢業要求了已經無心學習,最後這種為實驗
UPC-9519 New Game 前向星+Dijkstra演算法
題目傳送門 AC程式碼:(其實我也看不懂= =) #include<bits/stdc++.h> #define inf 0x3f3f3f3f using namespace std; const int maxn=1e6+7; struct Edge{ int ne
卷積神經網路CNN的前向和後向傳播(一)
卷積神經網路CNN的前向和後向傳播 卷積運算與相關的區別 卷積運算的正向和反向傳播 原文 Forward And Backpropagation in Convolutional Neural Network地址: https://medium.
卷積神經網路CNN的前向和後向傳播(二)
卷積神經網路CNN的前向和後向傳播(二) padding=1,stride=1的情形 輸入為8x8和卷積核3x3 對輸入的求導 對卷積核的求導 本文在卷積神經網路CNN的前向和後向傳播(一)的基礎上做一些擴充套件
迴圈神經網路(RNN)模型與前向反向傳播演算法
在前面我們講到了DNN,以及DNN的特例CNN的模型和前向反向傳播演算法,這些演算法都是前向反饋的,模型的輸出和模型本身沒有關聯關係。今天我們就討論另一類輸出和模型間有反饋的神經網路:迴圈神經網路(Recurrent Neural Networks ,以下簡稱RNN),它廣泛的用於自然語言處理中的語音
LSTM模型與前向反向傳播演算法
在迴圈神經網路(RNN)模型與前向反向傳播演算法中,我們總結了對RNN模型做了總結。由於RNN也有梯度消失的問題,因此很難處理長序列的資料,大牛們對RNN做了改進,得到了RNN的特例LSTM(Long Short-Term Memory),它可以避免常規RNN的梯度消失,因此在工業界得到了廣泛的應用。
影象處理八:前向對映和後向對映
影象的幾何變換:在不改變影象畫素的前提下,對影象畫素進行空間幾何變換。常見的變換:距離變換,座標對映,平移,映象,旋轉,縮放和仿射變換等等。 影象的幾何變換:建立了一種源影象畫素與
【matlab】雷達成像系列 之 BP(BackProjection,後向投影) 成像演算法
一、什麼是BP演算法? 由來:BP演算法最初是McCorkle受計算機層析技術的啟發推導而來,所謂的計算機層析:就是CT(Computer Tomograpy),這是在醫
activity啟動流程例項+設定流程變數+獲取流程變數+向後執行一步
ProcessEngine processEngine=ProcessEngines.getDefaultProcessEngine();/**部署流程定義(從inputStream)*/@Testpublic void deploymentProcess_inpustrea
python裡使用正則表示式的前向搜尋或後向搜尋模式
在許多的情況下,很多要匹配內容是一起出現,或者一起不出現的。比如《》,< >,這樣的括號,不存在使用半個的情況。因此,在正則表示式裡也有一致性的判斷,要麼兩個尖括號一起出現,要麼一個也不要