影象平滑是計算攝影學一門基礎重要的工具，其作用是拂去不重要的細節，保留較大的影象邊緣，主要應用於邊緣檢測，JPEG壓縮影象人工偽跡去除，非真實繪製等領域。

影象平滑大體上可以分為兩類：基於區域性和基於全域性方法，基於區域性的方法像有名雙邊濾波，各向異性擴散，將影象分成一些區域性塊進行處理；全域性方法比如全變分（Total Variation）和最小二乘濾波(Weighted Least Square)，同時處理整幅影象，可以達到全域性最優的目的。
以往的方法，拂去影象中去對影象細節部分也會對影象中大的邊緣進行懲罰，這樣也會導致影象中大的邊緣減弱或丟失，因此徐立等人提出使用影象L0範數平滑，該濾波器是一種基於稀疏策略的全域性平滑濾波器。
本文是對香港中文大學徐立等人所做的《Image Smoothing via L0 Gradient Minimization》的讀後筆錄，也可以看成是論文的翻譯吧。使用影象梯度L0範數平滑影象，具有以下優點：

• 通過去除小的非零梯度，撫平不重要的細節資訊
• 增強影象顯著性邊緣

影象梯度L0範數最小化

L0範數可以理解為向量中非零元素的個數。
影象梯度L0範數可以如下表示

c(f):=#{p|∣∣fp−fp−1∣∣≠0}
這裡p和p+1是影象中相鄰元素，|fp−fp−1|就是影象梯度，也即影象的前向差分，#{}表示計數，輸出影象中滿足|fp−fp−1|≠0的個數，即c(f)是影象梯度的L0範數。這樣表示有一個優點，就是c(f)是非零梯度個數的函式，與影象的梯度本身無關，也就是
#{p|∣∣fp−fp−1∣∣≠0}=#{p|∣∣α(fp−fp−1)∣∣≠0}
這還不是我們的目標函式，只是一個約束條件。

影象梯度最小化平滑

一維訊號

先以一維訊號為例，輸入訊號g

，輸出訊號f，那麼我們的目標函式可以如下表示：

minf∑p(fp−gp)2s.t.c(f)=k
左邊使得輸入訊號與輸出訊號儘可能接近，右邊非零約束梯度個數為k。下圖依次是k=1,k=2,k=5,k=200時恢復的訊號。

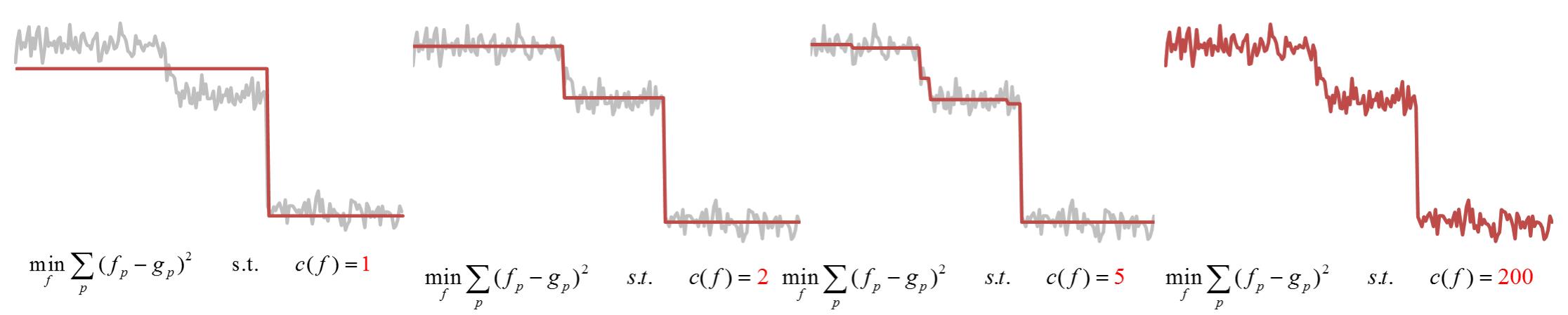
實際上，k的取值變化範圍很大，特別是對於二維影象來說。將上式子轉換成無約束問題
minf∑p(fp−gp)2+λ⋅c(f)
這裡λ是一個權重控制兩者之間的比重，實際上它是一個平滑引數，當其值越大越平滑。影象中非零梯度個數與1λ呈單調遞增關係。
從下圖中可以看到梯度L0範數的優點，即訊號的尖銳部分沒有被減弱。

二維影象

二維影象中，我們需要約束影象水平和垂直方向的梯度數目，形式上如下

minf∑p(fp−gp)2+λ⋅c(∂xf,∂yf)
c(∂xf,∂yf)=#{p|∣∣∂xfp∣∣+∣∣∂yfp∣∣≠0}
由於L0範數不可導，全域性最優問題是一個NP難問題，所以這裡使用變數分裂法，鬆弛為兩個二次規劃問題，每個問題都有其閉式解（closed-form）(因為二次函式都可以求導，得到其最小值)。
minf∑p(fp−gp)2+λ⋅c(∂xf,∂yf)+β⋅∑p((∂xfp−hp)

相關推薦

L0範數影象平滑

影象平滑是計算攝影學一門基礎重要的工具，其作用是拂去不重要的細節，保留較大的影象邊緣，主要應用於邊緣檢測，JPEG壓縮影象人工偽跡去除，非真實繪製等領域。 影象平滑大體上可以分為兩類：基於區域性和基於全域性方法，基於區域性的方法像有名雙邊濾波，各向異性

基於L0範數平滑的影象漫畫特效生成演算法

void* ImageCartoonStylizationThread(void *arg) { CartoonStylizationInfo *cartoonstylization_info = (CartoonStylizationInfo *)arg; BMPINFO *pSrcBitmap = c

機器學習中的範數規則化之（一）L0、L1與L2範數

[0 證明 基本上 復雜度 所有 img 方法 風險 機器學習 機器學習中的範數規則化之（一）L0、L1與L2範數 [email protected]/* */ http://blog.csdn.net/zouxy09 轉自：http://blog.csdn.n

『教程』L0、L1與L2範數_簡化理解

線性 實驗 tab 下一個 約束 特征 方式 等於 b2c 『教程』L0、L1與L2範數 一、L0範數、L1範數、參數稀疏 L0範數是指向量中非0的元素的個數。如果我們用L0範數來規則化一個參數矩陣W的話，就是希望W的大部分元素都是0，換句話說，讓參數W

【轉】範數規則化L0、L1與L2範數

spa http span get font lan pan href -s http://blog.csdn.net/zouxy09/article/details/24971995【轉】範數規則化L0、L1與L2範數

機器學習中的範數規則化之L0、L1與L2範數

實驗 方程 為什麽 over 大數據 來講 退回 數據庫 解釋 　　今天看到一篇講機器學習範數規則化的文章，講得特別好，記錄學習一下。原博客地址（http://blog.csdn.net/zouxy09）。 　　今天我們聊聊機器學習中出現的非常頻繁的問題：過擬合與規則化。我

深度學習-23:矩陣理論(L0/L1/L2範數)

深度學習-23:矩陣理論(L0/L1/L2範數) 深度學習原理與實踐(開源圖書)-總目錄, 建議收藏，告別碎片閱讀！ 線性代數是數學的一個分支，廣泛應用於科學和工程領域。線性代數和矩陣理論是機器學習和人工智慧的重要數學基礎。有短板的請補課，推薦《The Matrix

深度學習 --- 優化入門六（正則化、引數範數懲罰L0、L1、L2、Dropout）

      前面幾節分別從不同的角度對梯度的優化進行梳理，本節將進行正則化的梳理，所謂正則化，簡單來說就是懲罰函式，在機器學習中的SVM中引入拉格朗日乘子法即引入懲罰項解決了約束問題，在稀疏自編碼器中我們引入了懲罰因子去自動調整隱層的神經元的個數，以此達到壓縮率和失

影象處理能量泛函優化——L1範數正則化項，軟閾值公式

接上篇更新的L2範數求解的問題，接著講L1範數更新的問題 L1範數正則化項又稱為拉布拉斯先驗。帶有L1正則化項的問題是圖問題，求解相對簡單，具有閉式解。其求解就是著名的軟閾值公式。 問題

能量泛函優化方法——L2範數（應用於影象處理）

在深度學習大火的今天，熟不知以前的影象處理方法大都還是使用能量泛函優化的方法，即使是今天依然有著深度學習不可取代的魅力。要想學習，基礎的優化方法必不可少。 先說說傳統的影象處理方法包括影象超分，影象去模糊，影象去噪等，現在一些有意思的應用比如去雨、去霧、去霾、去雲等等。在深度學習之前解決這類

常用loss以及L0，L1以及L2範數

如果是Square loss，那就是最小二乘了； 如果是Hinge Loss，那就是著名的SVM了； 如果是exp-Loss，那就是牛逼的 Boosting了； 如果是log-Loss，那就是Logistic Regression了； L0範數是指向量中非0的元素的

範數正則化L0、L1、L2-嶺迴歸&Lasso迴歸（稀疏與特徵工程）

轉載自：http://blog.csdn.net/sinat_26917383/article/details/52092040 一、正則化背景 監督機器學習問題無非就是“minimizeyour error while regularizing your param

深度學習——L0、L1及L2範數

在深度學習中，監督類學習問題其實就是在規則化引數同時最小化誤差。最小化誤差目的是讓模型擬合訓練資料，而規則化引數的目的是防止模型過分擬合訓練資料。 引數太多，會導致模型複雜度上升，容易過擬合，也就是訓練誤差小，測試誤差大。因此，我們需要保證模型足夠簡單，並在此基礎上訓練誤差小，這樣訓練得到的引數

機器學習中的範數規則化之 L0、L1與L2範數

       今天我們聊聊機器學習中出現的非常頻繁的問題：過擬合與規則化。我們先簡單的來理解下常用的L0、L1、L2和核範數規則化。最後聊下規則化項引數的選擇問題。這裡因為篇幅比較龐大，為了不嚇到大家，我將這個五個部分分成兩篇博文。知識有限，以下都是我一些淺顯的

機器學習中正則懲罰項L0/L1/L2範數詳解

https://blog.csdn.net/zouxy09/article/details/24971995 原文轉自csdn部落格，寫的非常好。 L0: 非零的個數 L1: 引數絕對值的和 L2:引數平方和

關於L0，L1和L2範數的規則化

本文主要整理一下機器學習中的範數規則化學習的內容： 規則化 -什麼是規則化 -為什麼要規則化 -規則化的理解 -怎麼規則化 -規則化的作用 範數 -L0範數和L1範數 -L2範數 -L1範數和L2範數 補充 -condition numbe

機器學習中的規則化範數(L0, L1, L2, 核範數)

目錄： 三、核範數 今天我們聊聊機器學習中出現的非常頻繁的問題：過擬合與規則化。我們先簡單的來理解下常用的L0、L1、L2和核範數規則化。最後聊下規則化項引數的選擇問題。這裡因為篇幅比較龐大，為了不嚇到大家，我將這個五個部分分成兩篇博文。知識有限，以下都是我一些淺顯的看法，如果理解存在錯誤，希望大

轉：機器學習中的範數規則化之（一）L0、L1與L2範數

今天我們聊聊機器學習中出現的非常頻繁的問題：過擬合與規則化。我們先簡單的來理解下常用的L0、L1、L2和核範數規則化。最後聊下規則化項引數的選擇問題。這裡因為篇幅比較龐大，為了不嚇到大家，我將這個五個部分分成兩篇博文。知識有限，以下都是我一些淺顯的看法，如果理解存在錯誤

L0、L1、L2範數與核範數（二）

OK，回到問題本身。我們選擇引數λ的目標是什麼？我們希望模型的訓練誤差和泛化能力都很強。這時候，你有可能還反映過來，這不是說我們的泛化效能是我們的引數λ的函式嗎？那我們為什麼按優化那一套，選擇能最大化泛化效能的λ呢？Oh，sorry to tell you that，因為泛化效能並不是λ的簡單的函式！它具有很

轉載：機器學習中的範數規則化之（一）L0、L1與L2範數

監督機器學習問題無非就是“minimizeyour error while regularizing your parameters”，也就是在規則化引數的同時最小化誤差。最小化誤差是為了讓我們的模型擬合我們的訓練資料，而規則化引數是防止我們的模型過分擬合我們的訓練資料。多麼