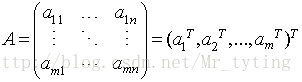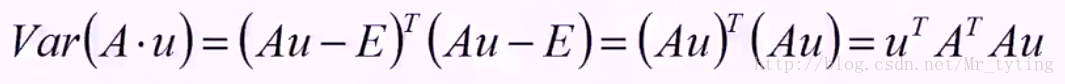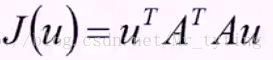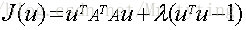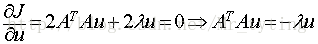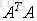機器學習-->特徵降維方法總結
本篇博文主要總結一下機器學習裡面特徵降維的方法,以及各種方法之間的聯絡和區別。
機器學習中我個人認為有兩種途徑可以來對特徵進行降維,一種是特徵抽取,其代表性的方法是PCA,SVD降維等,另外一個途徑就是特徵選擇。
特徵抽取
先詳細講下PCA降維的原理
對於n個特徵的m個樣本,將每個樣本寫成行向量,得到矩陣A
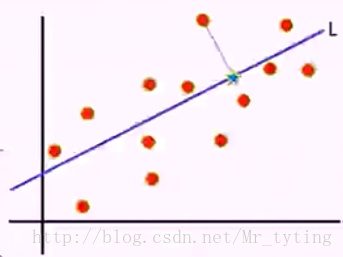
尋找樣本的主方向u:將m個樣本值投影到某個直線L上,得到m個位於直線L上的點,計算m個投影點的方差。認為方差最大的直線方向就是主方向。那麼如何選取到方差最大的直線方向呢?
我們這裡假定樣本是中心化的,若是沒有去均值化,則計算m個樣本的均值,將樣本真實值減去均值。
我們取投影直線L的延伸方向為u,u即為投影方向,計算矩陣A乘以方向向量u的值得:
然後求向量A*u的方差,即計算投影以後的方差:
方差的計算公式為: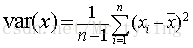
那麼其目標函式即為:
回到目標本身,就是要找一個方向u使得方差最大,也就是使得上述的目標函式最大。u是個方向向量,可以加上一個約束條件,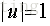
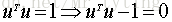
要使得目標函式最大,那麼需要對u求偏導得:
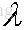
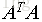
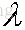
注意矩陣A表示的是n個特徵的m個樣本,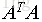
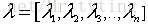
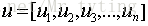 為其對應的特徵向量(投影方向)且相互正交,我們把特徵值從大到小排序,這裡我們假設
為其對應的特徵向量(投影方向)且相互正交,我們把特徵值從大到小排序,這裡我們假設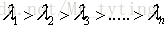 ,那麼我們可以認為
,那麼我們可以認為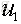 這個方向是最主要的方向(主分),
這個方向是最主要的方向(主分),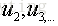 其次。可以自定的選擇幾個主分,那麼就取幾個最主要的方向作為投影方向。
其次。可以自定的選擇幾個主分,那麼就取幾個最主要的方向作為投影方向。
通過以上的分析可以得出,PCA其實就是尋找一個或幾個投影方向,使得樣本值投影以後方差最大。這種投影可以理解對特徵的重構或者是組合。
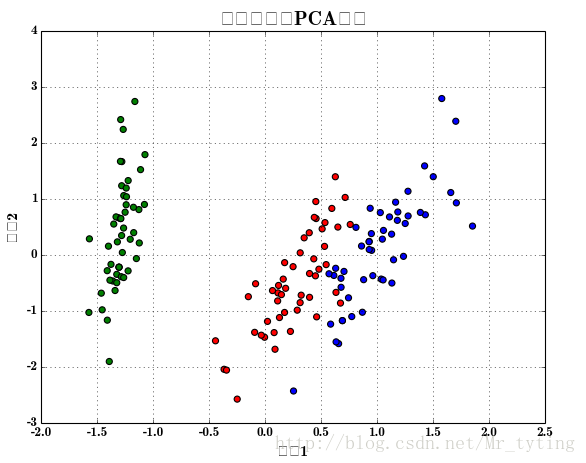
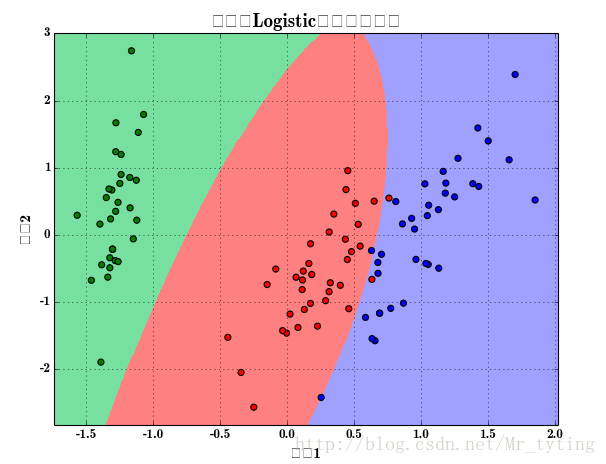
利用PC降維將特徵從四維降為二維,並且用多項式進行特徵衍生,然後用邏輯迴歸進行分類,並畫出分類後的效果圖。
# -*- coding:utf-8 -*-
import pandas as pd
import numpy as np
from sklearn.decomposition import 樣本散點圖:
分類後的效果圖:
而SVD降維就是對樣本特徵矩陣進行奇異值分解,來得出最主要的成分。有關SVD降維的更詳細內容可以檢視我的另外一篇博文機器學習–>矩陣和線性代數裡相關內容。
特徵選擇
關於特徵選擇的詳細內容可以檢視我的另外一篇博文sklearn特徵選擇。
總結
特徵抽取,特徵選擇都能達到降維的效果,那麼他們之間有什麼區別呢?我個人覺得特徵抽取是對所有特徵進行了組合,或者說是線性變換,或者說是投影,選擇出最好的或者是效果最好的幾個投影方向(變換方式),既保證了資訊最大程度的保留,又使維度降低了。而特徵選擇只是單純的根據某個標準,對特徵的重要程度進行了計算,保留最靠前的,最重要的一些特徵,剔除剩下的不重要的特徵。
無論是特徵抽取還是特徵選擇,都有資訊的丟失,但是他們都是丟失一些相對來說不重要的資訊,保留他們認為重要的資訊。
相關推薦
機器學習-->特徵降維方法總結
本篇博文主要總結一下機器學習裡面特徵降維的方法,以及各種方法之間的聯絡和區別。 機器學習中我個人認為有兩種途徑可以來對特徵進行降維,一種是特徵抽取,其代表性的方法是PCA,SVD降維等,另外一個途徑就是特徵選擇。 特徵抽取 先詳細講下PCA降維的原理
機器學習四大降維方法
引言: 機器學習領域中所謂的降維就是指採用某種對映方法,將原高維空間中的資料點對映到低維度的空間中。降維的本質是學習一個對映函式 f : x->y,其中x是原始資料點的表達,目前最多使用向量表達形式。 y是資料點對映後的低維向量表達,通常y的維度小於x的維度(當然提高維度也是可以的)。f可能是顯
一、降維——機器學習筆記——降維(特徵提取)
目錄 2、示例 一、為什麼要降維 維數災難:在給定精度下,準確地對某些變數的函式進行估計,所需樣本量會隨著樣本維數的增加而呈指數形式增長。 降維的意義:克服維數災難,獲取本質特徵,節省儲存空間,去除無用噪聲,實現資料視覺化
機器學習—PCA降維
one 因此 表示 實現 維度 非監督學習 衡量 取出 計算方法 1、基本思想: 主成分分析(Principal components analysis,以下簡稱PCA)是最重要的降維方法之一。在數據壓縮消除冗余和數據噪音消除等領域都有廣泛的應用。 PCA顧名思義,
機器學習——資料降維
特徵選擇 選擇特徵就是單純地從提取到的所有特徵種選擇部分特徵作為訓練集特徵,特徵在選擇前和選擇後可以改變值,也不改變值,但是選擇後的特徵維度肯定比選擇前小,畢竟我們只選擇了其中的一部分特徵。 主要方法(三大武器):Filter(過濾器):VarianceThreshold
BAT機器學習特徵工程工作經驗總結(一)如何解決資料不平衡問題(附python程式碼)
很多人其實非常好奇BAT裡機器學習演算法工程師平時工作內容是怎樣?其實大部分人都是在跑資料,各種map-reduce,hive SQL,資料倉庫搬磚,資料清洗、資料清洗、資料清洗,業務分析、分析case、找特徵、找特徵…而複雜的模型都是極少數的資料科學家在做。例
機器學習演算法--降維技術
當資料集維數較高時,往往會出現樣本稀疏以及距離難以計算等問題,而某個學習任務可能僅與資料的某個低維分佈有關,因此可以採用降維技術來變換資料空間座標系,主要有: LDA線性判別分析 PCA主成分分析 ICA獨立成分分析 FA因子分析 SVD奇異值分解 維數災難:資
python大戰機器學習——資料降維
注:因為公式敲起來太麻煩,因此本文中的公式沒有呈現出來,想要知道具體的計算公式,請參考原書中內容 降維就是指採用某種對映方法,將原高維空間中的資料點對映到低維度的空間中 1、主成分分析(PCA) 將n維樣本X通過投影矩陣W,轉換為K維矩陣Z 輸入:樣本集D,低維空間d 輸出:投影矩陣W
機器學習-PCA降維與DBScan聚類分析實戰
基本概念: 在資料處理中,經常會遇到特徵維度比樣本數量多得多的情況,如果拿到實際工程中去跑,效果不一定好。一是因為冗餘的特徵會帶來一些噪音,影響計算的結果;二是因為無關的特徵會加大計算量,耗費時間和資源。所以我們通常會對資料重新變換一下,再跑模型。資料變換的目的不僅僅是降維,還可以消除特徵之間的相關性,
機器學習筆記——降維(dimensionality reduction)
降維 目的 我們對資料進行降維的目的有兩個:一個是資料壓縮,對於資料壓縮我們可以大大地節省儲存空間 第二就是使得資料可以視覺化,我們將多維資料壓縮成二維可以供我們更好地觀察資料的特徵 主成分分析(PAC) 主成分分析法可以將n維的資料降為k維,實際上我們是選取了一個k
機器學習 -- > 檢測異常樣本方法總結
資料預處理的好壞,很大程度上決定了模型分析結果的好壞。其中,異常值(outliers)檢測是整個資料預處理過程中,十分重要的一環。方法也是多種多樣。 由於異常值檢驗,和去重、缺失值處理不同,它帶有一定的主觀性。在實際業務場景中,我們要根據具體的業務邏輯來判別哪
機器學習:降維演算法-主成分分析PCA演算法兩種角度的推導
若把高維空間的樣本點(可以想象是一個3維的)對映到一個超平面,怎樣的超平面可以認為是“好的”,可以想到這個超平面大概有這樣的性質: 最近重構行:樣本點到超平面的距離都足夠近;(樣本點變化儘可能小,丟失的資訊儘可能少) 最大可分性:樣本點在這個超平面上的投影儘可能分開.(樣
機器學習筆記簿 降維篇 LDA 01
機器學習中包含了兩種相對應的學習型別:**無監督學習**和**監督學習**。**無監督學習**指的是讓機器只從資料出發,挖掘資料本身的特性,對資料進行處理,PCA就屬於無監督學習,因為它只根據資料自身來構造投影矩陣。而**監督學習**將使用資料和資料對應的標籤,我們希望機器能夠學習到資料和標籤的關係,例如分類
機器學習實踐(五)—sklearn之特徵降維
一、特徵降維概述 為什麼要對特徵進行降維處理 如果特徵本身存在問題或者特徵之間相關性較強,對於演算法學習預測會影響較大 什麼是降維 降維是指在某些限定條件下,降低隨機變數(特徵)個數,得到一組“不
機器學習四大資料降維方法詳解
引言: 機器學習領域中所謂的降維就是指採用某種對映方法,將原高維空間中的資料點對映到低維度的空間中。降維的本質是學習一個對映函式 f : x->y,其中x是原始資料點的表達,目前最多使用向量表達形式。 y是資料點對映後的低維向量表達,通常y的維度小於x的維度(當然提高維度也是可以的)。f可能是顯
淺析機器學習中的降維方法
在我們用機器學習去訓練資料集的時候,可能會遇到上千甚至上萬個特徵,隨著資料量的增大,所分析出結果的準確度雖然會提高很多,但同時處理起來也會變得十分棘手,此時我們不得不想出一種方法去減少特徵將高維的資料轉化為低維的資料(降維)。 什麼是降維? 簡單的說降維就是把一個n維的資
機器學習特徵選擇方法
有一句話這麼說,特徵決定上限,模型逼近上限。特徵選擇對後面的模型訓練很重要,選擇合適重要的特徵,對問題求解尤為重要,下面介紹一些常見的特徵選擇方法。 通常來說,從兩個方面考慮來選擇特徵: 特徵是否發散:如果一個特徵不發散,例如方差接近於0,也就是說樣本在這個特徵上基本上沒有差異,這個
機器學習特徵工程總結
一、前言 資料清洗: 不可信的樣本去除 缺失值極多的欄位考慮去除 補齊缺失值 資料取樣:很多情況下,正負樣本是不均衡的,大多數模型對正負樣本是敏感的(比如LR) 正樣本>>負樣本,且量都挺大:下采樣 正樣本>>負
機器學習之多維縮放(MDS)降維
機器學習之多維縮放(MDS)降維 # -*- coding: utf-8 -*- """ Created on Mon Nov 26 17:25:11 2018 @author: muli """ import numpy as np import matplotl
2018最新實用BAT機器學習演算法崗位系列面試總結(結構化資料特徵工程)
特徵工程,是對原始資料進行一系列工程處理,目的是去除原始資料中的雜質和冗餘,設計更高效的特徵來描述求解的問題與預測模型之間的關係。 特徵工程主要對以下兩種常用的資料型別做處理: (1)結構化資料。結構化資料型別可以看作關係型資料庫的一張表,每列都有清晰的定義,包