2. 程式人生 > >機器學習 -- > 檢測異常樣本方法總結

機器學習 -- > 檢測異常樣本方法總結

阿新 • • 發佈：2019-01-04

資料預處理的好壞，很大程度上決定了模型分析結果的好壞。其中，異常值（outliers）檢測是整個資料預處理過程中，十分重要的一環。方法也是多種多樣。

由於異常值檢驗，和去重、缺失值處理不同，它帶有一定的主觀性。在實際業務場景中，我們要根據具體的業務邏輯來判別哪些樣本是離群點。

下面總結下我平時經常用到的異常樣本檢測方法，可能總結的不全。

視覺化的方法

對於樣本集某一個特徵而言，可以直接畫出這個樣本集在這個特徵上值的分佈情況，如果有一些資料明顯過高或者過低，則可以視其為異常樣本去掉即可。

概率統計的方法

基於正態分佈的一元離群點檢測方法

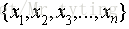
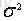假設有 n 個點這裡寫圖片描述，那麼可以計算出這 n 個點的均值這裡寫圖片描述

和方差這裡寫圖片描述。均值和方差分別被定義為：


這裡寫圖片描述

在正態分佈的假設下，區域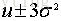這裡寫圖片描述 包含了99.7% 的資料，如果某個值距離分佈的均值 這裡寫圖片描述 超過了這裡寫圖片描述，那麼這個值就可以被簡單的標記為一個異常點（outlier）。

基於一元正態分佈的離群點檢測方法

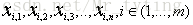
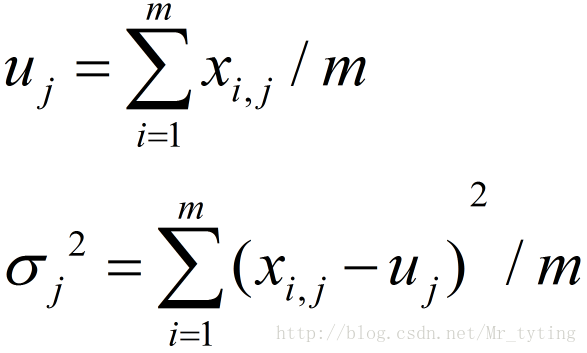
假設 n 維的資料集合形如 這裡寫圖片描述 ,即有m個樣本，n個特徵。那麼可以計算每個維度的均值和方差 這裡寫圖片描述。那麼可以計算每個特徵的平均值和方差：


這裡寫圖片描述

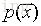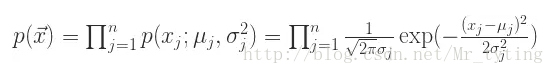
在正態分佈的假設下，如果有一個新的資料 這裡寫圖片描述，可以計算概率 這裡寫圖片描述如下：

這裡寫圖片描述

根據概率值的大小就可以判斷 x 是否屬於異常值。

多元高斯分佈的異常點檢測

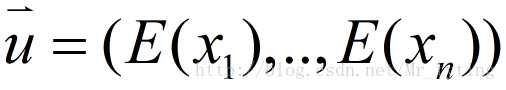
假設 n 維的資料集合這裡寫圖片描述 ，可以計算 n 維的均值向量：


這裡寫圖片描述

和 n*n 的協方差矩陣：


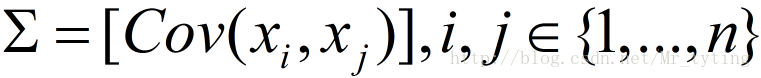
這裡寫圖片描述

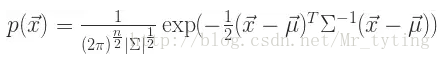
如果有一個新的資料這裡寫圖片描述，可以計算：

這裡寫圖片描述

使用 Mahalanobis 距離檢測多元離群點

對於一個多維的資料集合 D，假設 這裡寫圖片描述是均值向量，那麼對於資料集 D 中的其他物件 a，從 a 到 這裡寫圖片描述的 Mahalanobis 距離是：


這裡寫圖片描述

其中 S 是協方差矩陣。

在這裡，這裡寫圖片描述 是數值，可以對這個數值進行排序，如果數值過大，那麼就可以認為點 a 是離群點。或者對一元實數集合 這裡寫圖片描述進行離群點檢測，如果 這裡寫圖片描述 被檢測為異常點，那麼就認為 a 在多維的資料集合 D 中就是離群點。

特徵是二維時，用馬氏距離檢查異常值：

#coding:utf-8

from
 
 numpy import float64
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
from scipy.spatial import distance
from pandas import Series

Height_cm = np.array([164, 167, 168, 169, 169, 170, 170, 170, 171, 172, 172, 173, 173, 175, 176, 178], dtype=float64)
Weight_kg = np.array([54,  57,  58,  60,  61,  60,  61,  62,  62,  64,  62,  62,  64,  56,  66,  70], dtype=float64)
hw = {'Height_cm': Height_cm, 'Weight_kg': Weight_kg}
hw = pd.DataFrame(hw)


n_outliers = 2##這裡只檢測兩個異常值
## 計算每個樣本的馬氏距離，並且從大到小排序，越大則越有可能是離群點,返回其索引
m_dist_order = Series([float(distance.mahalanobis(hw.iloc[i], hw.mean(), np.mat(hw.cov().as_matrix()).I) ** 2)
                        for i in range(len(hw))]).sort_values(ascending=False).index.tolist()

is_outlier = [False, ] * 16 ##返回長度為16的全FALSE的列表
for i in range(n_outliers):## n_outliers = 2,找出馬氏距離最大的兩個樣本，標記為True,為離群點
    is_outlier[m_dist_order[i]] = True


color = ['g', 'black']
pch = [1 if is_outlier[i] == True else 0 for i in range(len(is_outlier))]
cValue = [color[is_outlier[i]] for i in range(len(is_outlier))]
fig = plt.figure()
plt.title('Scatter Plot')
plt.xlabel('Height_cm')
plt.ylabel('Weight_kg')
plt.scatter(hw['Height_cm'], hw['Weight_kg'], s=40, c=cValue)
plt.show()

這裡寫圖片描述
很好的識別出兩個異常值。

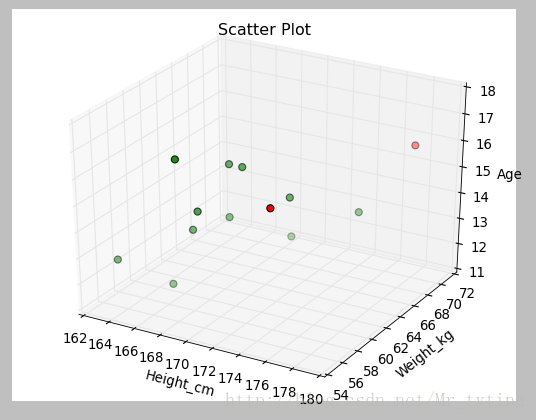
當特徵是三維時，用馬氏距離檢查異常值：

#coding:utf-8

import pandas as pd
from sklearn import preprocessing
import numpy as np
from numpy import float64
from matplotlib import pyplot as plt
from scipy.spatial import distance
from pandas import Series
import mpl_toolkits.mplot3d

Height_cm = np.array([164, 167, 168, 168, 169, 169, 169, 170, 172, 173, 175, 176, 178], dtype=float64)
Weight_kg = np.array([55,  57,  58,  56,  57,  61,  61,  61,  64,  62,  56,  66,  70], dtype=float64)
Age = np.array([13,  12,  14,  17,  15,  14,  16,  16,  13,  15,  16,  14,  16], dtype=float64)
hw = {'Height_cm': Height_cm, 'Weight_kg': Weight_kg, 'Age': Age}
hw = pd.DataFrame(hw)

n_outliers = 2

m_dist_order =  Series([float(distance.mahalanobis(hw.iloc[i], hw.mean(), np.mat(hw.cov().as_matrix()).I) ** 2)
                        for i in range(len(hw))]).sort_values(ascending=False).index.tolist()
is_outlier = [False, ] * 13
for i in range(n_outliers):
    is_outlier[m_dist_order[i]] = True
# print is_outlier

color = ['g', 'r']
pch = [1 if is_outlier[i] == True else 0 for i in range(len(is_outlier))]
cValue = [color[is_outlier[i]] for i in range(len(is_outlier))]
# print cValue

fig = plt.figure()
ax1 = plt.subplot(111, projection='3d')
ax1.set_title('Scatter Plot')
ax1.set_xlabel('Height_cm')
ax1.set_ylabel('Weight_kg')
ax1.set_zlabel('Age')
ax1.scatter(hw['Height_cm'], hw['Weight_kg'], hw['Age'],  s=40, c=cValue)
plt.show()

##除去20％的異常樣本，輸出剩餘80％的樣本
percentage_to_remove = 20#除去20%的異常樣本
number_to_remove = round(len(hw) * percentage_to_remove / 100)   # 四捨五入取整
rows_to_keep_index = m_dist_order[int(number_to_remove): ]
my_dataframe = hw.loc[rows_to_keep_index]
print my_dataframe

這裡寫圖片描述

注意：當你的資料表現出非線性關係關係時，你可要謹慎使用該方法了，馬氏距離僅僅把他們作為線性關係處理。例如上面的身高和體重的關係，按常識，身高和體重必然存線上性關係所以馬氏距離能很好的檢測到異常值，但是是如果是非線性關係就得謹慎使用馬氏距離了。

使用這裡寫圖片描述 統計量檢測多元離群點

在正態分佈的假設下，這裡寫圖片描述 統計量可以用來檢測多元離群點。對於某個物件 a，這裡寫圖片描述統計量是：


這裡寫圖片描述

其中， 這裡寫圖片描述是a在第 i 維上的取值，這裡寫圖片描述是所有物件在第 i 維的均值，n 是維度。如果物件 a 的 這裡寫圖片描述統計量很大，那麼該物件就可以認為是離群點。

PCA除去異常值

PCA對高維資料進行降維，其中降維是目的，最大方差是手段。其實就是保留效果最好的一個或最好的前幾個相互正交的投影方向，使得樣本值投影以後方差最大。這種投影可以理解對特徵的重構或者是組合，其降維的結果往往是去除了異常值。

PCA原理請看我的另外一篇博文：PCA

iForest （Isolation Forest）孤立森林 異常檢測

iForest屬於Non-parametric和unsupervised的方法，即不用定義數學模型也不需要有標記的訓練。對於如何查詢哪些點是否容易被孤立（isolated），iForest使用了一套非常高效的策略。假設我們用一個隨機超平面來切割（split）資料空間（data space）, 切一次可以生成兩個子空間（想象拿刀切蛋糕一分為二）。之後我們再繼續用一個隨機超平面來切割每個子空間，迴圈下去，直到每子空間裡面只有一個數據點為止。直觀上來講，我們可以發現那些密度很高的簇是可以被切很多次才會停止切割，但是那些密度很低的點很容易很早的就停到一個子空間了。

怎麼來切這個資料空間是iForest的設計核心思想。由於切割是隨機的，所以需要用ensemble的方法來得到一個收斂值，即反覆從頭開始切，然後平均每次切的結果。iForest 由t個iTree（Isolation Tree）孤立樹 組成，每個iTree是一個二叉樹結構，其實現步驟如下：

  1. 從訓練資料中隨機選擇Ψ個點樣本點作為subsample，放入樹的根節點。

  2. 隨機指定一個維度（attribute），在當前節點資料中隨機產生一個切割點p——切割點產生於當前節點資料中指定維度的最大值和最小值之間。

  3. 以此切割點生成了一個超平面，然後將當前節點資料空間劃分為2個子空間：把指定維度裡小於p的資料放在當前節點的左孩子，把大於等於p的資料放在當前節點的右孩子。

  4. 在孩子節點中遞迴步驟2和3，不斷構造新的孩子節點，直到 孩子節點中只有一個數據（無法再繼續切割） 或 孩子節點已到達限定高度 。

然後在生成的iForest內計算：

  1. 計算iTree中樣本x從根到葉子的長度f(x)。
  2. 計算iForest中f(x)的總和F(x) 。

異常檢測：若樣本x為異常值，它應在大多 數iTree中很快從根到達葉子，即F(x)較小。

sklearn中的iForest:

sklearn.ensemble.IsolationForest(n_estimators=100, max_samples=’auto’, contamination=0.1, max_features=1.0, bootstrap=False, n_jobs=1, random_state=None, verbose=0)

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForest

rng = np.random.RandomState(42)

# Generate train data
X = 0.3 * rng.randn(100, 2)
X_train = np.r_[X + 2, X - 2]##按行堆疊，shape(200,2)
# Generate some regular novel observations
X = 0.3 * rng.randn(20, 2)
X_test = np.r_[X + 2, X - 2]##按行堆疊，shape(40,2)
# Generate some abnormal novel observations
X_outliers = rng.uniform(low=-4, high=4, size=(20, 2))##shape(20,2)

# fit the model
clf = IsolationForest(max_samples=100, random_state=rng)
clf.fit(X_train)##　訓練出一個iForest，iForest為無監督的方法，但是也不能直接對無標記樣本集預測，可以先fit無標記樣本集，然後在predict
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)

# plot the line, the samples, and the nearest vectors to the plane
xx, yy = np.meshgrid(np.linspace(-5, 5, 50), np.linspace(-5, 5, 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])##按列堆疊shape(100,2)，並且得出決策邊界
Z = Z.reshape(xx.shape)

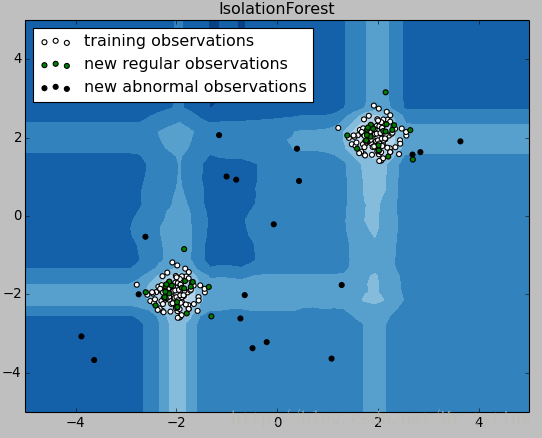
plt.title("IsolationForest")
plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)##畫出決策邊界，不同的區域顏色不同

b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white',
                 s=20, edgecolor='k')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='green',
                 s=20, edgecolor='k')
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='red',
                s=20, edgecolor='k')
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([b1, b2, c],
           ["training observations",
            "new regular observations", "new abnormal observations"],
           loc="upper left")
plt.show()

這裡寫圖片描述

由畫出的結果可知，顯然黑色樣本離群較大，應該屬於異常值，決策邊界也很好的將其劃分出來了。那我現在把識別出來的異常值去掉看看效果如何？

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForest

rng = np.random.RandomState(42)

# Generate train data
X = 0.3 * rng.randn(100, 2)
X_train = np.r_[X + 2, X - 2]
# Generate some regular novel observations
X = 0.3 * rng.randn(20, 2)
X_test = np.r_[X + 2, X - 2]
print X_test.shape
# Generate some abnormal novel observations
X_outliers = rng.uniform(low=-4, high=4, size=(20, 2))
print X_outliers.shape

# fit the model
clf = IsolationForest(max_samples=100, random_state=rng)
clf.fit(X_train)
y_pred_train = clf.predict(X_train)## 對樣本的預測結果為1則說明為正常值，為-1表示為異常值

train_index=[]
for i,j in enumerate(y_pred_train):
    if j==1:
        train_index.append(i)## 獲取所有正常值的索引


test_index=[]
y_pred_test = clf.predict(X_test)
for i,j in enumerate(y_pred_test):
    if j==1:
        test_index.append(i)



y_pred_outliers = clf.predict(X_outliers)
outliers_index=[]
for i,j in enumerate(y_pred_outliers):
    if j==1:
        outliers_index.append(i)


new_x_train=X_train[train_index]##將所有預測為正常樣本重新組成新的樣本集
new_x_test=X_test[test_index]
new_x_outliers=X_outliers[outliers_index]


# plot the line, the samples, and the nearest vectors to the plane
xx, yy = np.meshgrid(np.linspace(-5, 5, 50), np.linspace(-5, 5, 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.title("IsolationForest")
plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)

## 畫出各個樣本集的正常值分佈情況
b1 = plt.scatter(new_x_train[:, 0], new_x_train[:, 1], c='white',
                 s=20, edgecolor='k')
b2 = plt.scatter(new_x_test[:, 0], new_x_test[:, 1], c='green',
                 s=20, edgecolor='k')
c = plt.scatter(new_x_outliers[:, 0], new_x_outliers[:, 1], c='black',
                s=20, edgecolor='k')
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([b1, b2, c],
           ["training observations",
            "new regular observations", "new abnormal observations"],
           loc="upper left")
plt.show()

這裡寫圖片描述

顯然去掉的樣本的確為異常值。

Local Outlier Factor

neighbors.LocalOutlierFactor（LOF）演算法用來計算觀測樣本異常程度的分數（稱為區域性離群因子）。是一種無監督方法。它測量給定資料點相對於其鄰居的區域性密度　偏差。這個演算法就是檢測那些周圍密度比較低的樣本，然後將他們標記為離群點。

實際上，從k個最近的鄰居獲得區域性密度。觀察的LOF得分等於他的k個最近鄰居的平均區域性密度與其本地密度的比值：正常樣本預計具有與其鄰居類似的區域性密度，而異常樣本的區域性密度預計要比其鄰居的區域性密度小得多。

鄰居的數量k的選擇是個需要考慮的問題，通常k = 20時總體上很好地工作。當異常值的比例很高時k應該更大。

LOF演算法的優點在於它考慮了資料集的本地和全域性屬性：即使在異常樣本具有不同基礎密度的資料集中，它也能很好地執行。問題不在於，樣本是如何孤立的，而是與周圍鄰居的隔離程度。

#coding:utf-8

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor

np.random.seed(42)

# Generate train data
X = 0.3 * np.random.randn(100, 2)
# Generate some abnormal novel observations
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
X = np.r_[X + 2, X - 2, X_outliers]##　行連線 shape(220,2)


# fit the model
clf = LocalOutlierFactor(n_neighbors=20)
y_pred = clf.fit_predict(X)## 預測為1則為正常樣本，-1為異常樣本
outlier=[]
for i,j in enumerate(y_pred):
    if j==1:
        outlier.append(i)##　獲取所有正常樣本

y_pred_outliers = y_pred[200:]

# plot the level sets of the decision function
xx, yy = np.meshgrid(np.linspace(-5, 5, 50), np.linspace(-5, 5, 50))
Z = clf._decision_function(np.c_[xx.ravel(), yy.ravel()])##　畫出決策邊界
Z = Z.reshape(xx.shape)

### 畫出正常樣本和異常樣本分佈
plt.subplot(211)
plt.title("Local Outlier Factor (LOF)")
plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)##決策出不同區域用不同顏色

a = plt.scatter(X[:200, 0], X[:200, 1], c='white',
                edgecolor='k', s=20)
b = plt.scatter(X[200:, 0], X[200:, 1], c='red',
                edgecolor='k', s=20)
plt.legend([a, b],
           ["normal observations",
            "abnormal observations"],
           loc="upper left")

### 畫出去除LOF預測為異常樣本後剩下的樣本分佈
plt.subplot(212)
plt.title("remove noise samples")
plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)##決策出不同區域用不同顏色
plt.scatter(X[:200, 0], X[:200, 1], c='white',edgecolor='k', s=20)

plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))

plt.show()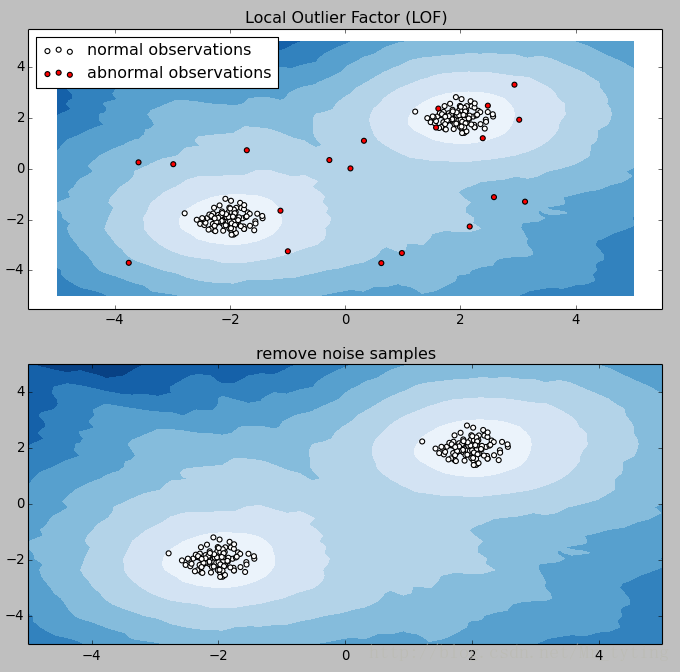

這裡寫圖片描述

顯然在這個資料集中很好的去除了異常樣本。

DBSCAN演算法識別異常樣本

可以利用聚類中的DBSCAN演算法來檢測異常，具體原理請看我的博文 機器學習–>無監督學習–>聚類裡面相關介紹。

#coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler


def expand(a, b):
    d = (b - a) * 0.1
    return a-d, b+d


if __name__ == "__main__":
    N = 1000
    centers = [[1, 2], [-1, -1], [1, -1], [-1, 1]]
    data, y = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=[0.5, 0.25, 0.7, 0.5], random_state=0)
    data = StandardScaler().fit_transform(data)
    # 資料1的引數：(epsilon, min_sample)
    params = ((0.2, 5), (0.2, 10), (0.2, 15), (0.3, 5), (0.3, 10), (0.3, 15))

    # 資料2
    # t = np.arange(0, 2*np.pi, 0.1)
    # data1 = np.vstack((np.cos(t), np.sin(t))).T
    # data2 = np.vstack((2*np.cos(t), 2*np.sin(t))).T
    # data3 = np.vstack((3*np.cos(t), 3*np.sin(t))).T
    # data = np.vstack((data1, data2, data3))
    # # # 資料2的引數：(epsilon, min_sample)
    # params = ((0.5, 3), (0.5, 5), (0.5, 10), (1., 3), (1., 10), (1., 20))

    matplotlib.rcParams['font.sans-serif'] = [u'Droid Sans Fallback']
    matplotlib.rcParams['axes.unicode_minus'] = False

    plt.figure(figsize=(12, 8), facecolor='w')
    plt.suptitle(u'DBSCAN聚類', fontsize=20)

    for i in range(6):
        eps, min_samples = params[i]
        model = DBSCAN(eps=eps, min_samples=min_samples)
        model.fit(data)
        y_hat = model.labels_

        core_indices = np.zeros_like(y_hat, dtype=bool)
        core_indices[model.core_sample_indices_] = True

        y_unique = np.unique(y_hat)
        n_clusters = y_unique.size - (1 if -1 in y_hat else 0)## y_hat=-1為聚類後的噪聲類
        print y_unique, '聚類簇的個數為：', n_clusters


        plt.subplot(2, 3, i+1)
        clrs = plt.cm.Spectral(np.linspace(0, 0.8, y_unique.size))##指定聚類後每類的顏色
        print clrs
        for k, clr in zip(y_unique, clrs):
            cur = (y_hat == k)
            if k == -1:##-1為異常樣本
                plt.scatter(data[cur, 0], data[cur, 1], s=20, c='black')##　畫出異常樣本點
                continue
            plt.scatter(data[cur, 0], data[cur, 1], s=30, c=clr, edgecolors='k')
            #plt.scatter(data[cur & core_indices][:, 0], data[cur & core_indices][:, 1], s=60, c=clr, marker='o', edgecolors='k')
        x1_min, x2_min = np.min(data, axis=0) ## 兩列的最小值
        x1_max, x2_max = np.max(data, axis=0)## 兩列的最大值
        x1_min, x1_max = expand(x1_min, x1_max)
        x2_min, x2_max = expand(x2_min, x2_max)
        plt.xlim((x1_min, x1_max))
        plt.ylim((x2_min, x2_max))
        plt.grid(True)
        plt.title(ur'$\epsilon$ = %.1f  m = %d，聚類數目：%d' % (eps, min_samples, n_clusters), fontsize=16)
    plt.tight_layout()
    plt.subplots_adjust(top=0.9)
    plt.show()

上述程式碼中，我們為DBSCAN選用了六組引數，畫出在這六組引數下，對樣本集聚類情況，並且識別出離群樣本。離群樣本為下圖中的黑色原點。


這裡寫圖片描述

在不同的引數下識別離群樣本準備程度不一樣。

那我們現在去掉這些識別出的黑色樣本看看效果如何？

這裡寫圖片描述

感覺清爽多了！並且有上圖可以看出引數選擇(0.2,15)時，聚類效果最好。

根據特徵重要性檢測異常樣本

我們可以利用基於樹的模型，比如xgboost，gbdt等訓練模型得出特徵的重要性排名，我們選取最重要的前k個特徵，如果樣本在這k個特徵中缺失很多，那麼我們可以認為這個樣本是異常樣本，是離群點。因為這個樣本對整體模型的建立沒有幫助，如果強行對其缺失值填充可能會引入噪聲。

相關推薦

機器學習 -- > 檢測異常樣本方法總結

資料預處理的好壞，很大程度上決定了模型分析結果的好壞。其中，異常值（outliers）檢測是整個資料預處理過程中，十分重要的一環。方法也是多種多樣。 由於異常值檢驗，和去重、缺失值處理不同，它帶有一定的主觀性。在實際業務場景中，我們要根據具體的業務邏輯來判別哪

用機器學習檢測異常點選流

本文內容是我學習ML時做的一個練手專案，描述應用機器學習的一般步驟。該專案的目標是從點選流資料中找出惡意使用者的請求。點選流資料長下圖這樣子，包括請求時間、IP、平臺等特徵： 該專案從開始做到階段性完成，大致可分為兩個階段：演算法選擇和工程優化。演算法選擇階段挑選合適的ML模型，嘗試了神經網路、高斯

機器學習-->特徵降維方法總結

本篇博文主要總結一下機器學習裡面特徵降維的方法，以及各種方法之間的聯絡和區別。 機器學習中我個人認為有兩種途徑可以來對特徵進行降維，一種是特徵抽取，其代表性的方法是PCA,SVD降維等，另外一個途徑就是特徵選擇。 特徵抽取 先詳細講下PCA降維的原理

吳恩達老師機器學習筆記異常檢測（一）

明天就要開組會了，天天在辦公室划水都不知道講啥。。。 今天開始異常檢測的學習，同樣程式碼比較簡單一點 異常檢測的原理就是假設樣本的個特徵值都呈高斯分佈，選擇分佈較離散的樣本的作為異常值。這裡主要注意的是通過交叉驗證對閾值的選擇和F1score的應用。 原始資料： 程式碼如下：

吳恩達老師機器學習筆記異常檢測（二）

明天就要開組會了，天天在辦公室划水都不知道講啥。。。 今天開始異常檢測的學習，同樣程式碼比較簡單一點 異常檢測的原理就是假設樣本的個特徵值都呈高斯分佈，選擇分佈較離散的樣本的作為異常值。這裡主要注意的是通過交叉驗證對閾值的選擇和F1score的應用。 原始資料：

吳恩達-機器學習(9)-異常檢測、協同過濾

文章目錄 Density Estimation Problem Motivation Gaussian Distribution Algorithm Building an Anomaly

機器學習筆記——異常檢測（anomaly detection）

異常檢測 當我們需要讓一個系統從許多未標註的資料中學習到某些正常的特徵，從而能夠診斷出非正常的資料，我們把這個過程叫做異常檢測 我們要做的就是對於給定的一組特徵值，我們輸出一個概率，如果這個概率值小於某個臨界值，代表資料異常 演算法 我們可以採用高斯函式來擬合這個概率值，

斯坦福大學機器學習筆記——異常檢測演算法（高斯分佈、多元高斯分佈、異常檢測演算法）

異常檢測問題介紹： 異常檢測演算法主要用於無監督學習問題，但從某種角度看它又類似於一種有監督學習的問題，下面我們從一個例子中簡單介紹一下什麼是異常檢測問題。 比如我們有一個飛機引擎製造商，對於一個新造出的飛機引擎我們想判斷這個引擎是不是異常的。 假如我們有

【機器學習】異常點檢測_sklearn

注意Novelty和Outlier的區別 novelty detection:   The training data is not polluted by outliers, and we are interested in det

pandas學習(常用數學統計方法總結、讀取或保存數據、缺省值和異常值處理)

導入 numpy shape 缺省 數量 導入數據 個數 就是 msu pandas學習(常用數學統計方法總結、讀取或保存數據、缺省值和異常值處理) 目錄 常用數學統計方法總結 讀取或保存數據 缺省值和異常值處理 　　 常用數學統計方法總結 count

吳恩達機器學習：異常檢測與協同過濾

這是吳恩達機器學習的最後一課，這次學習的內容是機器學習的常見應用，異常檢測與協同過濾。課程中介紹的異常檢測主要基於 正態分佈，用於檢測出偏離正常值的資料。而協同過濾是 推薦系統 的一部分，利用已有使用者的評分來給你推薦商品、視訊等。 點選 課程視訊 你就能不間

機器學習缺失值處理方法匯總

www. 導致 -m 缺少 噪聲 分析方法 答案 出發點 爆炸 來源網址：http://blog.csdn.net/w352986331qq/article/details/78639233 缺失值處理方法綜述 缺失值是指粗糙數據中由於缺少信息而造成的數據的聚類、分組、刪失

解釋機器學習模型的一些方法（三）——理解復雜的機器學習模型

p s 結果 origin 得出 驗證 場景 這樣的 機器 發的 在這一部分中我們所要展現的技術，可以為非線性、非單調的響應函數生成解釋。我們可以把它們與前兩部分提到的技巧結合起來，增加所有種類模型的可解釋性。實踐者很可能需要使用下列增強解釋性技巧中的一種以上，為他們手中

機器學習中常見優化方法匯總

bsp keep atl 之前 ima http bject ESS ati http://www.scipy-lectures.org/advanced/mathematical_optimization/index.html#a-review-of-the-differ

js檢測資料型別方法總結

1.常用方法typeof var str=‘abc’; console.log(typeof str)//string 2.判斷已知物件型別的方法： instanceof var str='abc'; console.log(str instanceof String);//true

乾貨|機器學習演算法線上部署方法

最近發現了兩個比較好的工具和方法，未來會進行詳細的探索和分析； H2O.AI ,H2O.ai,提供了MOJO和POJO的方式； preditionIO，Welcome to Apache PredictionIO™!，可以基於spark和hbase來提供相應的API服務，還是很方便的

機器學習中的相似性度量總結 [轉]

核函式的含義是兩個輸入變數的相似度，描述相似度的方法有很多種，就本人的專案經驗來說用的最多的是相關係數和歐氏距離。本文對機器學習中常用的相似性度量進行了總結。   作者：蒼梧 連結：https://www.cnblogs.com/heaad/archive/2011/

深度學習最全優化方法總結比較（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）

前言 本文僅對一些常見的優化方法進行直觀介紹和簡單的比較，各種優化方法的詳細內容及公式只好去認真啃論文了，在此我就不贅述了。 SGD 此處的SGD指mini-batch gradient descent，關於batch gradient descent, stochastic gradient de

深度學習中的優化方法總結

梯度下降沿著整個訓練集的梯度方向下降。可以使用隨機梯度下降很大程度地加速，沿著隨機挑選的小批量資料的梯度下降。 批量演算法和小批量演算法 使用小批量的原因 n個樣本均值的標準差是σn√σn，其中σσ是樣本值真實的標準差。分母n−−√n表明使用更多的樣本來估計梯度的方

2018最新實用BAT機器學習演算法崗位系列面試總結(結構化資料特徵工程)

特徵工程，是對原始資料進行一系列工程處理，目的是去除原始資料中的雜質和冗餘，設計更高效的特徵來描述求解的問題與預測模型之間的關係。 特徵工程主要對以下兩種常用的資料型別做處理： （1）結構化資料。結構化資料型別可以看作關係型資料庫的一張表，每列都有清晰的定義，包