凸包（Convex Hull）

在圖形學中，凸包是一個非常重要的概念。簡明的說，在平面中給出N個點，找出一個由其中某些點作為頂點組成的凸多邊形，恰好能圍住所有的N個點。

這十分像是在一塊木板上釘了N個釘子，然後用一根繃緊的橡皮筋它們都圈起來，這根橡皮筋的形狀就是所謂的凸包。

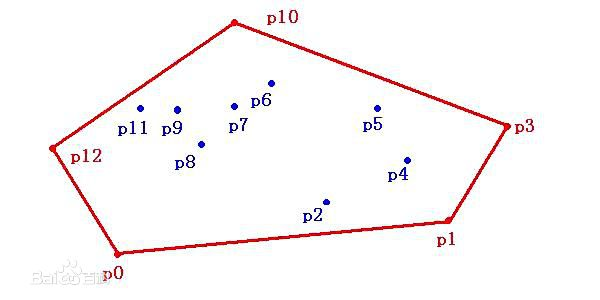
計算凸包的一個著名演算法是Graham Scan法，它的時間複雜度與所採用的排序演算法時間複雜度相同，通常採用線性對數演算法，因此為\( O\left(N\mathrm{log}\left(N\right)\right) \)。

1. 找到所有點\( P_{0,1,...,N-1} \)中最下方的點，記為\( P_{L} \)；

2. 計算所有其他的點\( P_{i}\left(i\neq L\right) \) 與 \( P_{L} \)構成的向量\( \overrightarrow{P_{L}P_{i}} \)相對於水平軸的夾角。因為所有的點都在該\( P_{L} \)上方，因此向量的取值範圍為\( \left(0, 180\right) \) ，所以可以用餘切值代替角度值；

3. 對所有其他的點按照第2步算出的角度進行排序，且\( P_{L} \)為排序後的陣列的第0位；

4. 從點\( P_{L} \)開始，依此連線每一個點（已經排序過），每連線一個點檢測連線的走向是否是逆時針的，如果是則留下該點的前一個點，反之去除前一個點，使之與前面第二個點直接連線，繼續這一檢測，直到是逆時針或者所有點都被檢測過為止。

判斷三個點依此連成兩條線段走向是否為逆時針，用這兩條線段向量的叉積判斷：叉積>0，逆時針；反之順時針或者共線。

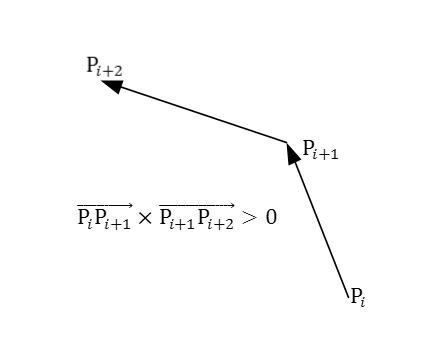
這裡採用Qt 5.7實現了一個演算法的演示程式，其中演算法的部分如下（由於在Qt的座標系中，y向下增長，因此在計算縱座標差值時需要取相反數）。

void DisplayWidget::calConvexHull()
{
    int size = m_points.size();
    if (size < 3)
    {
        return;
    }

    // First: find the lowest point
 

    int maxY = 0;
    int indexOfLowest = -1;
    for (int i = 0; i < size; i++)
    {
        if (m_points.at(i).y() > maxY)
        {
            maxY = m_points.at(i).y();
            indexOfLowest = i;
        }
    }

    std::swap(*m_points.begin(), *(m_points.begin() + indexOfLowest));
    QPoint &lowestPoint = *(m_points.begin());


    // Second: calculate ctan(angles)
    double *ctanAngles = new double[size];
    for (int i = 1; i < size; i++)
    {
        double deltaY = lowestPoint.y() - m_points.at(i).y() + DBL_EPSILON;
        double deltaX = m_points.at(i).x() - lowestPoint.x();
        ctanAngles[i] = deltaX / deltaY;
    }

    // Third: Sort subscript
    int *subscript = new int[size];
    for (int i = 1; i < size; i++)
    {
        subscript[i] = i;
    }
    std::sort(subscript + 1, subscript + size, [ctanAngles](int a1, int a2) { return ctanAngles[a2] < ctanAngles[a1]; });

    // Fourth: Calculate convex hull
    std::vector<QPoint> convexHullPoints;
    convexHullPoints.push_back(*m_points.begin());
    convexHullPoints.push_back(m_points.at(subscript[1]));

    for (int i = 2; i < size; i++)
    {
        convexHullPoints.push_back(m_points.at(subscript[i]));
        while (convexHullPoints.size() > 3 && 
               !isAnticlockwise(*(convexHullPoints.end() - 3), *(convexHullPoints.end() - 2), *(convexHullPoints.end() - 1)))
        {
            *(convexHullPoints.end() - 2) = *(convexHullPoints.end() - 1);
            convexHullPoints.pop_back();
        } 
    }

    m_convexHullPoints = std::move(convexHullPoints);

    delete[] ctanAngles;
    delete[] subscript;
}

效果如下：

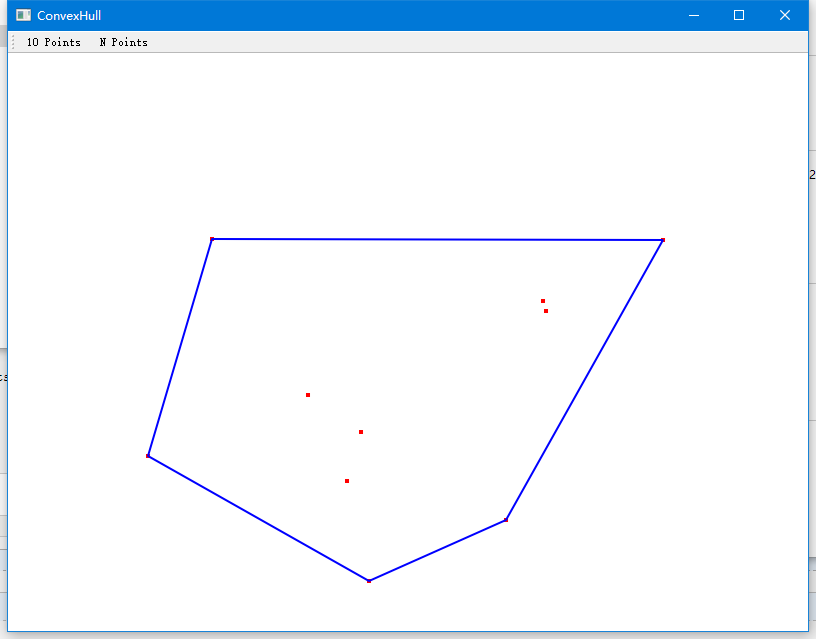
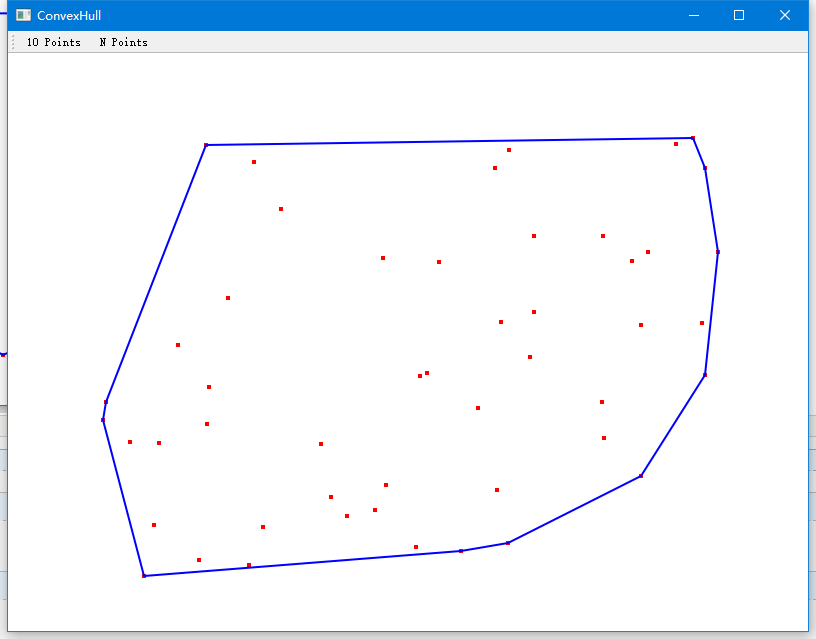
程式原始碼：http://files.cnblogs.com/files/HolyChen/ConvexHull.rar