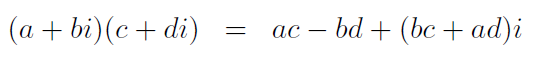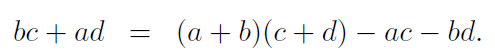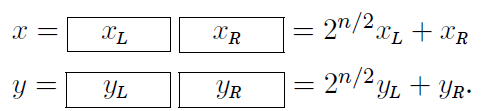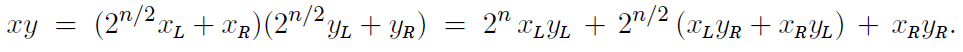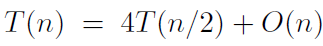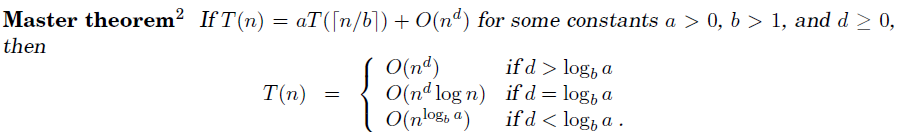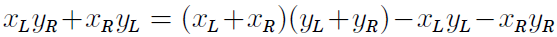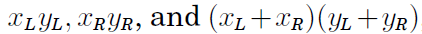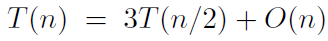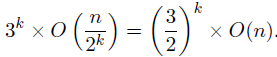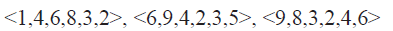演算法課筆記系列(一)—— 分治演算法
首先必須強調的是,我是個演算法渣,多少年了~~還是渣/(ㄒoㄒ)/~~
這學期在上英文演算法課,機緣巧合選了英文,覺得老師講得還不錯,所以沒換到中文。想要通過這樣總結一下加深演算法理解,考試時也方便複習。
第一次課是對學習演算法課需要的數學基礎知識的複習,如集合以及集合的操作,函式,關係等,和一些數學證明方法的介紹,包括通過構造證明,通過對照證明(舉反例,找矛盾),通過案例證明(可以理解為分情況討論證明同一個結論對任一情況都成立),通過數學歸納法證明(包含最小反例法則,數學歸納的強法則)。
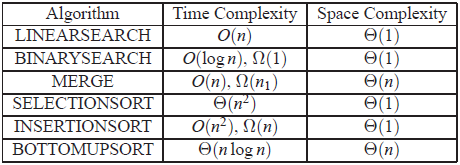
第二次課是接觸演算法必須的演算法複雜度分析,包括時間和空間上的複雜度分析。通過列舉了幾個演算法實際案例進行的分析,包括兩種搜尋方法(線性搜尋,二分搜尋),一個合併演算法(將兩個已經排好序的列表合併)和三種排序演算法(選擇排序,插入排序和合並排序)。
第一個詳細講的演算法是分治演算法,該演算法主要用於解決這樣條件下的問題:
(1) 可以被分解成若干個相同的更小的子問題,即該問題具有最優子結構性質;分解到一定的程度就會很容易解決;
(2) 可以迴圈解決這些子問題;
(3) 最後可以合適的將子問題的解合併為該問題的解;
(4) 該問題分解出的各個子問題是相互獨立的,即子問題之間不包含公共的子問題
實際問題就是逐一地解決這三個步驟:在將問題分解成子問題;在遞迴的最後一步,當問題變得足夠小的時候,可以被直接解決了;以及將子問題的答案合併。
使用分治演算法的經典例子如下:
(一) 乘法運算
(二) Merge排序
(三) 求中位數
(四) 矩陣的乘法
先就乘法操作進行一下推導。
(一) 乘法操作
該演算法是根據高斯的一個發現,將兩個複數的乘法
原本的四個乘法操作現在將其轉化為三個,
簡單看來,認為減少的複雜度並不多。但是當應用到迭代中,會發現可以大大減小複雜度。
對這個的證明可以將其從複數一般化到整型的乘法。假設x和y是兩個n位的整數,為了方便假設n都是2的冪。由以上條件,我們可以將x和y轉化為如下形式:
這樣一來,x和y的乘積可以表示為:
通過轉化後的式子來計算xy,加法操作和這裡的2的冪都是線性的複雜度,因為對2求冪就是一個左移的位操作。現在,乘法操作就變成了對四個n/2位的數進行乘法操作的迭代(子問題是原來大小的一半),然後在O(n)時間內將之前的結果進行整合。這樣,使用master theorem來計算整個過程的複雜度的話就是
計算得到演算法的複雜度為O(n^2).
(備註:master theorem如下:
為了提升演算法的執行效率,只用之前高斯提到的方法。原來的四個乘法操作可以轉化為三個,
即
這樣的話,使用master theorem來計算整個過程的複雜度的話就是
,在每一次迭代中,常量從4變為3,計算出來複雜度為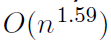
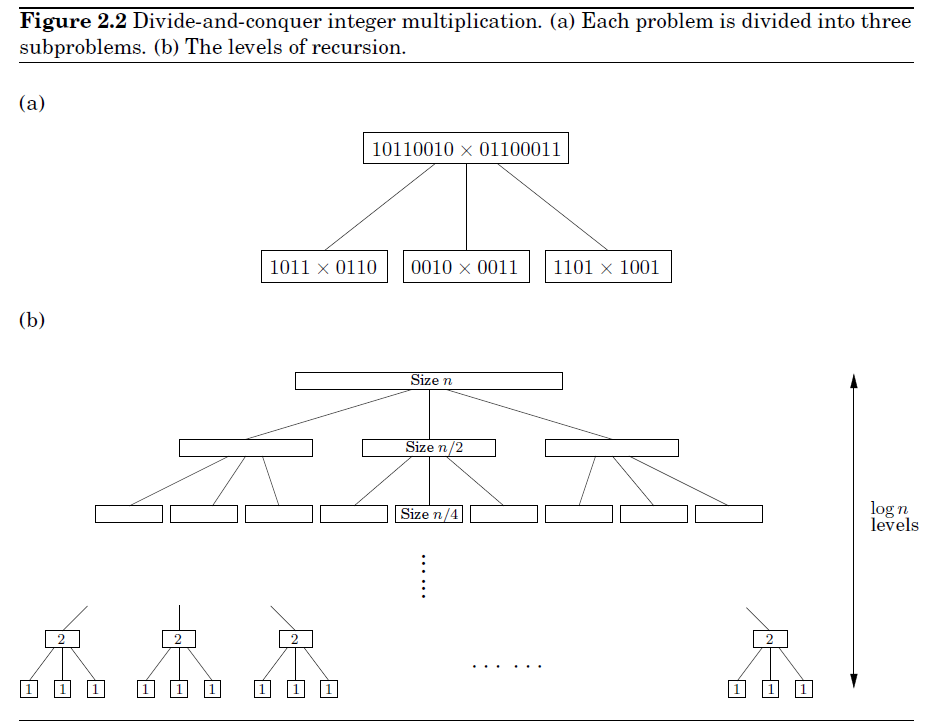
該問題的迭代過程可以通過一棵樹來描述。
在子問題的每一次迭代中,問題的規模就減小一半。在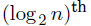

在樹的最高層,k=0,則複雜度為O(n)。在最底層,k=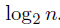
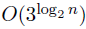
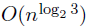

使用之前的思路,則這棵迭代數的分支因子為4,則計算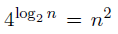
因此,在分治演算法中,子問題的數目可以被解釋為迭代樹的分支因子(master theorem中的a),每一次問題規模的變化係數為b(減小一半就是1/2),最後將子問題的所有解合併起來的複雜度中n的冪指數即為d。
例如,二分查詢中,在一個已經排好序的序列z[0,1,…,n-1]中找到數k,首先將k與z[2/n]進行比較,根據結果在決定是在前半部分繼續比較還是後半部分繼續比較。這樣得到的迭代公式為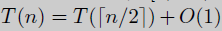

最後一部分講了關於Sorting Network的畫法,上課的時候聽得比較模糊。下來整理一下之後,過程如下:
1)首先建立一個Bitonic Sorter
先說Bitonic sequence,中文翻譯為雙調序列,也就是單調遞增和單調遞減的的序列,也可以迴圈轉換先單調遞增再單調遞減。
例如:
Half-cleaner是長度為1的比較網路,是第i個輸入與第i+n/2個輸入比較(假設n是偶數,i = 1,2,...n/2)
如下圖:
這樣得到的雙調序列上半部分是更小的值,下半部分是更大的值。上下兩部分都是雙調的。
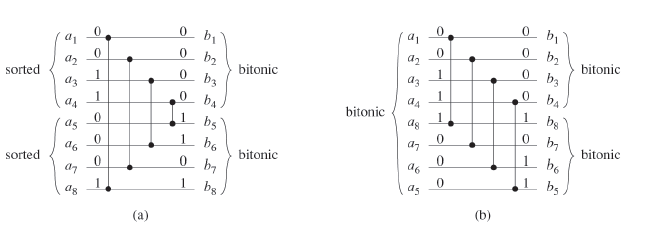
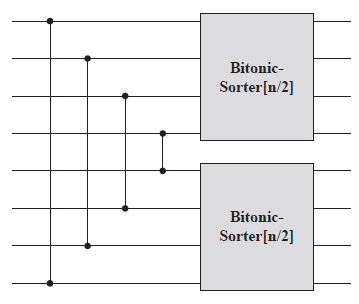
然後就可以畫Bitonic Sorter的結構:
下面右圖為n = 8時的Bitonic Sorter

2)第二步構造一個Merger
Merger與Half-cleaner是有區別的,Merger[n]是將兩個單調的輸入序列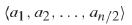
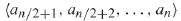


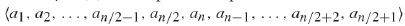
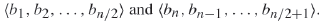
於是構建的Merger如下:
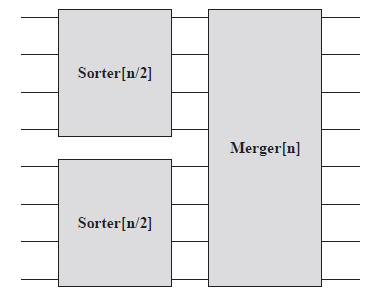
3)最後一步就是構造Sorter
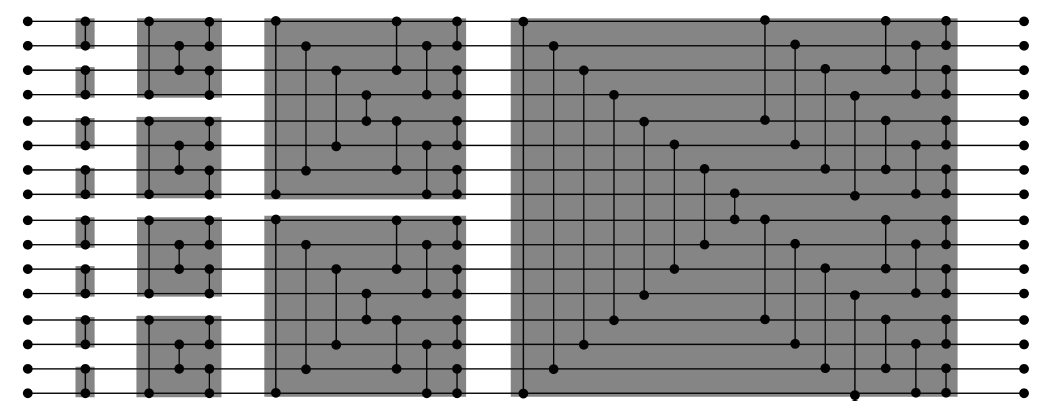
下面給出n=8和n=16時的sorting network:
n = 8:
n = 16:
相關推薦
演算法課筆記系列(一)—— 分治演算法
首先必須強調的是,我是個演算法渣,多少年了~~還是渣/(ㄒoㄒ)/~~ 這學期在上英文演算法課,機緣巧合選了英文,覺得老師講得還不錯,所以沒換到中文。想要通過這樣總結一下加深演算法理解,考試時也方便複
人工智慧筆記系列(一)
參考資料:《人工智慧:一種現代的方法》 持續完善中。。。 人工智慧的定義 兩個維度 外部表現:思考、行動 評判:像人一樣、合理性 通過兩個維度的交叉形成4種定義方法 像人一樣思考——認知科學 像人一樣行動——圖靈測試 合理地思
資料結構和演算法躬行記(7)——分治演算法
分治演算法(Divide-and-Conquer Algorithm),就是分而治之,把一個複雜問題分成兩個或更多個相同或相似的子問題,直到最後子問題可以簡單的直接求解,原問題的解即子問題的解的合併。 分治演算法比較適合用遞迴來實現,而每一層遞迴都會涉及三個操作: (1)分解:將原問題分解為若干個
死磕java concurrent包系列(一)從樂觀鎖、悲觀鎖到AtomicInteger的CAS演算法
前言 Java中有各式各樣的鎖,主流的鎖和概念如下: 這篇文章主要是為了讓大家通過樂觀鎖和悲觀鎖出發,理解CAS演算法,因為CAS是整個Concurrent包的基礎。 樂觀鎖和悲觀鎖 首先,java和資料庫中都有這種概念,他是一種從執行緒同步的角度上看的一種廣義上的概念: 悲觀鎖:悲觀的認為自己在使用資料的
STM32開發筆記47:STM32F4+DP83848乙太網通訊指南系列(一):知識儲備
微控制器型號:STM32F407VGT 本章為系列指南第一章,主要是介紹一下專案思路,並且儘可能列出從零開始著手開發這個專案過程中,所需要理解的各類知識點,關於這些知識點,如果需要更詳細的介紹,請列為看官自行百度谷歌。 STM32F407簡介 STM32F407主頻168MHz,主頻
機器學習技法筆記總結(一)SVM系列總結及實戰
機器學技法筆記總結(一)SVM系列總結及實戰 1、原理總結 在機器學習課程的第1-6課,主要學習了SVM支援向量機。 SVM是一種二類分類模型。它的基本模型是在特徵空間中尋找間隔最大化的分離超平面的線性分類器。 (1)當訓練樣本線性可分時,通過硬間隔最大化,學習
演算法設計與分析(一)——遞迴與分治
目錄 D、走迷宮 提示: 提示: NOJ 2018.9.21 A、二分查詢 時限:1000ms 記憶體限制:10000K 總時限:3000ms 描述 給定一個單調遞增的整數序列,問某個整數是否在序列中。 輸入
迴歸演算法(python code)----------機器學習系列(一)
前面一篇把迴歸演算法的理論部分都大致講過了,這一篇主要就python程式碼部分做一些解釋,也就是怎麼用python寫回歸演算法,因為LZ也是剛剛入門,有一些理解不對的地方,歡迎大家指正,LZ也矯枉過正。 首先是python模組----numpy (設計用到的數學
演算法快學筆記(一):演算法入門
1. 演算法的定義 “演算法”一詞在不同的書籍以及網站上可能會存在一些差異,但是下面的定義個人覺得最為貼切: 1. 演算法代表著用系統的方法描述解決問題的策略機制 2. 能夠對一定規範的輸入,在有限時間內獲得所要求的輸出 3. 一個演算法的優劣可以用空間複雜度與時間複雜度來衡量
演算法學習(一)——分治以及排序演算法總結
分治策略: 分解(Divide):將問題劃分為若干子問題 解決(Conquer):遞迴求解子問題 合併(combine):子問題組合成原問題 主方法:T(n) = aT(n/b)+f(n) 分解成a個問題,每個子問題降b倍,合併為O(f(n)) 主定理: 比
Memcache(MC)系列(一)Memcache介紹、使用、儲存、演算法、優化
寫在前面:前不久在工作中被問到關於MC一致雜湊的問題,由於時隔太久幾乎忘記,特前來惡補一下MC,以下是前幾年在工作中學習MC時的一些資料,來歷不明,特整理一下,希望對大家的學習也能有所幫助。1、memcached 介紹1.1 memcached 是什麼?memcached 是
讀書筆記_演算法第四版(一)
演算法第四版(謝路雲譯) 第1章 基礎 1.1 基礎程式設計模型 l Java程式的基本結構;原始資料型別與表示式;語句;簡便記法;陣列;靜態方法;API;字串;輸入輸出;二分查詢。 l 以下為“答疑”和“練習”中的知識點: l Math.abs(-2147483
浙大人工智慧演算法與系統課程作業指南系列(一)口罩識別的資料處理部分
# 浙大人工智慧演算法與系統課程作業指南系列(一)口罩識別的資料處理部分 寫在前面: 我原來本科的時候並不是計算機專業的,屬於跨考到計算機這個專業的。在本科期間也就接觸了點C的基礎,然後因為是傳統工科,所以Matlab和Fortran也寫過一些程式碼,趁著考完研的暑假繼續學習了一下C++,順便拿B站上能搜
【ABAP自學系列(一)】
發的 img api .cn ima code pat 查看 屏幕 一、查看補丁包級別 然後看Patch Level即可。 常用T-code: SE38(寫程序) SE80(屏幕開發) Smartform(開發smartform打印) SE37(可以查看function
Linux基礎學習系列(一)
內核版本 比較 其中 問題 測試版 工具 含義 語言 復制 Linux是一種類似於UNIX的操作系統,由Linus Torvalds於1991年在minix操作系統的基礎創建。Linux憑借其優良特性已經成為目前發展潛力最大的操作系統。 Linux的版本有內核版本和
spring boot學習系列(一)
web服務器 應用程序 spring 控制器 做什麽 spring boot開發第一個應用程序1、spring boot是什麽?2、spring boot容易上手嗎?寫這篇文章技術文章,主要是記錄日常的學習以及理解。我們重新認識一下spring假設你受命使用spring開發一個簡單的hel
asp.net core入門教程系列 (一)
home padding 方式 title sys 活性 elf tro ash Asp.Net Core簡介 ASP.NET Core 是一個全新的開源、跨平臺框架,可以用它來構建基於網絡連接的現代雲應用程序,比如:Web 應用,IoT(Internet Of Thin
【原創】源碼角度分析Android的消息機制系列(一)——Android消息機制概述
run 權限 開發 等待 通過 讀取 概述 走了 color ι 版權聲明:本文為博主原創文章,未經博主允許不得轉載。 1.為什麽需要Android的消息機制 因為Android系統不允許在子線程中去訪問UI,即Android系統不允許在子線程中更新UI。 為什麽不允許
vue系列(一)子組件和父組件
top parent sage too msg pro 工具 light java 父組件傳遞數據到子組件props 父組件 <template> <div class="main"> <div class="top">
Hadoop源碼系列(一)FairScheduler申請和分配container的過程
opened running fetch utils ostream png on() threshold metadata 1、如何申請資源 1.1 如何啟動AM並申請資源 1.1.1 如何啟動AM val yarnClient = YarnClient.createY