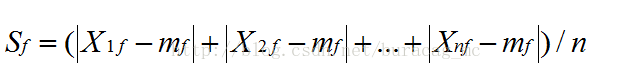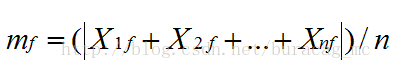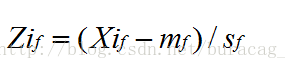聚類演算法(基礎及核心概念)
聚類分析簡介
將物理或抽象物件的集合分組成為由類似的物件組成的多個類的過程被稱為聚類。由聚類所生成的簇是一組資料物件的集合,這些物件與同一個簇中的物件彼此相似,與其他簇中的物件相異。在許多應用中,一個簇中的資料物件可以被作為一個整體來對待。
作為統計學的一個分支,聚類分析已經被廣泛地研究了許多年。基於k-means(統計學教材聚類分析部分必講),k-medoids和其他一些方法的聚類分析工具已經被加入到許多統計分析軟體包或系統中,例如典型的SPSS和SAS。在機器學習領域,聚類是無監督學習(unsupervised learning)的一個典型例子。在概念聚類(conceptual clustering
相異度是基於描述物件的屬性值來計算的。距離和相關性是經常採用的度量方式。其中,衡量距離屬性常見的有歐式距離、曼哈頓(絕對)距離、切比雪夫距離等;衡量相關性常見的有皮爾遜相關係數和斯皮爾曼等級相關係數。
聚類分析中的資料型別
1.先介紹一下在聚類中具有代表性的兩種資料結構:
資料矩陣(Data matrix,或稱為物件屬性結構):它用p個變數(也稱為屬性)來表現n個物件, 例如用年齡,身高,性別,種族等屬性來表現物件“人”。這種資料結構是關係表的形式,或 者看為
相異度矩陣(dissimilarity matrix,或稱為物件-物件結構):儲存n個物件兩兩之間的近似性, 表現形式是一個n*n維的矩陣。
2.資料標準化
為了實現度量值的標準化,一種方法是將原來的度量值轉換為無單位的值(即統計學中所說的無量綱化)。給定一個變數f的度量值,可以進行如下的變換:
## 計算平均的絕對偏差(mean absolute deviation):
這裡的 x1f,…,xnf是f的n個度量值,mf是f的平均值,即:
## 計算標準化的度量值,即z-score:
3.資料標準化後,就是計算物件之間的相異度
## 以距離作為度量:
另外,當q=無窮時,稱作切比雪夫距離。
## 以相似性作為度量,同樣,我們為了簡單說明,我就直接擷取前面博文的圖如下:
這裡,再補充一下如何用二元變數描述物件間的相似度:
一個二元變數只有兩個狀態:0或1,0表示該變數為空,1表示該變數存在。例如,給出一個描述病人的變數smoker,1表示病人抽菸,而0表示病人不抽菸。如果用標準化的方法處理會誤導聚類結果,所以要採用特定的方法來計算其相異度。
如果假設所有的二元變數有相同的權重,我們設q是物件i和j值都為1的變數的數目,r是在物件i中值為1,在物件j中值為0的變數的數目,s是在物件i中值0,在物件j中值為1的變數的數目,t是在物件i和j中值都0的變數的數目。變數的總數是p,p=q+r+s+t。
| j為1 | j為0 | |
| i為1 | q | r |
| i為0 | s | t |
基於對稱二元變數的相似度稱為恆定的相似度,即當一些或者全部二元變數編碼改變時,計算結果不會發生變化。對恆定的相似度來說,評價兩個物件i和j之間相異度的著名的係數是簡單匹配係數,其定義如下:
D(i,j) = (r+s) / (q+r+s+t)
而對非恆定的相似度,著名的評價係數是Jaccard係數,在它的計算中,負匹配的數目被認為是不重要的,因此被忽略,其定義如下:
D(i,j) = (r+s) / (q+r+s)
主要聚類分析方法的分類
劃分方法
劃分方法(partitioning methods):給定一個n個物件或元組的資料庫,一個劃分方法構建資料的k個劃分,每個劃分表示一個聚類,並且k<=n。也就是說,它將資料劃分為k個組,同時滿足如下的要求:
1.每個組至少包含一個物件;
2.每個物件必須屬於且只屬於一個組。注意在某些模糊劃分技術中第二個要求可以放寬。
給定k,即要構建的劃分的數目,劃分方法首先建立一個初始劃分。然後採用一種迭代的重定位技術,嘗試通過物件在劃分間移動來改進劃分。一個好的劃分的一般準則是:在同一個類中的物件之間的距離儘可能小,而不同類中的物件之間的距離儘可能大。
為了達到全域性優,基於劃分的聚類會要求窮舉所有可能的劃分。實際上,絕大多數應用採用 了以下兩個比較流行的啟發式方法:
1.k-means 演算法,在該演算法中,每個簇用該簇中物件的平均值來表示。
2.k-medoids 演算法,在該演算法中,每個簇用接近聚類中心的一個物件來表示。
這些啟發式聚類方法對在中小規模的資料庫中發現球狀簇很適用。
層次方法
層次的方法(hierarchical methods):層次的方法對給定資料集合進行層次的分解。根據層次的分解如何形成,層次的方法可以被分為凝聚的或分裂的方法。
凝聚的方法,也稱為自底向上的方法,一開始將每個物件作為單獨的一個組,然後繼續地合併相近的物件或組,直到所有的組合併為一個(層次的上層),或者達到一個終止條件。
分裂的方法,也稱為自頂向下的方法,一開始將所有的物件置於一個簇中。在迭代的每一步中,一個簇被分裂為更小的簇,直到終每個物件在單獨的一個簇中,或者達到一個終止條件。
基於密度的方法
基於密度的方法:絕大多數劃分方法基於物件之間的距離進行聚類。這樣的方法只能發現球狀的簇,而在發現任意形狀的簇上遇到了困難。隨之提出了基於密度的另一類聚類方法,其主要思想是:只要臨近區域的密度(物件或資料點的數目)超過某個閾值,就繼續聚類。也就是說,對給定類中的每個資料點,在一個給定範圍的區域中必須包含至少某個數目的點。這樣的方法可以用來過濾“噪音”資料,發現任意形狀的簇。
DBSCAN是一個有代表性的基於密度的方法,它根據一個密度閾值來控制簇的增長。OPTICS是另一個基於密度的方法,它為自動的,互動的聚類分析計算一個聚類順序
除此之外,還有基於網格的方法和基於模型的方法。
本文大概梳理了一下聚類分析的基礎概念以及各分類方法的思想,隨後會將具體的演算法實現寫上。
相關推薦
聚類演算法(基礎及核心概念)
聚類分析簡介 將物理或抽象物件的集合分組成為由類似的物件組成的多個類的過程被稱為聚類。由聚類所生成的簇是一組資料物件的集合,這些物件與同一個簇中的物件彼此相似,與其他簇中的物件相異。在許多應用中,一個簇中的資料物件可以被作為一個整體來對待。 作為統計學的一個分支,聚類分
聚類演算法(三)——基於密度的聚類演算法(以 DBSCAN 為例)
上一篇部落格提到 K-kmeans 演算法存在好幾個缺陷,其中之一就是該演算法無法聚類哪些非凸的資料集,也就是說,K-means 聚類的形狀一般只能是球狀的,不能推廣到任意的形狀。本文介紹一種基於密度的聚類方法,可以聚類任意的形狀。 基於密度的聚類是
鳶尾花三種聚類演算法(K-means,AGNES,DBScan)的python實現
一.分散性聚類(kmeans) 演算法流程: 1.選擇聚類的個數k. 2.任意產生k個聚類,然後確定聚類中心,或者直接生成k箇中心。 3.對每個點確定其聚類中心點。 4.再計算其聚類新中心。 5.重複以上步驟直到滿足收斂要求。(通常就是確定的中心點不再改變。
機器學習總結(十):常用聚類演算法(Kmeans、密度聚類、層次聚類)及常見問題
任務:將資料集中的樣本劃分成若干個通常不相交的子集。 效能度量:類內相似度高,類間相似度低。兩大類:1.有參考標籤,外部指標;2.無參照,內部指標。 距離計算:非負性,同一性(與自身距離為0),對稱性
LR演算法(基礎及核心概念)
前言 首先需要清楚的是,LR(Logistic Regression)雖然是迴歸模型,但卻是經典的分類方法。 為什麼分類不用SVM呢?我們對比一下SVM,在二分類問題中,如果你問SVM,它只會回答你該樣本是正類還是負類;而你如果問LR,它則會回答你該樣本是正類
EM演算法(基礎及核心概念)
Jensen不等式 其實在運籌學以及基礎的優化理論中,便有涉及。設f是定義域為實數的函式,如果對於所有的實數x,,那麼f是凸函式。拓展到多元的情形,x是向量時,如果其對應的Hessian矩陣H是半正定的(),那麼f是凸函式。特別的,當或者海瑟矩陣為正定時(H&
聚類演算法(1)
一聚類演算法簡介 1.聚類和分類的區別 聚類 - 利用演算法將相似或者相近的樣本聚成一簇,這些樣本都是無標籤的,是一種無監督學習演算法。 分類 - 首先需要從有標籤樣本學習出打標籤邏輯,再利用學習出的邏輯對無標籤樣本進行分類,是一種有監督學習演算法。 2.聚類的使用 聚類演
機器學習實戰(Machine Learning in Action)學習筆記————06.k-均值聚類演算法(kMeans)學習筆記
機器學習實戰(Machine Learning in Action)學習筆記————06.k-均值聚類演算法(kMeans)學習筆記關鍵字:k-均值、kMeans、聚類、非監督學習作者:米倉山下時間:2018-11-3機器學習實戰(Machine Learning in Action,@author: Pet
吳恩達老師機器學習筆記K-means聚類演算法(二)
運用K-means聚類演算法進行影象壓縮 趁熱打鐵,修改之前的演算法來做第二個練習—影象壓縮 原始圖片如下: 程式碼如下: X =imread('bird.png'); % 讀取圖片 X =im2double(X); % unit8轉成double型別 [m,n,z]=size
吳恩達老師機器學習筆記K-means聚類演算法(一)
今天接著學習聚類演算法 以後堅決要八點之前起床學習!不要浪費每一個早晨。 K-means聚類演算法聚類過程如下: 原理基本就是先從樣本中隨機選擇聚類中心,計算樣本到聚類中心的距離,選擇樣本最近的中心作為該樣本的類別。最後某一類樣本的座標平均值作為新聚類中心的座標,如此往復。 原
聚類演算法(二)
密度聚類 密度聚類假設聚類結構能通過樣本分佈的緊密程度確定,通常情況下密度聚類演算法從樣本密度的角度來考察樣本之間的可連線性,並基於可連線樣本不斷擴充套件聚類 簇以獲得最終的聚類結果 DBSCAN 基於一組鄰域引數來刻畫樣本分佈的緊密程度。 事先不用預設聚類簇數
大資料聚類演算法效能比較及實驗報告
在大資料領域這個聚類演算法真是起到了十分重要的作用,只有通過有效地聚類才能得到非常直觀的結果。 有一個實驗要求對比兩種大資料聚類演算法的效能,具體的程式碼也不是由我實現的,我只是改了一部分,主要還是部落格大佬們的程式碼,我這裡借用了一下~~ 具體的實驗報告和
聚類演算法(一)—— k-means演算法以及其改進演算法
聚類演算法是一種無監督學習,它把資料分成若干類,同一類中的資料的相似性應儘可能地大,不同類中的資料的差異性應儘可能地大。聚類演算法可分為“軟聚類”和“硬聚類”,對於“硬聚類”,樣本中的每一個點都是 100%確定分到某一個類別;而“軟聚類”是指樣本點以一定的概率被分
層次聚類演算法的原理及python實現
層次聚類(Hierarchical Clustering)是一種聚類演算法,通過計算不同類別資料點間的相似度來建立一棵有層次的巢狀聚類樹。在聚類樹中,不同類別的原始資料點是樹的最低層,樹的頂層是一個聚類的根節點。 聚類樹的建立方法:自下而上的合併,自上而下的分裂。(這裡介紹第一種) 1.2 層次聚類的合
使用Matlab完成層次聚類演算法(最小生成樹演算法)
最近要寫作業,涉及到一些聚類演算法。 關於聚類演算法的一些理論和定義,請參照部落格http://blog.sina.com.cn/s/blog_62f3c4ef01014uhe.html 和大傳送術http://blog.csdn.net/a1b2c3d4123456/a
K-means和PAM聚類演算法Python實現及對比
K-means(K均值劃分)聚類:簡單的說,一般流程如下:先隨機選取k個點,將每個點分配給它們,得到最初的k個分類;在每個分類中計算均值,將點重新分配,劃歸到最近的中心點;重複上述步驟直到點的劃歸不再改變。下圖是K-means方法的示意。 PAM
MATLAB學習之路(一) 實現簡單的基於歐式距離的新型聚類演算法(Clustering by fast search and find of density peaksd)
大學本科三年,眨眼而已,對於一個考研黨來說,本科時間已所剩不多,大三上學期初次接觸到MATLAB。的確如大牛們所說,強大的計算能力,充足的數學工具,帶來使用者極大的便利。 在大資料的學習過程中,MAT
聚類演算法(二)、聚類演算法的系統性比較
聚類是試圖將資料集中的樣本劃分為若干個不相交的子集。每個子集稱為一個“簇”(cluster)。聚類既能作為一個單獨的過程,也可以作為分類等其他學習任務的前驅任務、例如,在一些商業應用中,需要對新使用者的型別進行判別,但是定義“使用者l型別”對商家來說可不容易,此時
K-Means聚類演算法的原理及實現
問題導讀: 1、如何理解K-Means演算法? 2、如何尋找K值及初始質心? 3、如何應用K-Means演算法處理資料?K-Means是聚類演算法中的一種,其中K表示類別數,Means表示均值。顧名思義K-Means是一種通過均值對資料點進行聚類的演算法。K-Means演算
常用聚類演算法(一) DBSCAN演算法
1、DBSCAN簡介 DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪聲的基於密度的聚類方法)是一種基於密度的空間聚類演算法。該演算法將具有足夠密度的區域劃分為簇,並在具有噪聲的