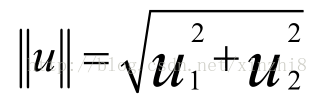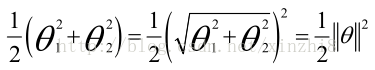在本篇博文中，我將介紹一些大邊界分類背後的數學原理。你將對支援向量機中的優化問題，以及如何得到大邊界分類器，產生更好的直觀理解。

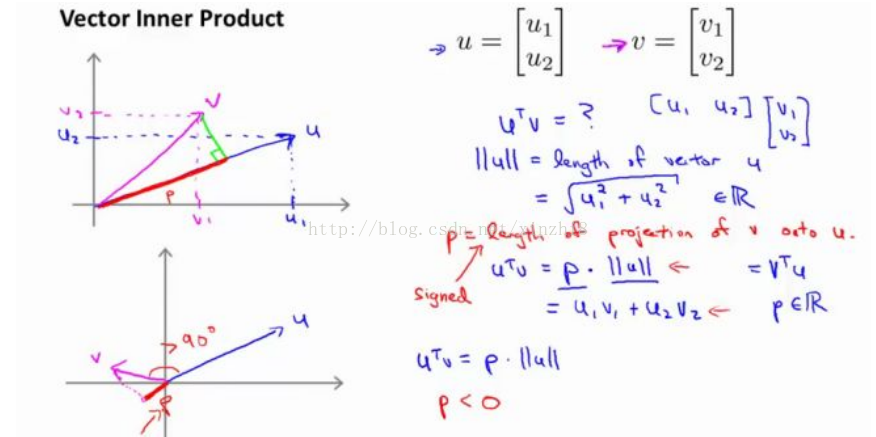
    首先，讓我來給大家複習一下關於向量內積的知識。假設我有兩個向量，u 和 v 我將它們寫在這裡。兩個都是二維向量，我們看一下，uT v 的結果。u T v 也叫做向量 u 和 v 之間的內積。由於是二維向量，我可以將它們畫在這個座標系上。我們說，這就是向量 u 即在橫軸上，取值為某個 u 1 ，而在縱軸上，高度是某個 u 2 作為 u 的第二個分量。現在，很容易計算的一個量就是向量 u 的範數。||u|| 表示 u 的範數，即 u 的長度，即向量 u 的歐幾里得長度。根據畢達哥拉斯定理：

這是向量 u 的長度，它是一個實數。現在你知道了這個的長度是多少了。我剛剛畫的這個向量的長度就知道了。現在讓我們回頭來看向量 v ，因為我們想計算 內積。v 是另一個向量，它的兩個分量 v 1 和 v 2 是已知的。向量 v 可以畫在這裡，現在讓我們來看看如何計算 u 和 v 之間的內積。這就是具體做法，我們將向量 v 投影到向量 u 上，我們做一個直角投影，或者說一個 90 度投影將其投影到 u 上，接下來我度量這條紅線的長度。我稱這條紅線的長度為 p，因此 p 就是長度，或者說是向量 v 投影到向量 u 上的量，我將它寫下來，p 是 v投影到向量 u 上的長度，因此可以將 uT v=p●u ，或者說 u的長度。這是計算內積的一種方法。如果你從幾何上畫出 p 的值，同時畫出 u 的範數，你也會同樣地計算出內積，答案是一樣的。另一個計算公式是：uT v 就是[u1 u2] 這個一行兩列的矩陣乘以 v。因此可以得到 u 1 ×v 1 + u 2 ×v 2 。根據線性代數的知識，這兩個公式會給出同樣的結果。順便說一句，uT v=v T u。因此如果你將 u 和 v 交換位置，將 u 投影到 v 上，而不是將 v投影到 u 上，然後做同樣地計算，只是把 u 和 v 的位置交換一下，你事實上可以得到同樣的結果。申明一點，在這個等式中u 的範數是一個實數，p 也是一個實數，因此 uT v 就是兩個實數正常相乘。

 這就是我們先前給出的支援向量機模型中的目標函式。為了講解方便，我做一點簡化，僅僅是為了讓目標函式更容易被分析。

 我接下來忽略掉截距，令θ 0 = 0，這樣更容易畫示意圖。我將特徵數 n 置為 2，因此我們僅有兩個特徵 x 1 和 x 2 ，現在 我們來看一下目標函式，支援向量機的優化目標函式。當我們僅有兩個特徵，即 n=2 時，這個式子可以寫作：

我們只有兩個引數θ 1 和θ 2 。你可能注意到括號裡面的這一項是向量θ的範數，或者說是向量θ的長度。我的意思是如果我們將向量θ寫出來，那麼我剛剛畫紅線的這一項就是向量θ的長度或範數。這裡我們用的是之前學過的向量範數的定義事實上這就等於向量θ的長度。當然你可以將其寫作θ 0 、θ 1 、θ 2 ，如果θ 0 等於 0，那就是θ 1 θ 2 的長度。在這裡我將忽略θ 0 ，這樣來寫θ的範數，它僅僅和θ 1 θ 2 有關。但是，數學上不管你是否包含θ 0 ，其實並沒有差別，因此在我們接下來的推導中去掉θ 0 不會有影響這意味著我們的目標函式是等於1/2*||θ||^2，因此支援向量機做的全部事情就是 極小化引數向量θ範數的平方或者說長度的平方現在我將要看看這些項：θT X更深入地理解它們的含義。給定引數向量θ給定一個樣本 x，這等於什麼呢? 在前一頁幻燈片上，我們畫出了在不同情形下，uT v 的示意圖，我們將會使用這些概念，θ和 x (i) 就類似於 u 和 v 。

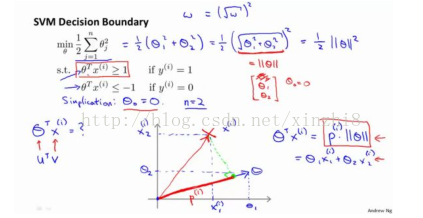
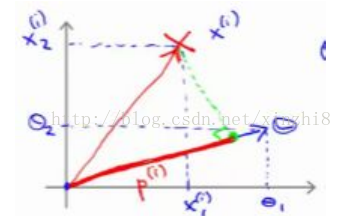
讓我們看一下示意圖：我們考察一個單一的訓練樣本，我有一個正樣本在這裡，用一個叉來表示這個樣本x (i)，意思是在水平軸上取值為x 1(i)，在豎直軸上取值為x2 (i)。這就是我畫出的訓練樣本。儘管我沒有將其真的看做向量。它事實上就是一個始於原點，終點位置在這個訓練樣本點的向量。現在，我們有一個引數向量我會將它也畫成向量。我將θ 1 畫在橫軸這裡，將θ 2 畫在縱軸這裡，那麼內積θ T x (i) 將會是什麼呢？使用我們之前的方法，我們計算的方式就是我將訓練樣本投影到引數向量θ，然後我來看一看這個線段的長度，我將它畫成紅色。我將它稱為 p(i) 用來表示這是第 i 個訓練樣本在引數向量θ上的投影。根據我們之前幻燈片的內容，我們知道的是θ T x (i) 將會等於 p 乘以向量 θ 的長度或範數。這就等於θ1 *x1(i)+θ2*x2 (i)這兩種方式是等價的，都可以用來計算θ和 x (i) 之間的內積。

這告 訴了 我 們 什 麼 呢 ？ 這 裡 表 達 的 意 思 是 ： 

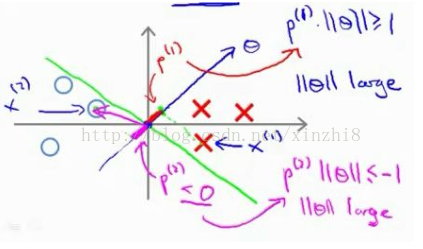
現在讓我們考慮下面這裡的訓練樣本。現在，繼續使用之前的簡化，即θ 0 =0，我們來看一下支援向量機會選擇什麼樣的決策界。這是一種選擇，我們假設支援向量機會選擇這個決策邊界。這不是一個非常好的選擇，因為它的間距很小。這個決策界離訓練樣本的距離很近。我們來看一下為什麼支援向量機不會選擇它。對於這樣選擇的引數θ，可以看到引數向量 θ 事實上是和決策界是 90 度正交的，因此這個綠色的決策界對應著一個引數向量 θ指向這個方向,順便提一句θ 0 =0 的簡化僅僅意味著決策界必須通過原點 (0,0)。現在讓我們看一下這對於優化目標函式意味著什麼。

比如這個樣本，我們假設它是我的第一個樣本 x (1) ，如果我考察這個樣本到引數θ的投影，投影是這個短的紅線段，就等於 p (1) ，它非常短。類似地，這個樣本如果它恰好是 x (2) ， 我的第二個訓練樣本，則它到θ的投影在這裡。我將它畫成粉色，這個短的粉色線段是 p (2) ，即第二個樣本到我的引數向量θ的投影。因此，這個投影非常短。p (2) 事實上是一個負值，p (2) 是在相反的方向，這個向量和引數向量θ的夾角大於 90 度，p (2)的值小於 0。我們會發現這些 p (i) 將會是非常小的數，因此當我們考察優 化 目 標 函 數 的 時 候 ， 對 於 正 樣 本 而 言 ， 我 們 需 要p (i)*||θ||>=1,但是如果 p (i) 在這裡非常小,那就意味著我們需要θ的範數 非 常 大 .因 為如 果 p (1) 很 小,而 我們 希 望p (1)*||θ||>=1,令其實現的唯一的辦法就是這兩個數較大。如果 p (1) 小，我們就希望θ的範數大。類似地，對於負樣本而言我們需要p (2)*||θ||<= -1。我們已經在這個樣本中看到 p (2) 會是一個非常小的數，因此唯一的辦法就是θ的範數變大。但是我們的目標函式是希望找到一個引數θ，它的範數是小的。因此，這看起來不像是一個好的引數向量θ的選擇。

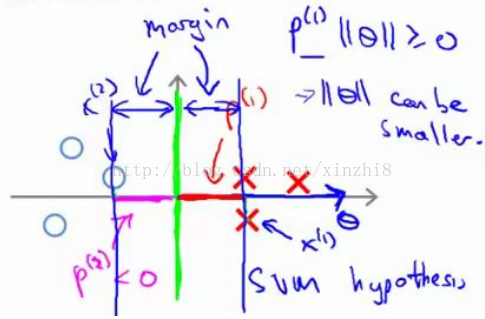
相反的，來看一個不同的決策邊界。比如說，支援向量機選擇了這個決策界，現在狀況會有很大不同。如果這是決策界，這就是相對應的引數θ的方向，因此，在這個決策界之下，垂直線是決策界。使用線性代數的知識，可以說明，這個綠色的決策界有一個垂直於它的向量θ。現在如果你考察你的資料在橫軸 x 上的投影，比如這個我之前提到的樣本，我的樣本 x (1) ，當我將它投影到橫軸 x 上，或說投影到θ上，就會得到這樣的p (1) 。它的長度是 p (1) ，另一個樣本，那個樣本是 x (2) 。我做同樣的投影，我會發現，p (2) 的長度是負值。你會注意到現在 p (1) 和p (2) 這些投影長度是長多了。如果我們仍然要滿足這些約束，p (1)*||θ||>1，則因為 p (1) 變大了，θ 的範數就可以變小了。因此這意味著通過選擇右邊的決策界，而不是左邊的那個，支援向量機可以使引數θ的範數變小很多。因此，如果我們想令θ的範數變小，從而令θ範數的平方變小，就能讓支援向量機選擇右邊的決策界。這就是支援向量機如何能有效地產生大間距分類的原因。看這條綠線，這個綠色的決策界。我們希望正樣本和負樣本投影到θ的值大。要做到這一點的唯一方式就是選擇這條綠線做決策界。這是大間距決策界來區分開正樣本和負樣本這個間距的值。這個間距的值就是 p (1) p (2) p (3) 等等的值。通過讓間距變大，即通過這些 p (1) p (2) p (3) 等等的值，支援向量機最終可以找到一個較小的θ範數。這正是支援向量機中最小化目標函式的目的。