一.概念

支援向量機(Support Vector Machine)，簡稱SVM。是常見的一種判別方法。在機器學習領域，是一個有監督的學習模型，通常用來進行模式識別、分類以及迴歸分析。

SVM的主要思想可以概括為兩點：
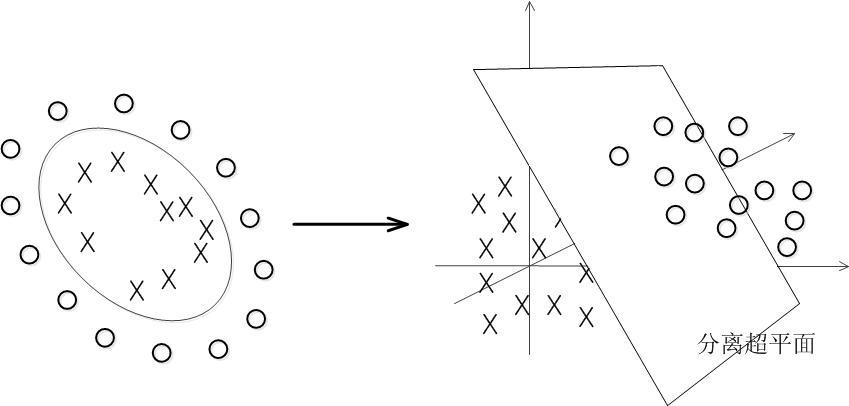
1.它是針對線性可分情況進行分析，對於線性不可分的情況，通過使用非線性對映演算法將低維輸入空間線性不可分的樣本轉化為高維特徵空間使其線性可分，從而使得高維特徵空間採用線性演算法對樣本的非線性特徵進行線性分析成為可能。
2.它基於結構風險最小化理論之上在特徵空間中構建最優超平面，使得學習器得到全域性最優化，並且在整個樣本空間的期望以某個概率滿足一定上界。

二.特徵

⑴SVM學習問題可以表示為凸優化問題，因此可以利用已知的有效演算法發現目標函式的全域性最小值。而其他分類方法（如基於規則的分類器和人工神經網路）都採用一種基於貪心學習的策略來搜尋假設空間，這種方法一般只能獲得區域性最優解。
⑵SVM通過最大化決策邊界的邊緣來控制模型的能力。儘管如此，使用者必須提供其他引數，如使用核函式型別和引入鬆弛變數等。
⑶通過對資料中每個分類屬性引入一個啞變數，SVM可以應用於分類資料。
⑷SVM一般只能用在二類問題，對於多類問題效果不好。

三.分類

3.1線性分類

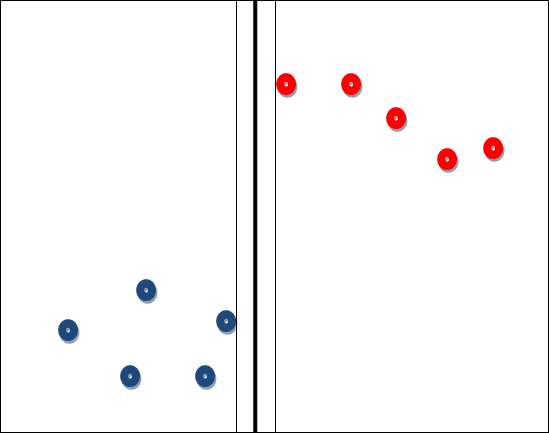
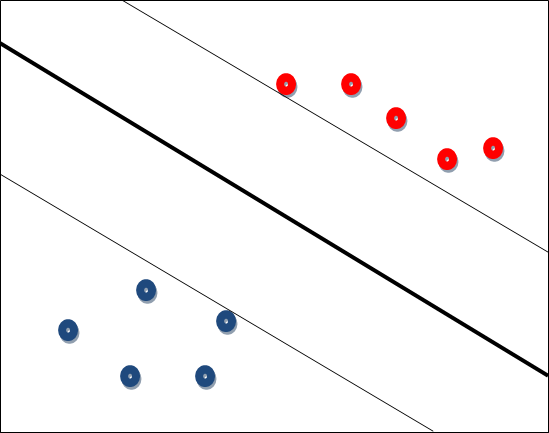
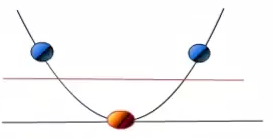
    如果需要分類的資料是線性可分的，比如說存在一條直線可以將座標系（二維）的兩類資料完全分離，或者延伸到存在一個超平面，可以將一個N維空間的資料完全分離。但我們知道這樣一條直線（超平面）是不唯一的。例如圖中的粗黑線：

問題在於，那種分類方案是最優的呢？這裡引入一個概念MMH：最大間隔分類器Maximum Margin Classifier，對一個數據點進行分類，當超平面離資料點的“間隔”越大，分類的確信度（confidence）也越大。所以，為了使得分類的確信度儘量高，需要讓所選擇的超平面能夠最大化這個“間隔”值。這個“間隔”值也就是粗線與細線（細線臨近資料點）的距離。那麼臨近細線的點，就叫做支援向量點。因此SVM有一個優點，就是即使有大量的資料，但是支援向量點是固定的，因此即使再次訓練大量資料，這個超平面也可能不會變化。

sklearn裡的SVM模組提供了這樣分類的方法（SVC）

SVC引數解釋 
（1）C: 目標函式的懲罰係數C，用來平衡分類間隔margin和錯分樣本的，default C = 1.0； 
（2）kernel：引數選擇有RBF, Linear, Poly, Sigmoid, 預設的是"RBF"; 
（3）degree：if you choose 'Poly' in param 2, this is effective, degree決定了多項式的最高次冪； 
（4）gamma：核函式的係數('Poly','Linear', 'RBF' and 'Sigmoid'), 預設是gamma = 1 / n_features; 
（5）coef0：核函式中的獨立項，'RBF' and 'Poly'有效； 
（6）probablity: 可能性估計是否使用(true or false)； 
（7）shrinking：是否進行啟發式； 
（8）tol（default = 1e - 3）: svm結束標準的精度; 
（9）cache_size: 制定訓練所需要的記憶體（以MB為單位）； 
（10）class_weight: 每個類所佔據的權重，不同的類設定不同的懲罰引數C, 預設的話自適應； 
（11）verbose: 跟多執行緒有關，不大明白啥意思具體； 
（12）max_iter: 最大迭代次數，default = 1， if max_iter = -1, no limited; 
（13）decision_function_shape ： ‘ovo’ 一對一, ‘ovr’ 多對多  or None 無, default=None 
（14）random_state ：用於概率估計的資料重排時的偽隨機數生成器的種子。 
 ps：7,8,9一般不考慮。 
 

# coding:utf-8  
from sklearn import svm  
import numpy as np  
import matplotlib.pyplot as plt  
  
#np.random.seed(0)   指定隨機引數，用於測試
x = np.r_[np.random.randn(20,2)-[2,2],np.random.randn(20,2)+[2,2]] #正態分佈來產生數字,設定偏移量
y = [0]*20+[1]*20 #分類標記 20個class0，20個class1  
print('x = ',x)
print('y = ',y)
clf = svm.SVC(kernel='linear') #svm.svc模組,kernel='linear'線性核函式   
clf.fit(x,y)  
  

#coef_存放回歸係數，intercept_存放截距
w = clf.coef_[0] #獲取w  
a = -w[0]/w[1] #斜率  
#畫圖劃線  
xx = np.linspace(-4,4) #影象區間
yy = a*xx-(clf.intercept_[0])/w[1] #xx帶入y，截距  

#畫出與點相切的線  
b = clf.support_vectors_[0]  
yy_down = a*xx+(b[1]-a*b[0])  
b = clf.support_vectors_[-1]  
yy_up = a*xx+(b[1]-a*b[0])  
  
print("W:",w)  
print("a:",a)  
  
print("support_vectors_:",clf.support_vectors_)  
print("clf.coef_:",clf.coef_)  
  
plt.figure(figsize=(8,4))  
#plt.xlabel("X")  
#plt.ylabel("Y")  
#plt.title("Test")  
plt.plot(xx,yy)  
plt.plot(xx,yy_down)  
plt.plot(xx,yy_up)  
plt.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=80)  
plt.scatter(x[:,0],x[:,1],c=y,cmap=plt.cm.Paired) #[:，0]列切片，第0列  
  
plt.axis('tight')  
  
plt.show()  

3.2非線性分類

    當面對非線性可解的分類時，我們需要把資料投放到更高的維度再分割。

如下圖：當f(x)=x時，這組資料是個直線，但是當我把這組資料變為f(x)=x^2時，這組資料就可以被紅線所分割了。
比如說，我這裡有一組三維的資料X=（x1,x2,x3），線性不可分割，因此我需要將他轉換到六維空間去。
因此我們可以假設六個維度分別是：x1,x2,x3,x1^2,x1*x2,x1*x3，當然還能繼續展開，但是六維的話這樣就足夠了。
新的決策超平面：d(Z)=WZ+b，解出W和b後帶入方程，因此這組資料的超平面應該是：
d(Z)=w1x1+w2x2+w3x3+w4*x1^2+w5x1x2+w6x1x3+b
轉換高緯度一般是以內積（dot product）的方式進行的，內積的演算法複雜度非常大。

SVC提供了其他非線性的核函式：（引數為kernel，預設為rbf）

enum { LINEAR, POLY, RBF, SIGMOID, PRECOMPUTED }; 
 LINEAR：線性核函式（linear kernel） → K(x,y)=x·y
 POLY:多項式核函式（ploynomial kernel）→ K(x,y)=[(x·y)+1]^d
 RBF:徑向機核函式(radical basis function) → K(x,y)=exp(-|x-y|^2/d^2）
 SIGMOID: 神經元的非線性作用函式核函式(Sigmoid tanh) → K(x,y)=tanh(a(x·y)+b）
 PRECOMPUTED：使用者自定義核函式

以下程式碼為以常見的iris測試資料，各核函式的分類檢視

# coding:utf-8  
  
import numpy as np  
import matplotlib.pyplot as plt  
from sklearn import svm, datasets  
  
iris = datasets.load_iris()  
X = iris.data[:, :2]  #萼片長寬 
y = iris.target    #類別  
C = 1e3 
svc = svm.SVC(kernel="linear").fit(X, y)  
rbf_svc = svm.SVC(kernel="rbf", gamma=0.1, C=C).fit(X, y)  
poly_svc = svm.SVC(kernel="poly", gamma=0.1,degree=2, C=C).fit(X, y)  
sigmoid_svc = svm.SVC(kernel="sigmoid",gamma=0.1,C=C).fit(X, y)
#在svm模組中還有一個較為簡單的線性分類函式：LinearSVC()，
#其不支援kernel引數，因為設計思想就是線性分類。
lin_svc =svm.LinearSVC(C=C).fit(X, y)  
X_min, X_max = X[:, 0].min() - 1, X[:, 0].max() + 1  
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1  
xx, yy = np.meshgrid(np.arange(X_min, X_max, 0.02),  
                     np.arange(y_min, y_max, 0.02))  
test_x = np.c_[xx.ravel(), yy.ravel()]  
titles = ['linear kernel',  
          'LinearSVC',  
          'RBF kernel',  
          'poly kernel',
          'sigmoid kernel']  

plt.figure(figsize=(8,4))  
for i, clf in enumerate((svc, lin_svc, rbf_svc, poly_svc,sigmoid_svc)):  
    plt.subplot(2, 3, i+1)  
    plt.subplots_adjust(wspace=0.4, hspace=0.4) 
    print(titles[i],':\n',clf,'\n')
    Z = clf.predict(test_x).reshape(xx.shape)  
    plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.5)   
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm)  
    plt.xlim(xx.min(), xx.max())  
    plt.ylim(yy.min(), yy.max())  
    plt.xticks(fontsize=10, color="darkorange")  
    plt.yticks(fontsize=10, color="darkorange")  
    plt.title(titles[i])  
  
plt.show()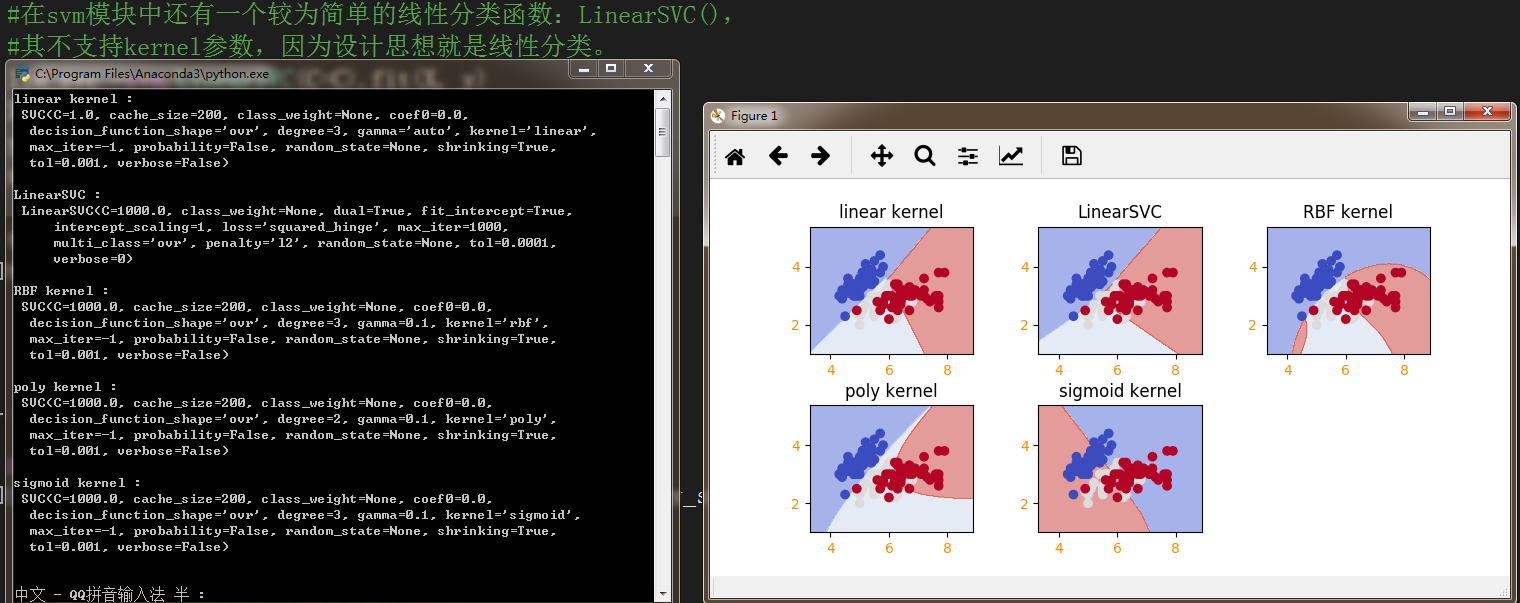  

四.迴歸

支援分類的支援向量機可以推廣到解決迴歸問題，這種方法稱為支援向量迴歸
支援向量分類所產生的模型僅僅依賴於訓練資料的一個子集，因為構建模型的成本函式不關心在超出邊界範圍的點，類似的，通過支援向量迴歸產生的模型依賴於訓練資料的一個子集，因為構建模型的函式忽略了靠近預測模型的資料集。
有三種不同的實現方式：支援向量迴歸SVR，nusvr和linearsvr。linearsvr提供了比SVR更快實施但只考慮線性核函式，而nusvr實現比SVR和linearsvr略有不同。
作為分類類別，訓練函式將X,y作為向量，在這種情況下y是浮點數

# coding:utf-8  
from sklearn import svm  
import numpy as np  
import matplotlib.pyplot as plt  
  
def f(x):
    return np.sin(x)/2

PI=3.1415926
x = np.sort(PI*2 * np.random.rand(40, 1) -PI, axis=0)  #產生40組資料，每組一個數據，axis=0決定按列排列，=1表示行排列  
y = f(x).ravel()   #np.sin()輸出的是列，和x對應，ravel表示轉換成行 

# 干擾資料 
y[::5] += 3 * (0.5 - np.random.rand(8))  

print('x = ',x)
print('y = ',y)
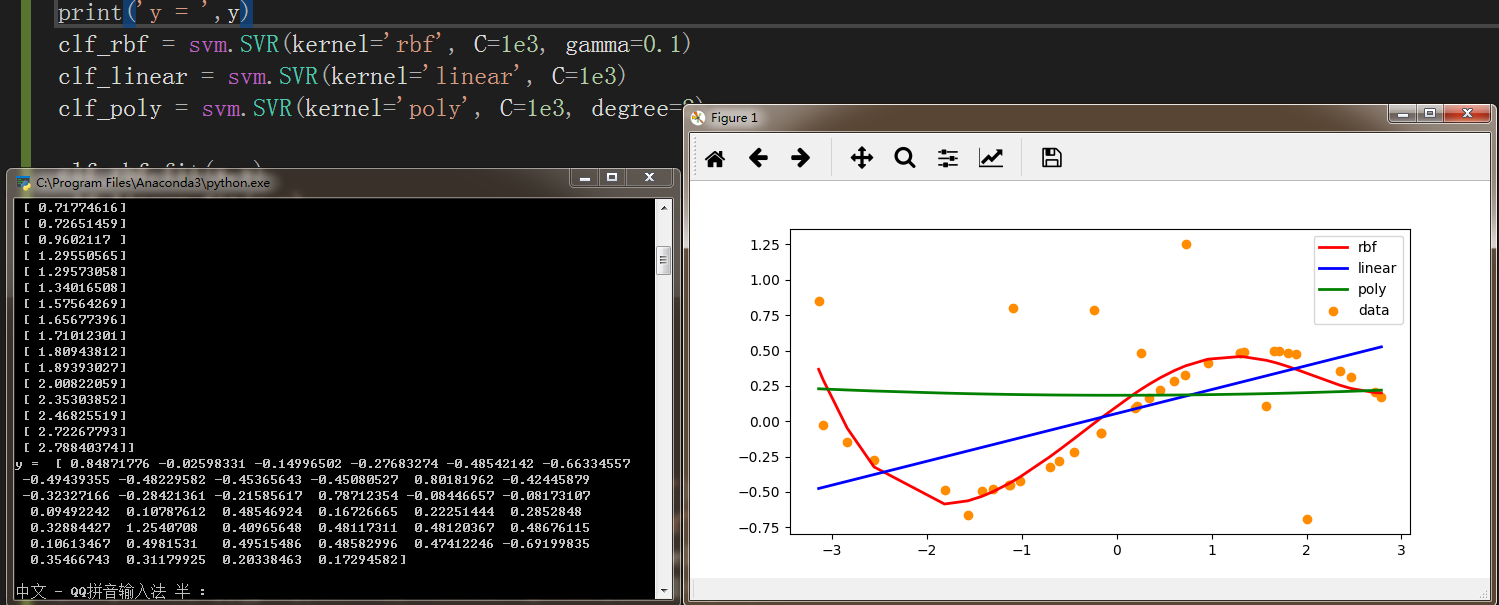
clf_rbf = svm.SVR(kernel='rbf', C=1e3, gamma=0.1) 
clf_linear = svm.SVR(kernel='linear', C=1e3) 
clf_poly = svm.SVR(kernel='poly', C=1e3, degree=2) 

clf_rbf.fit(x,y)  
clf_linear.fit(x,y)
clf_poly.fit(x,y)

yy_linear = clf_linear.predict(x)
yy_rbf = clf_rbf.predict(x)
yy_poly = clf_poly.predict(x) 
plt.figure(figsize=(8,4)) 


plt.scatter(x,y, color='darkorange',label='data')  
plt.plot(x, yy_rbf,lw = 2,color='red',label='rbf')  
plt.plot(x, yy_linear,lw = 2,  color='blue',label='linear')  
plt.plot(x, yy_poly,lw = 2,  color='green',label='poly')  
  
plt.axis('tight')  
plt.legend()
plt.show()  

五.總結

SVM方法是通過一個非線性對映p，把樣本空間對映到一個高維乃至無窮維的特徵空間中（Hilbert空間），使得在原來的樣本空間中非線性可分的問題轉化為在特徵空間中的線性可分的問題．簡單地說，就是升維和線性化．升維，就是把樣本向高維空間做對映，一般情況下這會增加計算的複雜性，甚至會引起“維數災難”，因而人們很少問津．但是作為分類、迴歸等問題來說，很可能在低維樣本空間無法線性處理的樣本集，在高維特徵空間中卻可以通過一個線性超平面實現線性劃分（或迴歸）．一般的升維都會帶來計算的複雜化，SVM方法巧妙地解決了這個難題：應用核函式的展開定理，就不需要知道非線性對映的顯式表示式；由於是在高維特徵空間中建立線性學習機，所以與線性模型相比，不但幾乎不增加計算的複雜性，而且在某種程度上避免了“維數災難”．這一切要歸功於核函式的展開和計算理論。

六.相關學習資源