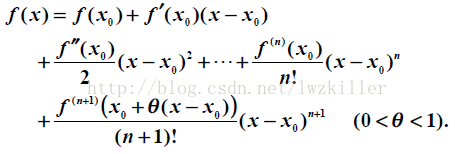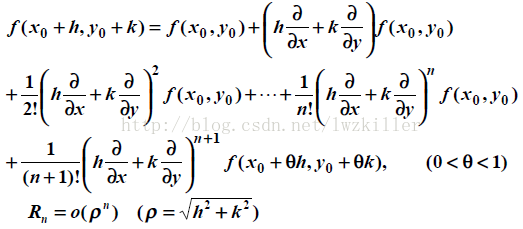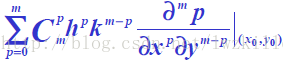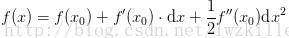Hessian矩陣以及在影象中的應用
Hessian Matrix,它有著廣泛的應用,如在牛頓方法、求極值以及邊緣檢測、消除邊緣響應等方面的應用。一個Hessian Matrix涉及到很多數學相關的知識點,比如泰勒公式、極值判斷、矩陣特徵值及特徵向量、二次型等。本篇文章,主要說明多元情況下的極值判定、hessian矩陣與二次型的聯絡以及有關hessian matrix在影象上的應用。
1. 二元函式泰勒公式
對於一元函式的泰勒公式,大家都有所瞭解,其意義是使用多次多項式來近似表達原函式f(x),一元函式的f(x)的泰勒公式如下:
在實際應用中,我們一般取前面幾階多項式的和來近似表達原函式f(x)。
然而,在影象處理中,我們應用的都是二元函式f(x,y),下面著重講解下二元函式的泰勒公式:
如果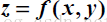
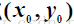

其中記號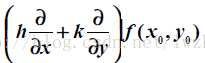
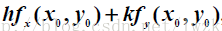
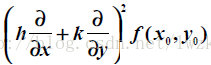
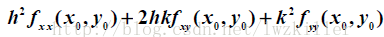
通用記號
人生苦短,關於這些公式這裡就不證明了,大家可以參考相關數學資料進行證明。
2. 極值判斷
如果對於函式中某一點其一階導數為0,二階導數不為0,那麼該點必定為極值點。再進一步分析,如果二階導數大於0,那麼該點為極小值點,如果二階導數小於0,那麼該點為極大值點。關於這些性質的描述,最直觀方法就是自己畫圖進行理解。另外可以通過表示式給予一些直觀理解(省略後面的多階餘項),雖然表示式並非嚴格,比如,對於一元函式進行泰勒公式展開並認定完全相等:
針對凸函式,如果在x0處的一階為0,二階為正,那麼我們就可以斷定f(x)肯定比在x0處的函式值大,我們可以認為x0為極小值點。對於影象中的二元函式呢?我們是可以類推的。根據上述二元泰勒公式可得二階近似表示式:
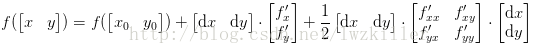
對於這種情形,這裡面會涉及到Hessian矩陣正定以及負定的判斷,這裡令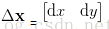

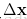
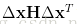
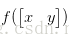

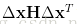
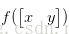
3. 二次型的性質
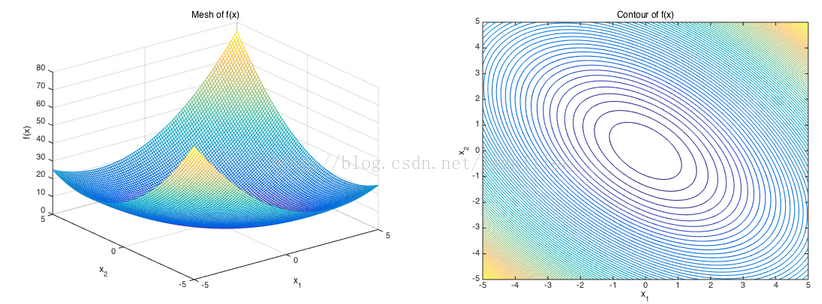
可以發現上面矩陣H即為Hessian矩陣,具有對稱性。而二次型的矩陣也是對稱的,接下來主要介紹下二次型最優化,以一個具體例子進行說明。
最小化二次型函式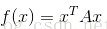
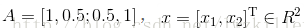
並且我們求得矩陣A的特徵向量[-0.7071,0.7071],[0.7071,0.7071],
我們可以知道等高線越密集的地方,說明函式值變化較快,而這個函式變化最快的方向即是特徵向量[0.7071,0.7071]所對應的方向;等高線越稀疏的地方,說明函式值變化較慢,而變化最慢的方向即是特徵向量[-0.7071,0.7071]所對應的方向,並且可以觀察矩陣特徵值的大小與函式值變化程度有關,較大特徵值所對應的特徵向量方向上的函式值變化最快,較小特徵值所對應的特徵向量方向上的函式值變化最慢。
這裡描述二次型的目的就是講解Hessian矩陣的特徵值以及特徵向量與二次型函式值變化之間的關係。其中二次型函式的二階偏導就構成了Hessian矩陣,也即是A矩陣。
4. 邊緣檢測以及邊緣響應消除
既然檢測到的對應點確認為邊緣點,那麼我們就有理由消除這個邊緣點,所以邊緣檢測與邊緣響應消除的應用是一回事。邊緣到底有什麼特徵呢?如下圖所示,一個二維平面上的一條直線,影象的特徵具體可以描述為:沿著直線方向,亮度變化極小,垂直於直線方向,亮度由暗變亮,再由亮變暗,沿著這個方向,亮度變化很大。我們可以將邊緣影象分佈特徵與二次型函式圖形進行類比,是不是發現很相似,我們可以找到兩個方向,一個方向影象梯度變化最慢,另一個方向影象梯度變化最快。那麼影象中的邊緣特徵就與二次型函式的影象對應起來了,其實二次型函式中的hessian矩陣,也是通過對二次型函式進行二階偏導得到的(可以自己求偏導測試下),這就是我們為什麼可以使用hessian矩陣來對邊緣進行檢測以及進行邊緣響應消除,我想大家應該明白其中的緣由了。還是那句話,數學模型其實就是一種反映影象特徵的模型。
所以Hessian matrix實際上就是多變數情形下的二階導數,他描述了各方向上灰度梯度變化,這句話應該很好理解了吧。我們在使用對應點的hessian矩陣求取的特徵向量以及對應的特徵值,較大特徵值所對應的特徵向量是垂直於直線的,較小特徵值對應的特徵向量是沿著直線方向的。對於SIFT演算法中的邊緣響應的消除可以根據hessian矩陣進行判定。
關於hessian的應用基本講完了,有問題可以留言討論。
參考文獻:
1.https://www.zhihu.com/question/40181086
2.https://zh.wikipedia.org/wiki/%E6%B5%B7%E6%A3%AE%E7%9F%A9%E9%98%B5
3.http://www.zhihujingxuan.com/18143.html
4.http://blog.sina.cn/dpool/blog/s/blog_5d2990b70101c1pc.html
5.http://blog.sina.com.cn/s/blog_790bb71901015087.html
6.http://painterlin.com/2015/09/12/Intuition-of-Eigen-Value.html
相關推薦
Hessian矩陣以及在影象中的應用
Hessian Matrix,它有著廣泛的應用,如在牛頓方法、求極值以及邊緣檢測、消除邊緣響應等方面的應用。一個Hessian Matrix涉及到很多數學相關的知識點,比如泰勒公式、極值判斷、矩陣特徵值及特徵向量、二次型等。本篇文章,主要說明多元情況下的極值判定、hessi
使用TensorFlow進行常用的影象處理-影象轉為矩陣以及影象大小調整1
影象編碼處理 將影象轉為一個三維矩陣,並使用三維矩陣形成一個影象: import tensorflow as tf import matplotlib.pyplot as plt # 讀取原始影象資料 image_raw_data = tf.gfile.FastGFi
使用TensorFlow進行常用的影象處理-影象轉為矩陣以及影象大小調整
影象編碼處理 將影象轉為一個三維矩陣,並使用三維矩陣形成一個影象: import tensorflow as tf import matplotlib.pyplot as plt # 讀取
RANSAC演算法以及影象演算法中的應用
Ransac的縮寫是Random Sample Consensus。 Ransac演算法的直線擬合算法大致步驟如下: k是迭代次數,n是每次取樣點個數,t是擬合的閾值,如果是直線擬合,可以理解為check的點到擬合出的直線距離,小於則是inliner否則為outliner。 如果迭
計算機視覺與影象:八大熱點公司以及九大應用場景
根據 IT 桔子資料,國內人工智慧產業中「計算機視覺與影象」領域的公司數量已達 111 家,僅次於「自然語言處理」類公司,位居第二。 我們將那些核心技術為「將深度學習技術應用於視覺與影象領域」的公司歸到「計算機視覺與影象」類。同時,「無人機」和「機器人」相關公司並未被統計在內,這部分公司雖然也會
最近鄰插值和雙線性插值的基本原理 以及OpenCV中resize函式的用法改變影象的大小
最近鄰插值和雙線性插值的基本原理 影象的縮放很好理解,就是影象的放大和縮小。傳統的繪畫工具中,有一種叫做“放大尺”的繪畫工具,畫家常用它來放大圖畫。當然,在計算機上,我們不再需要用放大尺去放大或縮小影象了,把這個工作交給程式來完成就可以了。下面就來講講計算機怎麼來放大縮小圖象;在本文中,
求3D影象Hessian矩陣特徵值 ITK
還沒有親測,先放著,因為要用這個...... Eigenvalues of Hessian Matrix are used as a criteria for line-like structure such as pulmonary vessels and fungi vessels.ITK
Git-Flow 的個人理解以及專案中的實際應用
Tip:不需要了解git-flow思想和概念的同學可以直接忽略文字部分直接進入程式碼講解流程 首先git-flow是對git程式碼管理的一種特殊應用,主要是應用於多人協作開發的專案流程中.和git的使用沒有本質區別,git-flow可以理解為是使用指令碼對gi
【資訊科技】【2011】【含部分原始碼】影象處理和機器學習技術在數字乳腺影象中癌組織檢測與分類的應用
本文為馬來西亞馬來亞大學(作者:JAWAD NAGI)的電腦科學碩士論文,共355頁。 乳腺癌是最常見的癌症之一,也是導致女性死亡的主要原因。乳腺攝影是目前最有效的乳腺癌影像學檢查方法,可用於鑑別異常癌細胞。研究顯示,在當前的乳腺癌篩查中,大約15%到30%的
裝飾器 以及 django 中的應用
裝飾器本質上是一個Python函式,它可以讓其他函式在不需要做任何程式碼變動的前提下增加額外功能,裝飾器的返回值也是一個函式物件。它經常用於有切面需求的場景,比如:插入日誌、效能測試、事務處理、快取、許可權校驗等場景。裝飾器是解決這類問題的絕佳設計,有了裝飾器,我們就可以抽離出大量與函式功能本身無關的雷
稀疏矩陣在opencv中的應用(大矩陣運算速度過慢的問題,藉助SparseMat?)
大矩陣相乘的問題 很多演算法在執行的過程中產生的大矩陣往往包含很多0元素,我們下面的內容也是主要針對這類矩陣展開的。所以這個問題換一個說法就是 稀疏矩陣在opencv中的應用 可以看出,opencv確實支援稀疏矩陣,也就是SparseMat,
Lines_gauss——檢測影象中的線條及其寬度,在視覺表面檢測方面應用廣泛。
lines_gauss(Image : Lines : Sigma, Low, High, LightDark, ExtractWidth, LineModel, CompleteJunctions : ) Image:輸入影象 Lines:提取出的亞畫素
python 中的 常用 opencv 以及影象處理相關函式總結整理
1.讀取圖片 img = cv2.imread("D:\cat.jpg") ,OpenCV目前支援讀取bmp、jpg、png、tiff等常用格式。 建立一個視窗 cv2.namedWindow("Image") 然後在視窗中顯示影象 cv2.ims
梯度、Hessian矩陣、平面方程的法線以及函式導數的含義
想必單獨論及“ 梯度、Hessian矩陣、平面方程的法線以及函式導數”等四個基本概念的時候,絕大部分人都能夠很容易地談個一二三,基本沒有問題。 其實在應用的時候,這幾個概念經常被混淆,本文試圖把這幾個概念之間的關係整理一下,以便應用之時得心應手。 這四個概念中,Hessia
opencv3逼近多邊形曲線-approxPolyDP函式在影象中的應用
#include<opencv2/opencv.hpp> #include<iostream> #include<vector> using namespace cv; using namespace std; int main()
三種條碼code39和code93以及code128在應用中的比較
與經常在商品上見到的ENA 13條碼不同,code39, code93和 code128常用於企業自定義編碼的應用。 從易用性來說,code39顯示是最容易的,其編碼只需要對原字串前後加上符號“*”即可。code93作為code39的改進,複雜程居中,到目前還沒在實際
霍夫變換在影象處理中的應用(尋找影象中的直線)
一、原理 參考霍夫變換,如果有課本的話參考岡薩雷斯的影象處理課本及matlab版本的課本最好,如果沒有就看下這節的原理描述。 直角座標系中對於直線方程有如下等式: ρ=x∗cosθ+y∗sinθ(ρ≥0) 其中ρ為座標原點到直線的距離,θ為ρ 與x軸正
影象處理 之 探索 與 驗證 拉普拉斯運算元(Laplace)與 Hessian矩陣特徵值 之間的關係
目錄 引言 5.結論 引言 數學:驗證矩陣對角線元素和等於特徵值之和 應用而言:給定影象,計算他的H
opencv3尋找最小包圍圓形在影象中的應用-滾動條
#include<opencv2/opencv.hpp> #include<iostream> #include<vector> using namespace cv; using namespace std; int g_nMinT
《計算機視覺與影象:八大熱點公司以及九大應用場景》
根據 IT 桔子資料,國內人工智慧產業中「計算機視覺與影象」領域的公司數量已達 111 家,僅次於「自然語言處理」類公司,位居第二。我們將那些核心技術為「將深度學習技術應用於視覺與影象領域」的公司歸到「計算機視覺與影象」類。同時,「無人機」和「機器人」相關公司並未被統計在內,這部分公司雖然也會涉及到計算機視覺