最近參加2016華為軟體精英挑戰賽，題目也比較直接，就是求過定點的最短路。這題和以前練得不一樣，感覺是不是要用DP(動態規劃)。可是對於DP演算法，我還是啥都不懂，於是好好補補。

看完入門，有點感覺了，然後是LIS問題，文中又提到了LCS問題，說這個更基礎，於是轉去看LCS。

這張圖是演算法關鍵：

注意這裡的C[i][j]，x[i],y[j]下標含義一樣，指向相同的位置～

看完LCS，就拿poj1458練練手：

//time:16MS
//mem:396K

#include <string>
#include <iostream>
#include <vector>

using namespace std;

inline int max(int a, int b)
{
	return a > b ? a : b;
}

int LCS(const string x, const string y)
{
	int m, n, i, j;
	m = x.length();
	n = y.length();

	vector<vector<int> > table(m + 1, vector<int>(n + 1));
	
	for(i = 0; i < m + 1; ++i)
	{
		for(j = 0; j < n + 1; ++j)
		{
			if(i == 0 || j == 0)
				table[i][j] = 0;
			else if(x[i - 1] == y[j - 1])
				table[i][j] = table[i - 1][j - 1] + 1;
			else
				table[i][j] = max(table[i - 1][j], table[i][j - 1]);
		}
	}
	
	return table[m][n];
}

int main()
{
	string x, y;
	while(cin >> x)
	{
		cin >> y;
		cout << LCS(x, y) << endl;
	}
	return 0;
}
 

接著返回我們的 LIS問題：

最關鍵的狀態轉移方程如下：

設 A[i] 是該序列，並用 D[i] 表示以A[i]結尾的最長非降子序列的長度：
D[j] = max {1, A[i] + 1}，if A[j] >= A[i]，其中 i < j

此時，我們可以拿 leetcode #300 Longest Increasing Subsequence 練練手：

//leetcode300 Longest Increasing Subsequence
//144ms
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int i, j, len = 1, SIZE = nums.size();

	if(!nums.size())	//防止陣列為空
		return 0;

	vector<int> D(SIZE, 1);

	for(i = 1; i < SIZE; ++i)
	{
		for(j = 0; j <= i - 1; ++j)
		{
			if(nums[j] < nums[i] && D[j] + 1 > D[i]) //遞增序列，若求非降子序列，改nums[j] <= nums[i]
				D[i] = D[j] + 1;

			if(len < D[i])
			len = D[i];
		}
	}

	return len;
    }
};
 

//leetcode300 Longest Increasing Subsequence
//4 ms
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int i, j, maxLen = 1, SIZE = nums.size();
		
		if(!nums.size())
		    return 0;
		
		vector<int> D(SIZE, 1);
		D[1] = nums[0];
		D[0] = 0;	//此處設定要讓D[0]小於數組裡的所有值，此處的0感覺還是大了，不過居然過了。。巧合吧	
		for(i = 1; i < SIZE; ++i){
		    if(nums[i] > D[maxLen])
		        D[++maxLen] = nums[i];
		    else
		        for(j = maxLen; j >= 1; --j){
		            if(D[j] >= nums[i] && D[j-1] < nums[i]){  //找到陣列D裡第一個剛好小於nums[i]的值，替換之
		                D[j] = nums[i];
		                break;
		            }	    
		        }            
		}
		
		return maxLen;
    }
};

注意在該題中，子序列是遞增的，而非非降子序列，所以與我們上面的公式稍微有所不同。我們還要注意裡面的下標，還是依據C裡面下標從0開始這一規則。

接著是二維DP問題，突然回想起LCS不就是個二維DP解法嗎。。

可以用 leetcode 上 Unique Path I & II練手：

//Unique Path I
//0 ms
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int> > D(m, vector<int>(n));
        int i, j;
        
        if((m && n) == 0)	//防止原矩陣為空
            return 0;
        
        for(i = 0; i < m; ++i)
            D[i][0] = 1;
        for(i = 0; i < n; ++i)
            D[0][i] = 1;
            
        for(i = 1; i < m; ++i)
            for(j = 1; j < n; ++j)
                D[i][j] = D[i - 1][j] + D[i][j - 1];
        
        return D[m-1][n-1];
    }
};

//Unique Path II
//4 ms
class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        
        if((m && n) == 0)
            return 0;
        
        int i, j;
        vector<vector<int> > D(m, vector<int>(n, 0));
        
        for(i = 0; i < m; ++i)
            if(!obstacleGrid[i][0])
                D[i][0] = 1;
            else
                break;
                
        for(i = 0; i < n; ++i)
            if(!obstacleGrid[0][i])
                D[0][i] = 1;
            else
                break;
            
        for(i = 1; i < m; ++i)
            for(j = 1; j < n; ++j)
                if(!obstacleGrid[i][j])
                    D[i][j] = D[i - 1][j] + D[i][j - 1];
        
        return D[m - 1][n - 1];
            
        }
};

然後是帶有額外條件的DP問題：題解巧妙地使用陣列下標，立刻讓我們對問題的解清晰不少，這其實顯示瞭解題者挖掘出了題目中的一些性質。

題目：

無向圖G有N個結點，它的邊上帶有正的權重值。

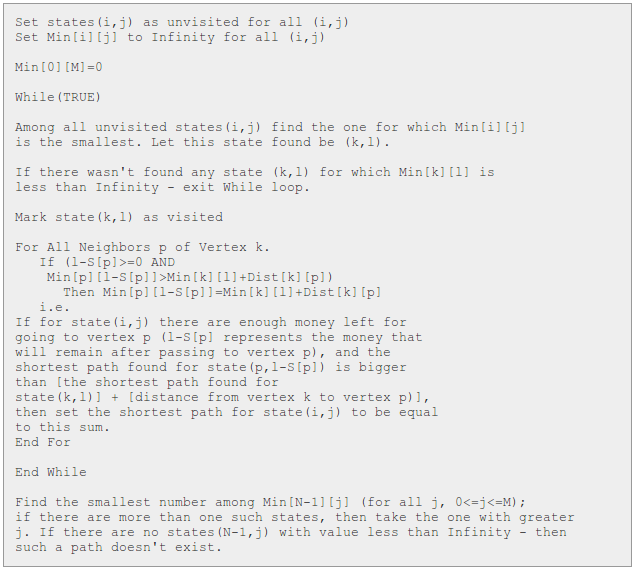
你從結點1開始走，並且一開始的時候你身上帶有M元錢。如果你經過結點i， 那麼你就要花掉S[i]元(可以把這想象為收過路費)。如果你沒有足夠的錢， 就不能從那個結點經過。在這樣的限制條件下，找到從結點1到結點N的最短路徑。 或者輸出該路徑不存在。如果存在多條最短路徑，那麼輸出花錢數量最少的那條。 限制：1<N<=100 ; 0<=M<=100 ; 對於每個i，0<=S[i]<=100；正如我們所看到的， 如果沒有額外的限制條件(在結點處要收費，費用不足還不給過)，那麼， 這個問題就和經典的迪傑斯特拉問題一樣了(找到兩結點間的最短路徑)。 在經典的迪傑斯特拉問題中， 我們使用一個一維陣列來儲存從開始結點到每個結點的最短路徑的長度， 即M[i]表示從開始結點到結點i的最短路徑的長度。然而在這個問題中， 我們還要儲存我們身上剩餘多少錢這個資訊。因此，很自然的， 我們將一維陣列擴充套件為二維陣列。

題解：

我們用M[i][j]表示從開始結點到結點i的最短路徑長度， 且剩餘j元。通過這種方式，我們將這個問題規約到原始的路徑尋找問題。 在每一步中，對於已經找到的最短路徑，我們找到它所能到達的下一個未標記狀態(i,j)， 將它標記為已訪問(之後不再訪問這個結點)，並且在能到達這個結點的各個最短路徑中， 找到加上當前邊權重值後最小值對應的路徑，即為該結點的最短路徑。 (寫起來真是繞，建議畫個圖就會明瞭很多)。不斷重複上面的步驟， 直到所有的結點都訪問到為止(這裡的訪問並不是要求我們要經過它， 比如有個結點收費很高，你沒有足夠的錢去經過它，但你已經訪問過它) 最後Min[N-1][j]中的最小值即是問題的答案(如果有多個最小值， 即有多條最短路徑，那麼選擇j最大的那條路徑，即，使你剩餘錢數最多的最短路徑)。

讀著挺繞的，要試著走一遍過程，我花了好幾個小時。。。其實過程和 Dijkstra 演算法還是蠻相似的，在每一階段的狀態變化還是服從距離最短這一要點，同時保證錢的限制，所以增加了"剩餘錢量"那一維度，所以為了能夠在路徑一樣短時可以比較不同路徑所所花的錢，我們把判斷是否 visited 過的物件從點變成了 Min[][] 陣列。注意到與 Dijkstra 演算法的相同點與不同點即可。

不過，感覺此題的複雜度貌似不低。

最後是高階DP，它高在我們要仔細揣摩題目，將其規約為DP問題。

終於看完，收穫很多。DP演算法核心就在於將一個大問題的分成一個一個的階段，即一個一個小問題（狀態），然後試著解決它（狀態轉移方程）。狀態與狀態轉移方程缺一不可。如果看起來是個DP問題，但你卻無法定義出狀態， 那麼試著將問題規約到一個已知的DP問題。此外，我們還看出了DP演算法與BFS，貪心演算法的聯絡與區別。