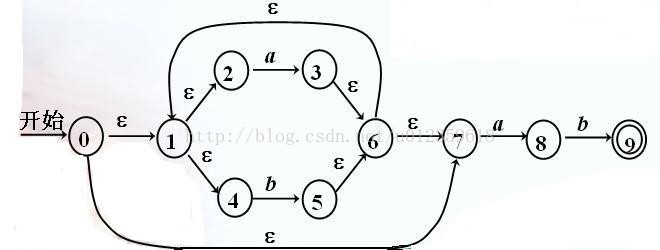
1. 根據上面的狀態轉換圖寫出狀態轉換表，什麼！不知道什麼是狀態轉換表？那你來對地方了。狀態轉換表是轉檯轉換圖的另外一種表示形式，如下圖，左側表頭0~9表示的

    是狀態，上方表頭a,b,c表示的是條件。其餘部分表示的是後繼狀態

ε-closure(0)={0,1,2,4,7}

ε-closure(1)={1,2,4}

ε-closure(2)={2}

ε-closure(3)={1,2,3,4,6,7}

ε-closure(4)={4}

ε-closure(5)={1,2,4,5,6,7}

ε-closure(6)={1,2,4,6,7}

ε-closure(7)={7}

ε-closure(8)={8}

ε-closure(9)={9}

3. 轉換，下面就是真正劇情了

首先將初始態的轉換閉包ε-closure(0)設為狀態A，即A={0,1,2,4,7}，注意這裡的狀態A是DFA中的，和前面的狀態0,1,2,3,4,5沒有關係

接著寫出狀態A經過上面轉換圖中所有轉換條件得到的狀態，後繼狀態裡面不包括自身，這裡的轉換條件包括a和b，注意，不包括ε，轉換的一個目的就是消除ε。

ε-closure(0) = A

ε-closure(move(A,a)) = ε-closure({3,8}) = {1,2,3,4,6,7,8} = B

ε-closure(move(A,b)) = ε-closure(5) = {1,2,4,5,6,7} = C

ε-closure(move(B,a)) = ε-closure({3,8}) = {1,2,3,4,6,7,8} = B

ε-closure(move(B,b)) = ε-closure({5,9}) = {1,2,4,5,6,7,9} = D

ε-closure(move(C,a)) = ε-closure()

ε-closure(move(C,b))

ε-closure(move(D,a)) = ε-closure({3,8}) = {1,2,3,4,6,7,8} = B

ε-closure(move(D,b)) = ε-closure(5) = {1,2,4,5,6,7} = C

4. 畫出DFA狀態轉換表（每一個狀態只有一個後繼狀態）

5. 畫出DFA狀態轉換圖

4.DFA的最小化

    （1） 消除多餘狀態

              Ⅰ. 什麼是多餘狀態

                    · 從這個狀態出發沒有通路到達終態

                    ·  從開始狀態出發，任何輸入串也不能到達的那個狀態

               Ⅱ. 如何消除多餘狀態

                     刪除

             （2）  等價狀態

                      Ⅰ. 何為等價狀態，對於兩個狀態s和t

                            ·  一致性條件：狀態s和t必須同時為終態或非終態

                            ·  蔓延性條件：對於所有輸入符號，狀態s和狀態t必須轉化到等價的狀態裡

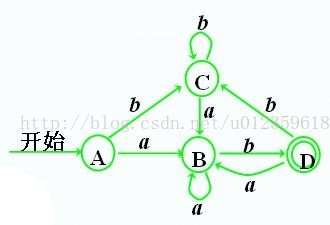
                   接下來是關於如何利用上面的兩個條件來判斷是否為等價狀態，來一張複雜的狀態轉換圖，是不是有點暈，哈哈

                   首先，畫出狀態轉換表

                  看1和2，1和2都是非終態，滿足條件1，1和2都可以轉換成狀態2，滿足條件2，將兩者合併。

                  看6和7，6和7都是終態，滿足條件2，6和7都可以轉化成狀態6，滿足條件2，將兩者合併。

                  以此類推，當然，2和5也是可以合併的，記住最後的結果只有一種，只要滿足合併後的狀態最少就行

                   轉化

                  1,2→A

                   3,4→B

                   5→C

                   6,7→D

                   列出轉化後的轉檯轉換表

                 再畫出相應的狀態轉換圖就大功告成啦~~

5.有限自動機與正規式之間的轉換

1．有限自動機轉換為正規式

對於 ∑上的NFAM，可以構造一個 ∑上的正規式R，使得L(R)=L(M)。拓廣狀態轉換圖的概念，令每條弧可用一個正規式作標記。為 ∑上的NFA M構造相應的正規式R，分為如下兩步：

（1）在M的狀態轉換圖中加兩個節點，一個x節點，一個y節點。從x節點到NFA M的初始狀態節點引一條弧並用 ε標記，從NFA M的所有終態節點到y節點引一條弧並用 ε標記。形成一個與 M等價的M'，M'只有一個初態x和一個終態y。

（2）按下面的方法逐步消去M'中除x和y的所有節點。在消除節點的過程中，用正規式來標記弧，最後節點x和y之間弧上的標記就是所求的正規式。消除節點的規則如圖2-6所示。

圖 2-6 有限自動機到正規式的轉換規則示意圖

2．正規式轉換為有限自動機

同樣地，對於 ∑上的每個正規式R，可以構造一個E上的NFA M，使得L(M)=L(R)。通過對正規式R進行分裂並加入新的節點，逐步把圖轉變成每條弧上的標記是E上的一個字元或 ε。轉換規則如圖2-7所示。

圖 2-7 正規式到有限自動機的轉換規則示意圖

然後觀察5出去的兩條邊（對應於.後的字元），如果是數字的話，就不能出現E了，所以選C。

具體來說

0是入口，6是出口,初始進入0狀態，必需最終到達6狀態
A 3857,狀態過程：0->1->1->1->1
B 1.2E+5,E+5狀態過程：0->1->5->2->? 
C -123.67,狀態過程：0->4->1->1->1->5->6->6

D 0.576E10，狀態過程：0->1->5->6->6->6->?