1. 詳解

STL (Seasonal-Trend decomposition procedure based on Loess) [1] 為時序分解中一種常見的演算法，基於LOESS將某時刻的資料\(Y_v\)分解為趨勢分量（trend component）、週期分量（seasonal component）和餘項（remainder component）:
\[ Y_v = T _v + S_v + R_v \quad v= 1, \cdots, N \]

STL分為內迴圈（inner loop）與外迴圈（outer loop），其中內迴圈主要做了趨勢擬合與週期分量的計算。假定\(T_v^{(k)}\)

• \(n_{(i)}\)內層迴圈數，
• \(n_{(o)}\)外層迴圈數，
• \(n_{(p)}\)為一個週期的樣本數，
• \(n_{(s)}\)為Step 2中LOESS平滑引數，
• \(n_{(l)}\)為Step 3中LOESS平滑引數，
• \(n_{(t)}\)為Step 6中LOESS平滑引數。

每個週期相同位置的樣本點組成一個子序列（subseries），容易知道這樣的子序列共有共有\(n_(p)\)個，我們稱其為cycle-subseries。內迴圈主要分為以下6個步驟：

• Step 1: 去趨勢（Detrending），減去上一輪結果的趨勢分量，\(Y_v - T_v^{(k)}\)；
• Step 2: 週期子序列平滑（Cycle-subseries smoothing），用LOESS (\(q=n_{n(s)}\), \(d=1\))對每個子序列做迴歸，並向前向後各延展一個週期；平滑結果組成temporary seasonal series，記為$C_v^{(k+1)}, \quad v = -n_{(p)} + 1, \cdots, -N + n_{(p)} $；
• Step 3: 週期子序列的低通量過濾（Low-Pass Filtering），對上一個步驟的結果序列\(C_v^{(k+1)}\)
  依次做長度為\(n_(p)\)、\(n_(p)\)、\(3\)的滑動平均（moving average），然後做LOESS (\(q=n_{n(l)}\), \(d=1\))迴歸，得到結果序列\(L_v^{(k+1)}, \quad v = 1, \cdots, N\)；相當於提取週期子序列的低通量；
• Step 4: 去除平滑週期子序列趨勢（Detrending of Smoothed Cycle-subseries），\(S_v^{(k+1)} = C_v^{(k+1)} - L_v^{(k+1)}\)；
• Step 5: 去週期（Deseasonalizing），減去週期分量，\(Y_v - S_v^{(k+1)}\)；
• Step 6: 趨勢平滑（Trend Smoothing），對於去除週期之後的序列做LOESS (\(q=n_{n(t)}\), \(d=1\))迴歸，得到趨勢分量\(T_v^{(k+1)}\)。

外層迴圈主要用於調節robustness weight。如果資料序列中有outlier，則餘項會較大。定義
\[ h = 6 * median(|R_v|) \]

對於位置為\(v\)的資料點，其robustness weight為
\[ \rho_v = B(|R_v|/h) \]
其中\(B\)函式為bisquare函式：
\[ B(u) = \left \{ { \matrix { {(1-u^2)^2 } & {for \quad 0 \le u < 1} \cr { 0} & {for \quad u \ge 1} \cr } } \right. \]
然後每一次迭代的內迴圈中，在Step 2與Step 6中做LOESS迴歸時，鄰域權重（neighborhood weight）需要乘以\(\rho_v\)，以減少outlier對迴歸的影響。STL的具體流程如下：

outer loop:
    計算robustness weight;
    inner loop:
        Step 1 去趨勢;
        Step 2 週期子序列平滑;
        Step 3 週期子序列的低通量過濾;
        Step 4 去除平滑週期子序列趨勢;
        Step 5 去週期;
        Step 6 趨勢平滑;

為了使得演算法具有足夠的robustness，所以設計了內迴圈與外迴圈。特別地，當\(n_{(i)}\)足夠大時，內迴圈結束時趨勢分量與週期分量已收斂；若時序資料中沒有明顯的outlier，可以將\(n_{(o)}\)設為0。

R提供STL函式，底層為作者Cleveland的Fortran實現。Python的statsmodels實現了一個簡單版的時序分解，通過加權滑動平均提取趨勢分量，然後對cycle-subseries每個時間點資料求平均組成周期分量：

def seasonal_decompose(x, model="additive", filt=None, freq=None, two_sided=True):
    _pandas_wrapper, pfreq = _maybe_get_pandas_wrapper_freq(x)
    x = np.asanyarray(x).squeeze()
    nobs = len(x)
    ...
    if filt is None:
      if freq % 2 == 0:  # split weights at ends
        filt = np.array([.5] + [1] * (freq - 1) + [.5]) / freq
        else:
          filt = np.repeat(1./freq, freq)

    nsides = int(two_sided) + 1
    # Linear filtering via convolution. Centered and backward displaced moving weighted average.
    trend = convolution_filter(x, filt, nsides)
    if model.startswith('m'):
        detrended = x / trend
    else:
        detrended = x - trend

    period_averages = seasonal_mean(detrended, freq)

    if model.startswith('m'):
        period_averages /= np.mean(period_averages)
    else:
        period_averages -= np.mean(period_averages)

    seasonal = np.tile(period_averages, nobs // freq + 1)[:nobs]

    if model.startswith('m'):
        resid = x / seasonal / trend
    else:
        resid = detrended - seasonal

    results = lmap(_pandas_wrapper, [seasonal, trend, resid, x])
    return DecomposeResult(seasonal=results[0], trend=results[1],
                           resid=results[2], observed=results[3])

R版STL分解帶噪音點資料的結果如下圖：

data = read.csv("artificialWithAnomaly/art_daily_flatmiddle.csv")
View(data)
data_decomp <- stl(ts(data[[2]], frequency = 1440/5), s.window = "periodic", robust = TRUE)
plot(data_decomp)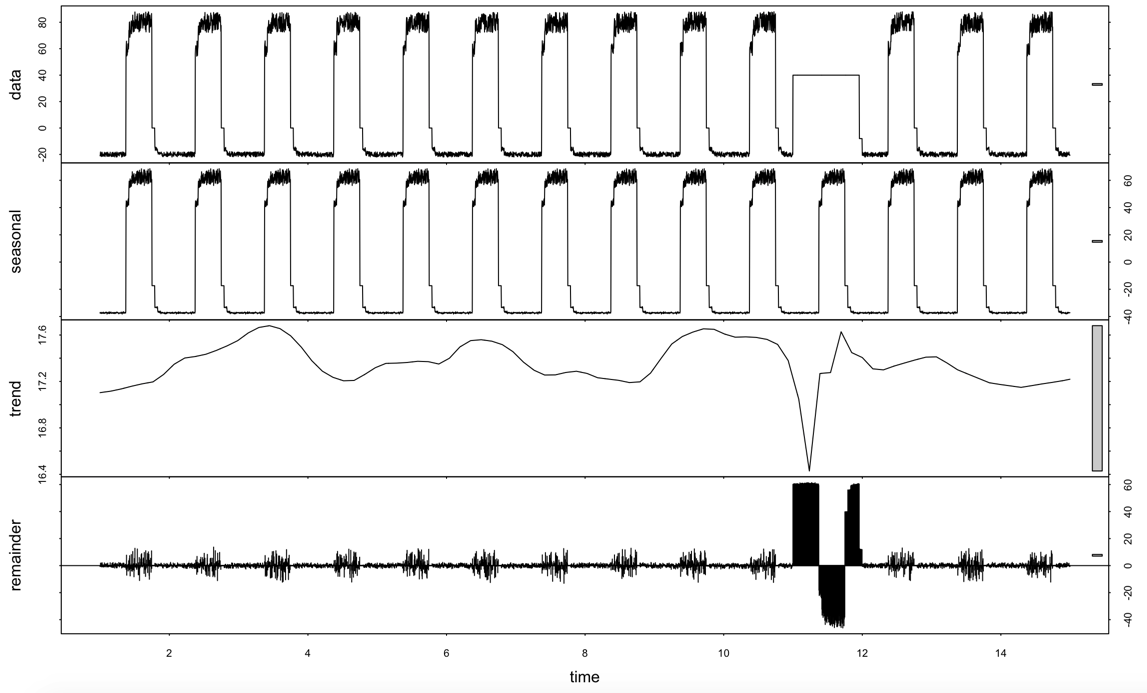

statsmodels模組的時序分解的結果如下圖：

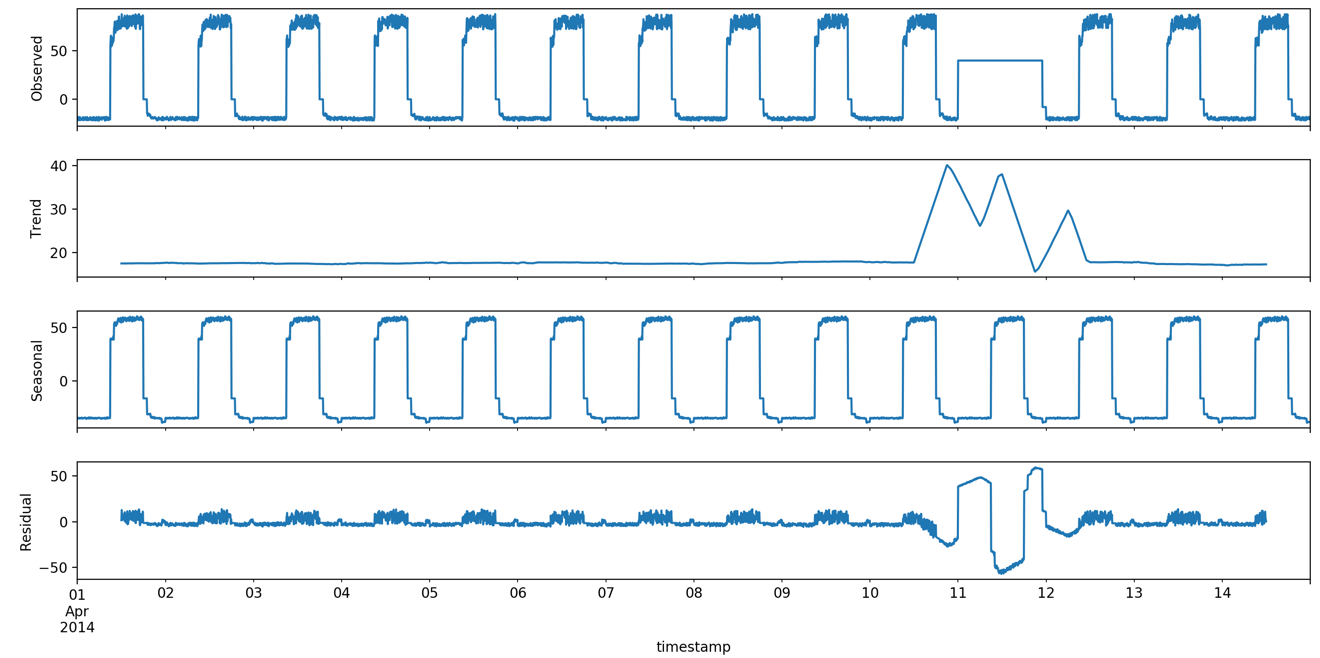
import statsmodels.api as sm
import matplotlib.pyplot as plt
import pandas as pd
from date_utils import get_gran, format_timestamp


dta = pd.read_csv('artificialWithAnomaly/art_daily_flatmiddle.csv',
                                   usecols=['timestamp', 'value'])
dta = format_timestamp(dta)
dta = dta.set_index('timestamp')
dta['value'] = dta['value'].apply(pd.to_numeric, errors='ignore')
dta.value.interpolate(inplace=True)
res = sm.tsa.seasonal_decompose(dta.value, freq=288)
res.plot()
plt.show()

2. 參考資料

[1] Cleveland, Robert B., William S. Cleveland, and Irma Terpenning. "STL: A seasonal-trend decomposition procedure based on loess." Journal of Official Statistics 6.1 (1990): 3.