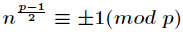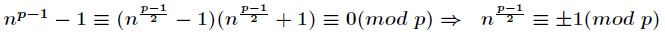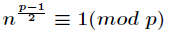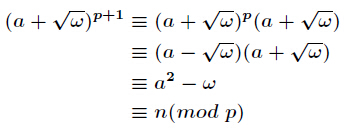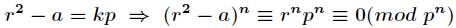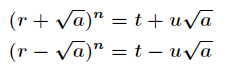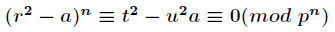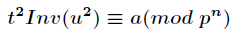[求解二次剩餘 數論技巧 隨機化] Ural 1132 Square Root
今天要討論的問題是解方程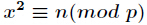
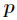
引理:
證明:由費馬小定理,
引理:方程有解當且僅當
定理:設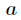
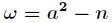
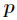
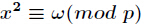
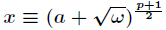
剩餘方程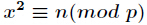
證明:由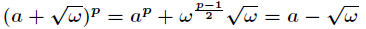
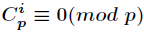
號用了費馬小定理和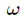
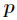
在演算法實現的時候,對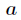
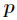
#include<cstdio> #include<cstdlib> #include<algorithm> using namespace std; typedef long long ll; inline char nc(){ static char buf[100000],*p1=buf,*p2=buf; if (p1==p2) { p2=(p1=buf)+fread(buf,1,100000,stdin); if (p1==p2) return EOF; } return *p1++; } inline void read(ll &x){ char c=nc(),b=1; for (;!(c>='0' && c<='9');c=nc()) if (c=='-') b=-1; for (x=0;c>='0' && c<='9';x=x*10+c-'0',c=nc()); x*=b; } ll P; inline ll Pow(ll a,ll b){ ll ret=1; for (;b;b>>=1,a=a*a%P) if (b&1) ret=ret*a%P; return ret; } inline ll legendre(ll a){ return Pow(a,(P-1)>>1); } struct abcd{ ll a,b,w; //a+b*sqrt(w) abcd(ll a=0,ll b=0,ll w=0):a(a),b(b),w(w) { } friend abcd operator *(abcd A,abcd B){ return abcd((A.a*B.a%P+A.b*B.b%P*A.w%P)%P,(A.a*B.b%P+A.b*B.a%P)%P,A.w); } }; inline abcd Pow(abcd a,int b){ abcd ret=abcd(1,0,a.w); for (;b;b>>=1,a=a*a) if (b&1) ret=ret*a; return ret; } inline ll Solve(ll n,ll p){ P=p; if (P==2) return 1; if (legendre(n)==P-1) return -1; ll a,w; while (1){ a=rand()%P; w=((a*a-n)%P+P)%P; if (legendre(w)==P-1) break; } return Pow(abcd(a,1,w),(P+1)>>1).a; } int main(){ srand(10086); ll n,p,T,ans,a,b; freopen("t.in","r",stdin); freopen("t.out","w",stdout); read(T); while (T--){ read(n); read(p); ans=Solve(n,p); if (ans==-1) printf("No root\n"); else if (ans==p-ans) printf("%lld\n",ans); else if (ans<P-ans) printf("%lld %lld\n",ans,P-ans); else printf("%lld %lld\n",P-ans,ans); } return 0; }
接下來我們來解另一個二次同餘方程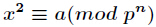
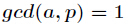
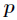
先求出方程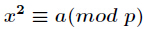
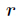
我們知道
那麼也就是說
可以證明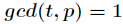
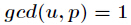
這裡由於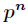
相關推薦
[求解二次剩餘 數論技巧 隨機化] Ural 1132 Square Root
今天要討論的問題是解方程,其中是奇質數。 引理: 證明:由費馬小定理, 引理:方程有解當且僅當 定理:設滿足不是模的二次剩餘,即無解,那麼是二次 剩餘方程的解。
[斐波那契數列 求解二次剩餘&二次模方程 BSGS] COGS 2114 [CodeChef FN]斐波那契數
我們可以考慮斐波那契的通項公式 換元可以轉化成一個二次方程 根據求根公式求出後 再用BSGS求出指數 注意分奇偶考慮 #include<cstdio> #include<cstdlib> #include<algorithm> #in
【模板】【證明】任意模數下的二次剩餘求解
什麼是二次剩餘問題 就是求解形如 x 2
2018.12.30【NOIP訓練】任意模數二次剩餘(高階數論大雜燴)
描述 求解關於xx的方程: x 2
cdqz2017-test1-數論 (BSGS + 二次剩餘 + CRT)
#include<map> #include<cmath> #include<cstdio> #include<iostream> using namespace std; map<int,int>mp; int Pow(
《數論概論》讀書筆記 第23章 二次剩餘
什麼叫二次剩餘,其實就是對於給定的p(p∈P)和n,如果有x滿足x2≡n(modp),那麼n在模p意義下就是二次剩餘。其實就是模意義下能否開根號。 我們先定義Fp,這是一個數域,其實就是0到p−1這p
DZY Loves Fibonacci Numbers CodeForces - 446C (二次剩餘+線段樹維護等比數列)
二次剩餘: 斐波那契通項公式: 先打表求出根號5在模1e9+9意義下的數。 然後就化簡成立區間加上等比數列的形式,維護每段區間加了多少次等比數列就行。 下面我們來看如何維護一個等比數列。假如我對區間[L,R]的加上1,2,4,8...2^n
BZOJ5104 Fib數列(二次剩餘+BSGS)
5在1e9+9下有二次剩餘,那麼fib的通項公式就有用了。 已知Fn,求n。注意到[(1+√5)/2]·[(1-√5)/2]=-1,於是換元,設t=[(1+√5)/2]n,原式變為√5·Fn=t-(-1)n·t-1。同乘t並移項,可得t2-√5·Fn·t-(-1)n=0。討論n的奇偶性,BSGS求二
基於ArcGIS 二次開發 使用技巧總結
這兩天剛忙完一個專案,趁著這幾天任務輕鬆,抽空總結上一個專案所遇到的一些問題,都是很簡單的基本操作,先列個大綱吧: 一、地圖的基本操作:(傳送門:https://blog.csdn.net/KK_bluebule/article/details/83414871) 1.工具欄的實現:
無約束演算法-最速下降,牛頓法,擬牛頓,共軛梯度求解二次函式極小值
import numpy as np import math a=np.random.randint(1,10,size=[100,1]) G=(a*a.T)+np.random.randint(1,5)*np.eye(100) b=np.dot(G,np.ones(
2018.12.19【Timus1132】Square Root(模奇質數二次剩餘)(Cipolla)
傳送門 解析: 這道題由於模數一定是質數,所以我們只需要特判掉模數為2的情況,剩下的就是模奇質數二次剩餘了。 關於二次剩餘可以看我的部落格 程式碼: #include<bits/stdc++.h> using namespace std; #d
python求解二次規劃問題
Python中支援Convex Optimization(凸規劃)的模組為CVXOPT,其安裝方式為: pip install cvxopt 一、數學基礎 二次型 二次型(quadratic for
N次剩餘和二次剩餘
N次剩餘 給定 \(N,a,P\),且 \(P\) 最好為質數 可以算出 \(x^N\equiv a(mod~p)\) 的解 首先可以算出 \(P\) 的原根 \(g\) 解方程 \(g^y\equiv b(mod~p)\),這個直接 \(BSGS\) 設 \(g^z\equiv x(mod~p)\) 那麼
2018.12.30【NOIP訓練】【SCOI2018】Numazu 的蜜柑(二次剩餘)
題面傳送門 解析: 直接解方程可以得到 a u
【模板】二次剩餘Cipolla演算法/尤拉準則-bzoj5104: Fib數列
尤拉準則 對於質數 p p p,
hdu 3589 Jacobi symbol (二次剩餘勒讓德符號)
題目連結 題意:交代一下勒讓德符號與二次剩餘,然後告訴你J(a,n)與L的關係,給定a,n,求J(a,n)。 二次剩餘的原理我並沒有搞太懂= =,想著畢竟不常見,會用板子就好了。在知道如何求勒讓德符號的情況下,只需要將n分解質因數,假設n=p1^k1 * p2^k2 *
BZOJ 5104 Fib數列(二次剩餘+BSGS)
斐波那契數列的通項: \[\frac{1}{\sqrt{5}}((\frac{1+\sqrt{5}}{2})-(\frac{1-\sqrt{5}}{2}))\] 設T=\(\sqrt{5}*N\),\(y=\frac{\sqrt{5}+1}{2}\) 原式可化為\(y^n-(-\frac{1}{y}^n) \
求解二次同餘式
求解形如 x^2 = a (mod p) 這樣的同餘式 /* 模P平方根: 求 X ^2 = a (mod p) 定理:當P為!!!奇素數 !!!的時候 先判斷(a / p )的勒讓德符號, 若為-1則無解,若為1則有解 分解P-1,然後求B
Timus 1132 Square Root(二次剩餘)
#include<cstdio> #include<cstdlib> #include<algorithm> using namespace std; typedef long long LL; int w; struct T {
Timus 1132 Square Root(二次剩餘 解法2)
#include<cstdio> using namespace std; int Pow(int a,int b,int p) { int res=1; for(;b;a=1LL*a*a%p,b>>=1) if(b&1)