大致題意：給你一個仙人掌圖，讓你計算：。

根據去年多校賽某一道題的經驗，很多仙人掌圖的問題，其實可以轉化為樹的問題。所以我們同樣考慮，如果這是一棵樹的話如何去做。注意到表示式裡面的flow(i,j)表示從i到j的最小割或最大流，而在樹上的最小割可以看作是兩點之間連線的最短邊，那麼我們要做的就是統計每一條邊作為最短邊的貢獻。這樣我們不禁就聯想到了之前做過的 Codeforces 915F 。這題是求任意兩點之間路徑上最長邊減去最短邊之差之和。

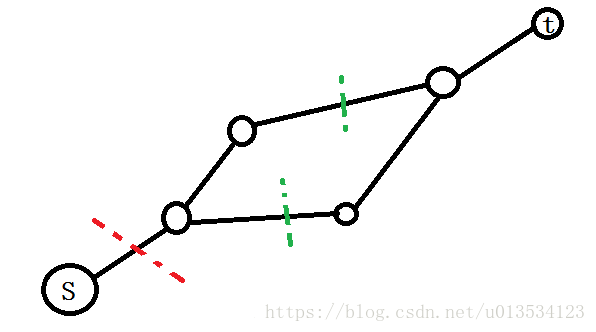
和那題類似，在不考慮仙人掌圖，而是普通樹的情況下，本題考慮對邊進行排序，然後不斷的並查集合並統計每條邊產生的新貢獻。那麼我們現在考慮，當不是樹的時候，根據仙人掌圖的定義，每個點最多隻能在一個簡單環內部。我們考慮包含這樣一個環的路徑的最小割，這樣的最小割，要麼是普通路徑上的一條邊，要麼是環中的最短邊加上另一條邊。具體可以參見下圖：

我們要麼切掉類似紅色的邊，要麼切掉兩條類似兩條綠色的邊，然後可以證明兩個綠色的邊一定會有一條環中流量最小的邊。既然如此，如果我們找到這條邊，然後把這個權值加入到環中的其他邊中，然後刪掉這條邊，再求最小割對最後結果也不會產生影響。所以我們不妨把所有的環都這麼處理，這樣一個仙人掌圖就會變成一棵樹，我們也就可以按照之前所說的那麼做了。

具體來說，如果找到這個最小的邊呢。我們不妨做一遍最大生成樹，這樣剩下的邊就一定能夠與某些點構成環，而且一定是這些環中的邊裡面流量最小的。然後我們dfs求出fa和dep等資訊，然後遍歷環中的邊，把每條邊的權值加上這個最小流量。之後就用這個新的樹新的邊求解。本題需要考慮的是路徑中的最小值，所以我們邊也是一樣從最大的開始合併。每次並查集合並，然後計算貢獻。

這個貢獻，由於又要考慮上兩個端點i和j，所以還要有一些技巧。具體來說於 Codeforces 724G 有點類似。分別統計每一個連通塊裡面有多少個數在對應二進位制位的值是1和0的個數。合併的時候一起合併即可。還有，最後答案比較坑，需要用到ull。具體見程式碼：

#include<bits/stdc++.h>
#define N 200010
#define LL long long
#define IO ios::sync_with_stdio(0);cin.tie(0)
using namespace std;

struct edge
{
    int x,y,w;

    bool operator < (const edge a) const
    {
        return w>a.w;
    }

} e[N];

int n,m,f[N],fa[N],dep[N],pre[N];
int cnt[N][32][2],sz[N][32][2];
struct Edge{int y,w;};
vector<Edge> g[N];
vector<edge> G;

int find(int x)
{
    return f[x]==x?x:f[x]=find(f[x]);
}

void dfs(int x,int ff,int d)
{
    fa[x]=ff; dep[x]=d;
    for(int i=0;i<g[x].size();i++)
    {
        int y=g[x][i].y;
        if (y==ff) continue;
        dfs(y,x,d+1); pre[y]=i;
    }
}

void init()
{
    for(int i=1;i<N;i++)
        for(int j=0;j<31;j++)
        {
            cnt[i][j][0]=(i>>j)&1^1;
            cnt[i][j][1]=(i>>j)&1;
        }
}

int main()
{
    IO; int T;
    cin>>T; init();
    while(T--)
    {
        cin>>n>>m;
        G.clear();
        for(int i=1;i<=n;i++)
        {
            f[i]=i,g[i].clear();
            for(int j=0;j<31;j++)
            {
                sz[i][j][0]=cnt[i][j][0];
                sz[i][j][1]=cnt[i][j][1];
            }
        }
        for(int i=1;i<=m;i++)
            cin>>e[i].x>>e[i].y>>e[i].w;
        sort(e+1,e+1+m);
                                                    //kruskal
        for(int i=1;i<=m;i++)
        {
            int x=e[i].x,y=e[i].y,w=e[i].w;
            if (find(x)!=find(y))
            {
                f[find(x)]=find(y);
                g[x].push_back(Edge{y,w});
                g[y].push_back(Edge{x,w});
            } else G.push_back(edge{x,y,w});
        }
                                                    //get fa[] & pre[] & dep[]
        dfs(1,0,0);
                                                    //delete the minimum edge in the circle
        for(int i=0;i<G.size();i++)
        {
            int x=G[i].x,y=G[i].y,w=G[i].w;
            if (dep[x]<dep[y]) swap(x,y);
            for(;dep[x]>dep[y];x=fa[x])
                g[fa[x]][pre[x]].w+=w;
            for(;x!=y;x=fa[x],y=fa[y])
            {
                g[fa[x]][pre[x]].w+=w;
                g[fa[y]][pre[y]].w+=w;
            }
        }
                                                    //rebuild the graph and sort
        int tot=0;
        for(int i=1;i<=n;i++)
            for(int j=0;j<g[i].size();j++)
                if (dep[g[i][j].y]>dep[i])
                    e[++tot]=edge{i,g[i][j].y,g[i][j].w};
        sort(e+1,e+1+tot);
                                                    //initial dsu
        for(int i=1;i<=n;i++) f[i]=i;
                                                    //calculate the answer
        unsigned long long ans=0;
        for(int i=1;i<=tot;i++)
        {
            int x=e[i].x,y=e[i].y,w=e[i].w;
            x=find(x); y=find(y); f[x]=y;
            for(int j=0;j<31;j++)
            {
                if ((w&(1LL<<j))) ans+=(1LL*sz[x][j][0]*sz[y][j][0]+1LL*sz[x][j][1]*sz[y][j][1])*(1LL<<j);
                             else ans+=(1LL*sz[x][j][0]*sz[y][j][1]+1LL*sz[x][j][1]*sz[y][j][0])*(1LL<<j);
                sz[y][j][0]+=sz[x][j][0]; sz[y][j][1]+=sz[x][j][1];
            }
        }

        cout<<ans<<endl;
    }
    return 0;
}