機器學習練習二:多元線性迴歸
<div class="markdown_views"><hr>
這篇文章是一系列 Andrew Ng 在 Coursera 上的機器學習課程的練習的一部分。這篇文章的原始程式碼,練習文字,資料檔案可從這裡獲得。
在 我的機器學習系列文章的第一部分,我們完成了 Andrew Ng 的 Machine Learning 練習 1 的第一部分。在本篇文章中,我們將完成 練習 1 的第 2 部分以結束整個 練習 1。如果你還記得,在第一部分,我們實現了線性迴歸以預測基於城市人口的食品卡車要放在哪裡。在第二部分,我們有了新任務——預測房子的銷售價格。這次的不同之處是我們有多個因變數——如:房子的平方英尺數和房子裡的臥室數。我們能迅速的拓展我們之前的程式碼來處理多元線性迴歸嗎?
讓我們找出來吧!
首先,讓我們看一看資料。
path = os.getcwd() + '\data\ex1data2.txt'
data2 = pd.read_csv(path, header=None, names=['Size', 'Bedrooms', 'Price'])
data2.head() - 1
- 2
- 3

- 1
- 2
- 3
| Size | Bedrooms | Price | |
|---|---|---|---|
| 0 | 2104 | 3 | 399900 |
| 1 | 1600 | 3 | 329900 |
| 2 | 2400 | 3 | 369000 |
| 3 | 1416 | 2 | 232000 |
| 4 | 3000 | 4 | 539900 |
注意,每個變數的數值規模是截然不同的。一個房子通常有 2-5 間臥室但可能面積有從幾百到幾千平方英尺的。如果我們就這樣的在這些資料上運用我們的迴歸
data2 = (data2 - data2.mean()) / data2.std()
data2.head() - 1
- 2

- 1
- 2
| Size | Bedrooms | Price | |
|---|---|---|---|
| 0 | 0.130010 | -0.223675 | 0.475747 |
| 1 | -0.504190 | -0.223675 | -0.084074 |
| 2 | 0.502476 | -0.223675 | 0.228626 |
| 3 | -0.735723 | -1.537767 | -0.867025 |
| 4 | 1.257476 | 1.090417 | 1.595389 |
接下來,我們需要修改在第一部分中的線性迴歸實現以處理多個自變數。我們真的需要嗎?讓我們再次看看梯度下降的程式碼。
defgradientDescent(X, y, theta, alpha, iters):
temp = np.matrix(np.zeros(theta.shape))
parameters = int(theta.ravel().shape[1])
cost = np.zeros(iters)
for i in range(iters):
error = (X * theta.T) - y
for j in range(parameters):
term = np.multiply(error, X[:,j])
temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))
theta = temp
cost[i] = computeCost(X, y, theta)
return theta, cost- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
仔細看計算誤差項的那行程式碼:error = (X * theta.T) - y。起初可能並不明顯,但我們正在使用矩陣運算!這就是線性代數的力量。這段程式碼將會正確的執行不管多少變數(列)屬於 X 的行數一致。最重要的是,它是一個非常高效的計算。這是一個強大的方法一下將任何表示式應用到大量的例項中。
既然我們的梯度下降和代價函式用的都是矩陣運算,事實上沒有改變程式碼來處理多元線性迴歸的必要。讓我們來試一試。我們首先需要執行一些初始化來建立合適的矩陣以傳遞給我們的函式。
# add ones column
data2.insert(0, 'Ones', 1)
# set X (training data) and y (target variable)
cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
y2 = data2.iloc[:,cols-1:cols]
# convert to matrices and initialize theta
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
theta2 = np.matrix(np.array([0,0,0])) - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
現在,我們已經準備好試一試了。讓我們看看會怎麼樣。
# perform linear regression on the data set
g2, cost2 = gradientDescent(X2, y2, theta2, alpha, iters)
# get the cost (error) of the model
computeCost(X2, y2, g2) - 1
- 2
- 3
- 4
- 5

- 1
- 2
- 3
- 4
- 5
0.13070336960771897- 1

- 1
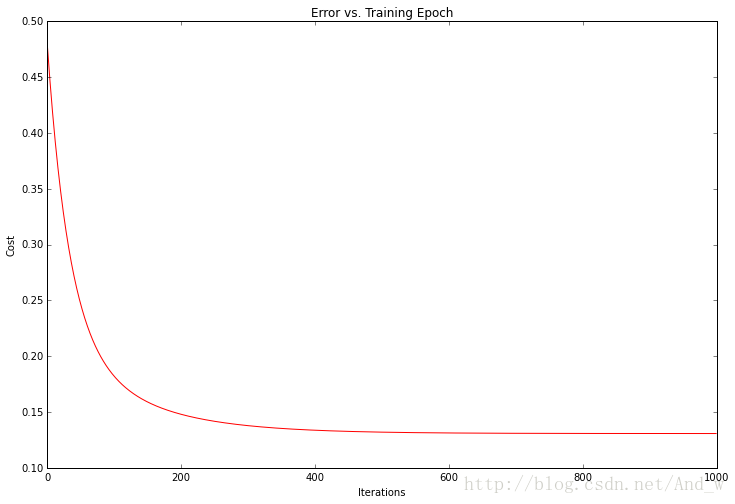
看起來不錯!我們也可以繪製訓練過程以確認每次梯度下降迭代後誤差事實上都在下降。
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost2, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch') - 1
- 2
- 3
- 4
- 5

- 1
- 2
- 3
- 4
- 5
代價函式或者解的誤差,在每次成功的迭代後都下降了直到觸底。這正是我們所期待的。這看起來像我們的演算法執行正常。
值得注意的是,我們不必從頭開始實現任何演算法來解決這個問題。
Python 的一個好處是,它有龐大的開發者社群和大量的開源軟體。在機器學習領域,頂尖的 Python 庫是 scikit-learn 。讓我們看看怎麼用 scikit-learn 的線性迴歸類處理我們第一部分的簡單線性迴歸任務。
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X, y) - 1
- 2
- 3

- 1
- 2
- 3
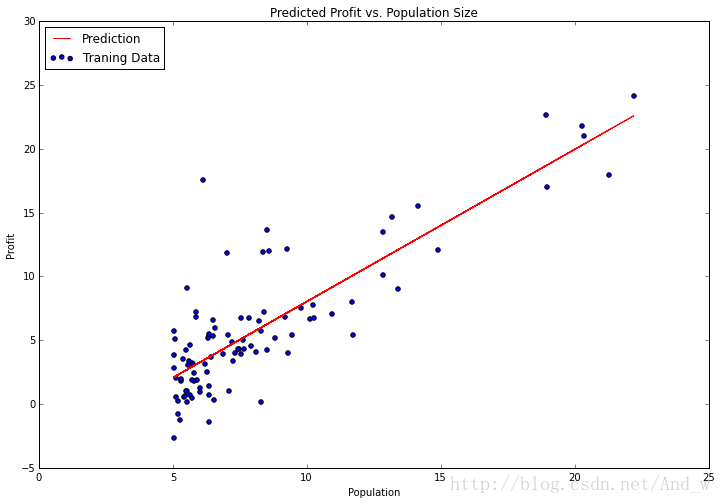
沒有什麼比這個更容易了。fit 方法有很多引數供我們調整,這取決於我們想要的演算法功能,對於我們的問題預設的已經足夠了,所以我留下了他們。讓我們試著繪製擬合引數( the fitted parameters)看看和我們之前的解有何差別。
x = np.array(X[:, 1].A1)
f = model.predict(X).flatten()
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size') - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
注意:為了畫出這條線,我使用了 predict 函式來獲取預測的 y 值。這比試圖手動設定更容易。Scikit-learn 有十分優秀的 API 對典型的機器學習工作流提供很多便捷的函式。在以後的文章裡我們將更仔細地研究其中的一些。
今天就這麼多。在第三部分,我們將看看 練習 2 並且用邏輯迴歸的方法進行一些分類任務。
相關推薦
機器學習練習二:多元線性迴歸
<div class="markdown_views"><hr> 這篇文章是一系列 Andrew Ng 在 Coursera 上的機器學習課程的練習的一部分。這篇文章的原始程式碼,練習文字,資料檔案可從這裡獲得。
吳恩達機器學習(二)多元線性迴歸(假設、代價、梯度、特徵縮放、多項式)
目錄 0. 前言 學習完吳恩達老師機器學習課程的多變數線性迴歸,簡單的做個筆記。文中部分描述屬於個人消化後的理解,僅供參考。 0. 前言 多元線性迴歸(Multivari
機器學習(4)-多元線性迴歸
一個唯一的因變數和多個自變數 之間的關係 這裡自變數在處理之前不僅僅是數值型 上圖: 我們要做的也就是,尋找到最佳的b0、b1、…….bn 這裡有關於50個公司的資料: spend1、2、3代表了公司在某三個方面的花銷,state是公司的的地址
吳恩達機器學習練習1——單變數線性迴歸
機器學習練習1——單變數線性迴歸代價函式:梯度下降練習1資料集代價函式梯度下降法視覺化J 單變數線性迴歸 代價函式: 梯度下降 練習1 資料集 X代表poplation,y代表profits 資料集的視覺化 function plotData(x,
機器學習公開課筆記(2):多元線性迴歸
多元線性迴歸 一元線性迴歸只有一個特徵$x$,而多元線性迴歸可以有多個特徵$x_1, x_2, \ldots, x_n$ 假設 (Hypothesis):$h_\theta(x)=\theta^Tx=\theta_0x_0+\theta_1x_1+\ldots+\theta_nx_n$ 引數 (Para
機器學習(二):理解線性迴歸與梯度下降並做簡單預測
# 預測從瞎猜開始 按[上一篇文章](https://mp.weixin.qq.com/s/-KsbtgOc3C3ry-8P5f8K-Q)所說,機器學習是應用數學方法在資料中發現規律的過程。既然數學是對現實世界的解釋,那麼我們迴歸現實世界,做一些對照的想象。 想象我們面前有一塊塑料泡沫做的白板,白板上
【機器學習演算法推導】簡單線性迴歸與多元線性迴歸
線性迴歸,主要用於從資料中擬合出一條直線(或更高維的平面),這條直線能夠很好地體現資料的特徵,比如,它能夠使得平面上的點都均勻地分佈在這條直線上。 演算法思想 對於簡單線性迴歸和多元線性迴歸,其演算法過程是相同的,不同之處在於簡單線性迴歸只有一個特徵需要擬合,多元線
機器學習七--回歸--多元線性回歸Multiple Linear Regression
clas http span str 圖片 style port import num 一、不包含分類型變量 from numpy import genfromtxtimport numpy as npfrom sklearn import datasets,linear
機器學習之路: python線性回歸 過擬合 L1與L2正則化
擬合 python sco bsp orm AS score 未知數 spa git:https://github.com/linyi0604/MachineLearning 正則化: 提高模型在未知數據上的泛化能力 避免參數過擬合正則化常用的方法: 在目
機器學習實戰(七)線性迴歸(Linear Regression)
目錄 0. 前言 1. 假設函式(Hypothesis) 2. 標準線性迴歸 2.1. 代價函式(Cost Function) 2.2. 梯度下降(Gradient Descent) 2.3. 特徵縮放(Feat
Bobo老師機器學習筆記第五課-線性迴歸演算法的評估指標
評價線性迴歸的指標有四種,均方誤差(Mean Squared Error)、均方根誤差(Root Mean Squared Error)、平均絕對值誤差(Mean Absolute Error)以及R Squared方法。 sklearnz中使用的,也是大家推薦的方法是R Squared方法。
機器學習筆記(一)線性迴歸模型
一、線性迴歸模型 (一)引入—梯度下降演算法 1. 線性假設: 2. 方差代價函式: 3. 梯度下降: 4. : learning rate (用來控制我們在梯度下降時邁出多大的步子,值較大,梯度下降就很迅速) 值過大易造成無法收斂到minimum(每一步邁更大)
Python金融系列第五篇:多元線性迴歸和殘差分析
作者:chen_h 微訊號 & QQ:862251340 微信公眾號:coderpai 第一篇:計算股票回報率,均值和方差 第二篇:簡單線性迴歸 第三篇:隨機變數和分佈 第四篇:置信區間和假設檢驗 第五篇:多元線性迴歸和殘差分析 第六篇:現代投資組合
虛擬機器學習之二:垃圾收集器和記憶體分配策略
1.物件是否可回收 1.1引用計數演算法 引用計數演算法:給物件中新增一個引用計數器,每當有一個地方引用它時,計數器值就加1;當引用失效時,計數器值就減1;任何時候計數器值為0的物件就是不可能再被使用的物件。 客觀來說,引用計數演算法的實現簡單,判定效率高,在大部分情況下都是
機器學習100天---day02 簡單線性迴歸模型
資料集: Hours,Scores 2.5,21 5.1,47 3.2,27 8.5,75 3.5,30 1.5,20 9.2,88 5.5,60
機器學習之二:決策樹
本文為作者學習K近鄰演算法後的整理筆記,僅供學習使用! 決策樹 1、概述 決策樹(Decision Tree)實在已知各種情況發生概率的基礎上,通過構成決策樹來求取淨現值的期望值大於等於0的概率,評價專案風險,判斷其可行性的決策分析方法,是直觀運用概率分析的一種圖
機器學習經典演算法總結 一.線性迴歸
一.基本形式 hθ(x)=θ0+θ1x1+θ2x2+....+θnxn=θTxh_θ(x)=θ_0+θ_1x_1+θ_2x_2+....+θ_nx_n=θ^Txhθ(x)=θ0+θ1x1+θ2x2+....+θnxn=θTx 二.損失函式 最常用
吳恩達機器學習(第二章)----線性迴歸
線性迴歸要做的主要包含代價函式和梯度下降。 一、基本解釋 線性迴歸的過程其實就是我們在選擇好某個型別的函式之後去不斷的擬合現有的資料,那麼什麼情況下我們這個函式是最符合,最貼近我們這些資料的呢?就是在代價函式的值最小的時候。 二、代價函式 假設要擬合的函式是h(x)=
#機器學習筆記01#多變數線性迴歸
1多變數線性迴歸 1.1 回顧單變數線性迴歸 訓練集提出: Training set of housing prise 以房屋價格為例 Size in feet(x) Price in 1000’s (y) 2104 460 1416 2
機器學習筆記五:廣義線性模型(GLM)
一.指數分佈族 在前面的筆記四里面,線性迴歸的模型中,我們有,而在logistic迴歸的模型裡面,有。事實上,這兩個分佈都是指數分佈族中的兩個特殊的模型。所以,接下來會仔細討論一下指數分佈族的一些特點,會證明上面兩個分佈為什麼是指數分佈族的特性情況以及怎麼用到