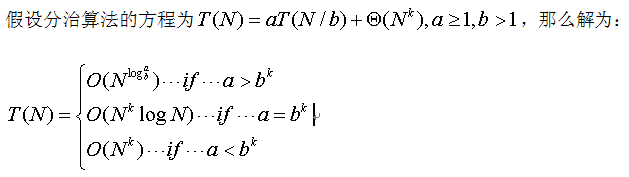分治演算法(divide and conquer)
0) 引論
正如名字divide and conquer所言,分治演算法分為兩步,一步是divide,一步是conquer。
Divide:Smaller Problems are solved recursively except base cases.
Conquer:The solution to the original problem is then formed from the solutions to the sub-problem.
說白了,分治演算法就是把一個大的問題分為若干個子問題,然後在子問題繼續向下分,一直到base cases,通過base cases的解決,一步步向上,最終解決最初的大問題。分治演算法是遞迴的典型應用。
1) 分治排序的執行時間問題
這裡寫下這個結論只是為了後面分析時間問題的方便。
2) 最近點問題
假設在座標平面上分佈了一系列的點,那麼問題是求取這些點兩兩之間的最短距離。
最naive的做法當然是窮舉法,計算所有的兩兩點間的距離,然後取最小值。窮舉法對於小樣本總是不錯的。但是對於大樣本來說,就不是那麼合適了,這裡我們用divide-and-conquer演算法來解決這一問題。
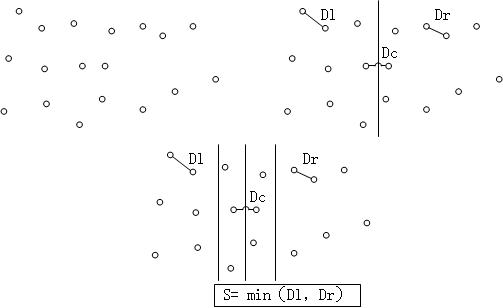
首先對於所有的點,按照x座標將其分為兩部分,這就是divide,那麼最短距離就是左邊部分中的最短距離Dl,右邊部分的最短距離Dr,以及左右部分之間的距離Dc。對於Dl以及Dr,可以遞迴的計算得到,這就是conquer。那麼唯一的問題就是Dc。我們知道如果最短距離是Dc的話,那麼Dc<=min(Dl,Dr)。因此我們只需要計算距離divide分割線S = min(Dl,Dr)的點就可以了。進一步我們可以看到對於每個在2S區域內的點,只需要計算y座標距離這一點不大於S的點就可以,這樣可以進一步簡化運算量。
for(i=0;i<NumPointsInStrip;i++)
for(j=i+1;j<NumPointsInStrip;j++)
if(Pi and Pj coordinates differ by more than S)
break;
else
if(Dist(Pi,Pj)<S)
S = Dist(Pi,Pj);相關推薦
分治演算法(divide and conquer)
0) 引論 正如名字divide and conquer所言,分治演算法分為兩步,一步是divide,一步是conquer。 Divide:Smaller Problems are solved recursively except base cases. Conquer:
【3】分治法(divide-and-conquer)
分治法 顧名思義,分治法是將一塊完整的領土分解為若干小的領土,然後一塊塊征服。 分,把一個問題的例項劃分為若干個子問題(原問題規模變小) 治,遞迴地解決每個子問題 把每一個子問題的解整合為一個大問題的解 舉例 歸併排序(Merge sort) 將待排序的
2.1 493. Reverse Pairs (Divide and Conquer)
題目: Given an array nums, we call (i, j) an important reverse pair if i < j and nums[i] > 2*nums[j]. You need to return the num
327. Count of Range Sum(Divide and Conquer)
題目: Given an integer array nums, return the number of range sums that lie in [lower, upper] inclusive. Range sum S(i, j) is defined as
幾個精妙的小問題(By Divide and Conquer)
所謂分治法就是分而治之的意思,即將一個不易解決的大問題分解為幾個易於解決的小問題,然後再將各個小問題的解合併起來就是大問題的解。這種方法雖然簡單,但是對於很多問題都很有效,下面試舉幾例: 問題一:有效字串個數問題能在通道上傳遞的字串滿足如下兩條性質:該字串中只包含'a'、
分而治之(divide and conquer,D&C)
分而治之並不是一種演算法,而是一種解決演算法的思想(一種遞迴的演算法)。分而治之單充的理解起來可能有些困難,下面大概的解釋一下:有一個這樣的需求,我有一個長方形,需要分割成均勻的正方形,而且分割成的正方形要儘可能的大。大家可以想一下如何實現這個問題?(思考十幾秒)下面我們用D
STL之劃分與排序演算法(Partions and Sorting)
目錄 STL之劃分與排序演算法(Partions and Sorting) 劃分演算法 一、is_partitoned 二、partition 三、partition_copy(beg,
演算法設計與分析(二):Divide And Conquer
Maximum Subarray Given an integer array nums, find the contiguous subarray (containing at least one number) which has the larges
ADA演算法知識(七)Divide and conquer algorithm(分治法解決最大子陣列和問題)
[Maximum Subarry Sum] The maximum subarry sum problem takes as input an array of (positive or negative) integers a[1..n] and returns the largest sum o
ADA演算法知識(四)Divide-and-conquer algorithm
分治演算法 Divide the problem into smaller sub-problems. Governance - breaking down these smaller sub-problems one by one; Combination - merge the solved
演算法設計與分析(一):Divide And Conquer
Search a 2D Matrix II Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following pro
【Divide and Conquer】169. Majority Element(easy)
比較 esc time ble nbsp 也有 assume ray more #Week_1# #From LeetCode# Description: Given an array of size n, find the majority element.
【LeetCode】分治法 divide and conquer (共17題)
p.p1 { margin: 0.0px 0.0px 0.0px 0.0px; font: 12.0px Helvetica } 【4】Median of Two Sorted Arrays 【23】Merge k Sorted Lists 【53】Maximum Subarra
樹及其衍生演算法(Trees and tree algorithms)
1,二叉樹(Binary tree) 二叉樹:每一個節點最多兩個子節點,如下圖所示: 相關概念:節點Node,路徑path,根節點root,邊edge,子節點 children,父節點parent,兄弟節點sibling, 子樹subtree,葉子節點leaf node,
圖及其衍生演算法(Graphs and graph algorithms)
1. 圖的相關概念 樹是一種的圖,相比樹,圖更能用來表示現實世界中的的實體,如路線圖,網路節點圖,課程體系圖等,一旦能用圖來描述實體,能模擬和解決一些非常複雜的任務。圖的相關概念和詞彙如下: 頂點vertex:圖的節點 邊Edge:頂點間的連線,若邊具有方向時,組成有向圖
演算法課7-Divide and Conquer
分治的思想,最經典的兩個例子首先是排序的兩個例子 一個是快排 一個是歸併排序【請看到這裡的你,去複習一下排序演算法】 快速排序 先總體再區域性 int partition(int nums[],in
[LeetCode][演算法初級][字串]39 數數並說 (count and say)
題目挺奇怪的,看了一會才知道是什麼意思。。就是讓你去數一個字串的數字,並且把你說出來的內容作為下一個字串繼續數。比如:第一個字串是“1”,你就要數:"1個1!",同時寫下”11“作為下一個字串。然後你再數”2個1!“同時寫下”21“. 然後再數”1個2,1個1 !“,那麼下一
分治演算法(歸併排序、一維點對、HDU-1007)
分治演算法的基本思想是將一個規模為N的問題分解為K個規模較小的子問題,這些子問題相互獨立且與原問題性質相同。求出子問題的解,就可得到原問題的解。 分治法解題的一般步驟: 分解,將要解決的問題劃分成若干規模較小的同類問題; 求解,當子問題劃分得足夠小時,
【C++實現】五大常用演算法之一:分治演算法(例項:漢諾塔)
求解思想:大而化小 1、問題拆分成子問題 2、對子問題求解 在漢諾塔遊戲中,有三個分別命名為A、B、C得塔座,幾個大小各不相同,從小到大一次編號得圓盤,每個原盤中間有一個小孔。最初,所有得圓盤都在A塔座上,其中最大得圓盤在最下面,然後是第二大,以此類推. 先上程式
五大常用演算法之一:分治演算法(轉)
分治演算法 一、基本概念 在電腦科學中,分治法是一種很重要的演算法。字面上的解釋是“分而治之”,就是把一個複雜的問題分成兩個或更多的相同或相似的子問題,再把子問題分成更小的子問題……直到最後子問題可以簡單的直接求解,原問題的解即子問題的解的合併。這個技巧是很多高效演算法的基礎,如排序演算法(快速排序,