最長公共子序列是動態規劃基本題目，下面按照動態規劃基本步驟解出來。

1.找出最優解的性質，並刻劃其結構特徵

序列a共有m個元素，序列b共有n個元素，如果a[m-1]==b[n-1]，那麼a[:m]和b[:n]的最長公共子序列長度就是a[:m-1]和b[:n-1]的最長公共子序列長度+1；如果a[m-1]!=b[n-1]，那麼a[:m]和b[:n]的最長公共子序列長度就是MAX（a[:m-1]和b[:n]的最長公共子序列長度，a[:m]和b[:n-1]的最長公共子序列長度）。

2.遞迴定義最優值

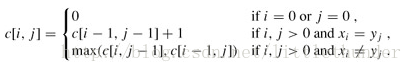
3.以自底向上大方式計算出最優值

python程式碼如下：

def lcs(a,b):
	lena=len(a)
	lenb=len(b)
	c=[[0 for i in range(lenb+1)] for j in range(lena+1)]
	flag=[[0 for i in range(lenb+1)] for j in range(lena+1)]
	for i in range(lena):
		for j in range(lenb):
			if a[i]==b[j]:
				c[i+1][j+1]=c[i][j]+1
				flag[i+1][j+1]='ok'
			elif c[i+1][j]>c[i][j+1]:
				c[i+1][j+1]=c[i+1][j]
				flag[i+1][j+1]='left'
			else:
				c[i+1][j+1]=c[i][j+1]
				flag[i+1][j+1]='up'
	return c,flag

def printLcs(flag,a,i,j):
	if i==0 or j==0:
		return
	if flag[i][j]=='ok':
		printLcs(flag,a,i-1,j-1)
		print(a[i-1],end='')
	elif flag[i][j]=='left':
		printLcs(flag,a,i,j-1)
	else:
		printLcs(flag,a,i-1,j)
		
a='ABCBDAB'
b='BDCABA'
c,flag=lcs(a,b)
for i in c:
	print(i)
print('')
for j in flag:
	print(j)
print('')
printLcs(flag,a,len(a),len(b))
print('')
 

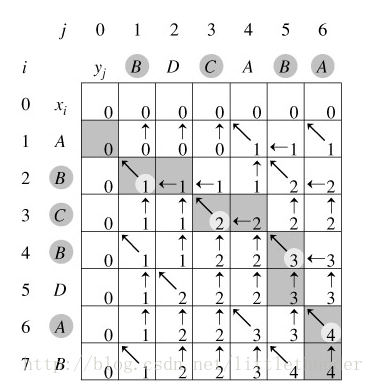
執行結果輸出如下：

4.根據計算最優值得到的資訊，構造最優解

上圖是執行結果，第一個矩陣是計算公共子序列長度的，可以看到最長是4；第二個矩陣是構造這個最優解用的；最後輸出一個最優解BCBA。