在數據挖掘過程中，當一個對象有多個屬性（即該對象的測量過程產生多個變量）時，會產生高維度數據，這給數據挖掘工作帶來了難度，我們希望用較少的變量來描述數據的絕大多數信息，此時一個比較好的方法是先對數據進行降維處理。數據降維過程不是簡單提取部分變量進行分析，這樣的方式法當然會降低數據維度，但是這是非常不可取的方式（不專業一點，可以稱之為“丟維”），違背了“降維”的含義。

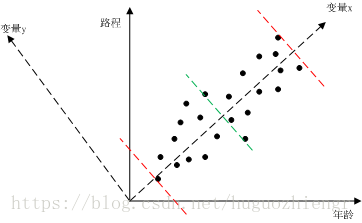
盡管我們並不確定不同變量之間是否一定有關系，但除非有確定的依據，我們最好還是猜測是有關系的，先看一個簡單的例子，只有兩個變量的情況。我們對人的年齡和他當前所走過的路程進行統計，然後繪制成圖1（此處的例子是自己想的，不太妥當，只為說明問題）

?

圖1

在圖1中，我們對所有的樣點進行一元線性回歸分析，可以得到變量x直線，將變量x直線逆時針旋轉90度，得到變量y直線（得到我們熟悉的二維直角坐標系），我們可以直觀的看到樣本數據主要沿著變量x分布，那麽在數學上怎麽去判別這種“直觀的分布”呢？我們用最大方差來判別。圖1中兩條紅色虛線是樣本沿變量x的分布範圍，綠色虛線是樣本數據在變量x這一維度上的均值，這樣我們就可以求得樣本數據在變量x維度上的方差，類似的，可以求得樣本數據在變量y上的方差，很明顯，樣本數據在變量x維度上的方差較大。

那麽方差大說明什麽問題呢？方差大說明樣本數據在該維度上包含更多的信息。我們可以這樣想，如果樣本數據在某個維度上基本不變化，那麽說明這個維度代表的變量的有、無對數據分布沒有影響，該變量就沒有存在的必要了，在測量過程中，我們就不必測量對象的這個屬性。所以，此時可以用變量x這樣一個變量來描述對象的年齡、路程屬性。

這裏還有兩個問題需要說明，一個是變量x代表什麽含義，另外一個就是在多維數據降維過程中，什麽樣的變量（類似於變量x這種）才是符合我們要求的變量。在我碼這些字的時候，我也沒弄明白問題一，所以先跳過，後面弄明白了再來補充。對於問題二，在降維之後，我們會得到一系列的新的維度，以及這些維度所代表的變量，按照樣本數據在這些維度上的投影所得數據的方差大小，對這些新的變量進行排列。假設我們選擇前n個新的變量（假設有的話）,這n個新的變量就已經包含了原數據信息的90%，而這個比例也是我們能夠接受的，那麽這前n個變量就是滿足我們需求的。

下面仔細說明降維的過程（為了方便，所有的向量這裏我就不加方向箭頭，只是標黑處理）

1. 假設X是一個 的數據矩陣，行代表實例對象，列代表變量，我們先對每一列數據都去均值化，也即是列中數據都減去該列數據的均值（如果數據矩陣之前沒有做過該處理）。我們關心的實際上是數據的變化情況，數據矩陣中每一個變量中的數值只是對變量的一種表示，表示的是具有變量所表示屬性的不同實例對象間的相互關系（事實上我們可以對表示變量的數值做一系列變換，只要保持該變量的特性不變即可，例如大小、相等、加法、減法等），因此去均值後我們可以拋開測量過程帶來的一些影響。

2. 假設向量a是當X沿其投影時會使方差最大化的 列向量（也即時降維後滿足我們要求的變量多表示的維），現在將數據矩陣X向向量a上投影，得到Xa，這是一個 的投影值列向量，我們對投影值列向量的方差定義為

　　　　　　　　　　 (1)

由於X的均值為0， V即為數據矩陣X的協方差矩陣。

3. 在式（1）中，為了使得方差最大，我們可以對a各元素等比例放大，但是這是沒有什麽意義的，因此我們給a施加一個約束條件 —— a為單位向量，即,通過引入拉格朗日乘子法，我們得到下列最優化問題方程

對a進行求導，得到

這樣就得到我們熟悉的特征值形式

　　　　　　　　　　　　　　 (2)

4. 通過公式（2）我們可以求得一系列特征值 及其對應的特征向量 ,最大特征值對應的特征向量即為第一主成分分量，第二大特征值對應的特征向量即為第二主成分分量，以此類推。得到公式（2）後我們再回頭看公式（1），方差即為，因此當我們選取前 k 個主成分分量來近似數據矩陣X時，可以對接近誤差做如下定義

我們根據需要選取前k個主成分分量，並且使得接近誤差在我們允許的範圍內。

數據降維——主成分分析（PCA）