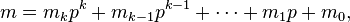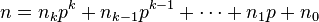Lucas定理 大組合數取模
對於C(n, m) mod p。這裡的n,m,p(p為素數)都很大的情況。就不能再用C(n, m) = C(n - 1,m) + C(n - 1, m - 1)的公式遞推了。
這裡用到Lusac定理
For non-negative integers m and n and a prime p, the following congruence relation holds:
where
and
are the base p expansions of m and n respectively.
對於單獨的C(ni, mi) mod p,已知C(n, m) mod p = n!/(m!(n - m)!) mod p。顯然除法取模,這裡要用到m!(n-m)!的逆元。
根據費馬小定理:
已知(a, p) = 1,則 ap-1 ≡ 1 (mod p), 所以 a*ap-2 ≡ 1 (mod p)。
也就是 (m!(n-m)!)的逆元為 (m!(n-m)!)p-2 ;
程式碼:

typedef long long LL; using namespace std; LL exp_mod(LL a, LL b, LL p) { LL res = 1; while(b != 0) { if(b&1) res = (res * a) % p; a = (a*a) % p; b >>= 1; } return res; } LL Comb(LL a, LL b, LL p) { if(a < b) return 0; if(a == b) return 1; if(b > a - b) b = a - b; LL ans = 1, ca = 1, cb = 1; for(LL i = 0; i < b; ++i) { ca = (ca * (a - i))%p; cb = (cb * (b - i))%p; } ans = (ca*exp_mod(cb, p - 2, p)) % p; return ans; } LL Lucas(int n, int m, int p) { LL ans = 1; while(n&&m&&ans) { ans = (ans*Comb(n%p, m%p, p)) % p; n /= p; m /= p; } return ans; } int main() { Read(); int n, m, p; while(~scanf("%d%d%d", &n, &m, &p)) { printf("%lld\n", Lucas(n, m, p)); } return 0; }

相關推薦
Lucas定理 大組合數取模
對於C(n, m) mod p。這裡的n,m,p(p為素數)都很大的情況。就不能再用C(n, m) = C(n - 1,m) + C(n - 1, m - 1)的公式遞推了。 這裡用到Lusac定理 For non-negative integers m and n and a prime p, the f
Lucas定理——大組合數取模
大組合數取模,求C[n][m]%p 公式:C[n][m]%p == C[n%p][m%p]*C[n/p][m/p]%p 注意,Lucas的要求是n,m<=10^5,如果n,m>=10^5,那麼要求p<=10^5 楊輝三角: f[0][
Lucas定理及組合數取模
引入 楊輝三角 std 數據 組合數取模 有關 ans main include 引入: 組合數C(m,n)表示在m個不同的元素中取出n個元素(不要求有序),產生的方案數。定義式:C(m,n)=m!/(n!*(m-n)!)(並不會使用LaTex QAQ)。 根據題目中對組合
Lucas定理(求組合數取模) 擴充套件Lucas定理(解決模數非質情況)
在比賽時 , 如果遇到CmnCnm的n比較大 , 我們不能通過預處理階乘和逆元來計算 , 而題目又要求對答案取一個質數模的時候 , 我們可以用Lucas定理來簡化計算 Lucas 定理: 定義 : n,m是非負整數,p是素數時 , Lucas(
Lucas定理應用分析——大組合數取模
首先給出Lucas(盧卡斯)定理: 有非負整數A、B,和素數p,A、B寫成p進製為:A=a[n]a[n-1]...a[0],B=b[n]b[n-1]...b[0]。 則組合數C(A,B)與C(a[n],b[n])×C(a[n-1],b[n-1])×...×C
大組合數取模-盧卡斯定理
求左邊的 為: 通過觀察你會發現當且僅當i = t , j = r ,能夠得到的係數,及。 所以,。得證。 -------------------------------------------------------------------------------------------
大組合數取模
考慮C(n,m)%P 情況一:n,m很大,P為素數 處理小範圍的階乘和階乘的逆元 用盧卡斯定理即可。盧卡斯定理: 情況二: 當P= p1∗p2∗p3∗...∗pn 求出[Cmn]分別在[p1,p2,p3,…,pn]模意義下的結果,記為 [m1,m
組合數取模&&Lucas定理題集
pac 假設 次方 href ace 範圍 統一 lucas定理 != 題集鏈接: https://cn.vjudge.net/contest/231988 解題之前請先了解組合數取模和Lucas定理 A : FZU-2020 輸出組合數C(n, m) mod p (
[演算法 18_001] Lucas 定理與大組合數取餘
Lucas 定理 該定理是用來求當 (nm) ( n m
求組合數取模(楊輝三角打表 & 求逆元(擴充套件歐幾里得、費馬小定理、尤拉定理、線性求法) & Lucas)
在acm競賽中,組合數取模的題目還是經常會見到的,所以這是有必要掌握的一個演算法。我本人就因為這個東西而被坑了很多次了= =之前的部落格也都扯過了,就不多說了,下面進入正題。 (1)楊輝三角求組合數 楊輝三角這個東西應該都不陌生,三角的兩邊始終為一,之後向
組合數取模(楊輝三角+Lucas定理+模合數)
/* (1) 1 <= m <= n <= 1000 和 1 <= p <= 10^9 ( p可以是任何數 ) 這個問題比較簡單,組合數的計算可以靠 楊輝
hdu5968(組合數取模Lucas定理)
瞬間移動 Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total Sub
3037 Saving Beans (數論,組合數取模,lucas定理)
也是通過看別人的程式碼才知道這個題應該怎麼做:Lucas定理題目相當於求n個數的和不超過m的方案數。如果和恰好等於m,那麼就等價於方程x1+x2+...+xn = m的解的個數,利用插板法可以得到方案數為:(m+1)*(m+2)...(m+n-1) = C(m+n-1,n-1) = C(m+n-1,m)現在
hdu-3037-組合數取模-Lucas定理
http://acm.hdu.edu.cn/showproblem.php?pid=3037 題意很簡單 求C(n+m,m)%p,P是小於1e5的素數 n,m《1e18 那麼得到
hdu3037 lucas 定理 組合數取模
#include<stdio.h> #include<string> #include<map> #include<vector> #include&l
組合數取模1:盧卡斯定理
模板: #include<iostream> #include<algorithm> #include<cstdio> #define ll long long #define N 100005 using namespace std; int k,n,m
各種逆元求法 組合數取模 comb (組合數 Lucas)
組合數取模(comb) 【問題描述】 計算C(m,n)mod 9901的值 【輸入格式】 從檔案comb.in中輸入資料。 輸入的第一行包含兩個整數,m和n 【輸出格式】 輸出到檔案comb.out中。 輸出一行,一個整數 【樣例輸入】 2
求解組合數取模---拓展歐幾里德和費馬小定理求解逆元
組合數:C(n, m) ; 組合數取模:C(n, m) % mod,mod是一個很大的數。1.公式:2.性質:(1)C(n,m)= C(n,n-m) 其中有C(n, 0) = 1;(2)C(n,m)=C(n-1,m-1)+C(n-1,m)。可以用作遞迴中的
盧卡斯定理Lucas(求大組合數)
貼一份盧卡斯定理模板Lucas定理是用來求 c(n,m) mod p,p為素數的值。//C(n,m)=n!/((n-m)!*m!) //性質1 C(n,m)= C(n,n-m);性質2 C(n,m)=C
hdu3037(盧卡斯定理+組合數取模)
題目 題意:松鼠要過冬,然後要在n棵樹上存不超過m個果子。求有多少種存法。 思路:一共有n棵樹,每棵樹上有xi個果子,問題就可以抽象成x1+x2+....+xn=m這樣一個等式。而且xi是可以為0的