一、拜占庭問題的背景這裡就不再介紹直接說演算法：

下面的這個截圖是從Lamport發表的論文中擷取的：

對於這個演算法需要說明的是：

(1) 在第一輪 將軍會把訊息傳送給所有的副官，第i個副官收到的記為 Vi。如 1(這裡代表的是Attack)

(2) 在第二輪裡面，Li(即第i個副官)會懷疑將軍發來的訊息Vi是對還是錯，於是他會問其餘的副官。這樣他就會得到剩下的(n-2)個副官的值。 i從1到n-1，所以每個副官都會得到剩餘的n-2個副官手裡的Vi。在這一步驟裡，忠誠的副官j會直接將自己的 Vj傳送給其它人。叛徒則會發假訊息。

在n=7,m=2的時候 如果將軍是忠臣的話，那麼在第二輪忠誠的副官確實已經可以判斷出要做的決定

這裡對進入第三輪的解釋是，如L1收到其它L2~L6發來的Vj, 但是他要懷疑準確性，比如L1會想L2發給自己是否是正確的呢？那麼就進入第三輪進行投票。

(3)在第三輪裡面，接著(2)中後面的問題。L1會依次詢問L3,4,5,6 ，問他們上一輪L2給他們發了什麼，然後L1會得到在(2)中 L2->L3, L2->L4,L2->L5, L2->L6的值 這樣再結合自己的L2->L1的值，從這5個裡面用majority函式投出決定得到L2發給自己的訊息值

這樣L1就完成了第二輪的確認。之後L1再從第一步中將軍發給自己的vi和第二輪中確定的5個值中投出自己的決定。

其餘的L2，L3.等等也進行同樣的步驟。

二、好像演算法是挺繞的，如果還是沒清晰的話，直接看下面的過程：

這裡需要注意的是：Lamport提出的容錯的兩個條件

IC1：即所有的忠誠的副官要遵守同一個命令，即達成一致；

IC2：假如將軍是忠誠的，那麼每一個忠誠的副官都應該按照將軍的意思行事。

這裡將軍是叛徒，所以只要滿足IC1條件即可。

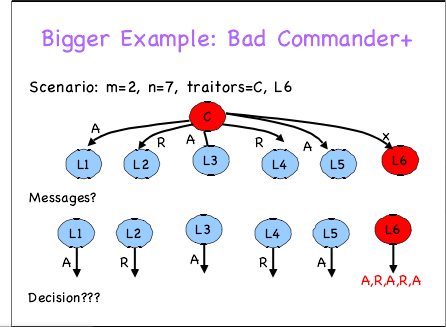
Step1 : C給L1~L6 依次發 A R A R A x  （A，R代表攻擊和撤退，這裡因為C是叛徒，所以可以隨便發給L1-L5訊息，這裡只是一個例子，可以用其他的值，只要最後滿足IC1就可以）

截圖是Step2： 

Step3：其實在第三步中 L1會依次確認在step2中, L2~L6發給自己的資訊. 例如確認L2時 會問L3-L6,在Step2中L2發給你們了什麼

最後得到 R, R, R,X （因為L6這時候肯定又說謊） 再結合自己的R , L1確定在Step2中收到L2發來的是R，之後又確認了L3-L6。大家可以自己在草稿紙上畫出。

其實因為L1-L5都是忠誠，他們不會在Step2中撒謊，所以只需投票L6即可 ，(A R A R A )是L6發給L1-L5的資訊，最後投出發的是A ， 將A修改到step2中L1-L5收到的

資訊中其餘的資訊可以不用改。

最後得到L1-L5均是 4個A， 2個R。 以L1為例=R A  R  A  A  A 

即L1~L5達成了一致。

三、下面來看簽名時候的情形：(詳細的關於簽名的演算法見下一篇部落格)

在lamport的論文中提到：

簽名就是說每次傳送資訊都要簽署上自己的名字，然後再發給別人。而別人只可以在這條訊息上覆制然後再轉發出去。這樣就變的簡單了，

而且

1）忠誠司令的簽名不可偽造，內容修改可以被檢測出來。

2）任何人都可以識別司令的簽名，叛徒可以偽造叛徒司令的簽名。

四、下面來看相關的證明。

證明1： 為什麼在沒有簽名的情況下，n>3m即可容錯？

在Lamport的論文中，在證明OM(m)在最多隻有m個叛徒，以及超過3m個將軍的時候可以滿足IC（1）和IC（2）條件的時候，先引入了一個引理：

證明：（1）當m=0的時候，如果將軍是忠誠的，因為在OM(0)的時候忠臣會遵守將軍發來的命令。而此時的將軍是忠臣的所以，即滿足IC2

      （2）當m>0的時候。用數學歸納法，通過證明OM(m-1)有效來證明。因為假設了n>2k+m,在OM(m-1)時剩餘的將軍數是n-1,但是叛徒數仍然是k(因為上1輪中的將軍是忠臣)，n>2k+m -> n-1>2k+m-1. 又m-1>=0 -> n-1>2k. 即在OM(m-1)中有忠誠的副官比叛徒多，所以可以投票得出正確結果。在O（m-1）時可證。

接著證明“證明1”中的問題：

證明：通過m的歸納法證明，我們通過假設OM(m-1) 成立來證明OM(m) m>0。

（1）首先考慮傳送命令的將軍是忠誠的。那麼將引理中k 設為m 則OM(m) 滿足IC2 ，IC1 在發令將軍是忠誠的情況下也滿足。 

（2）如果傳送命令的將軍是叛徒。那麼在下一輪中，總共有3m個副官，其中有m-1個副官是叛徒，有3m-(m-1)=2m+1個忠臣,

2m+1>m-1 即 在這裡所有的忠臣是可以達成一致的（這一步是為了說明OM（m-1）是成立的）。下面再推出OM（m-1）的表示式：這裡除去要傳送命令的一個將軍外還有超過3m-1個，有3m-1>3(m-1) 即 n'>3m'，所以在OM(m-1)是滿足條件的，得證。 

在這裡也同時證明了為什麼是m+1輪交換。因為OM（m）滿足。m->0 共 m+1;