最小堆操作(元素的新增和刪除)
先引用我一直很膜拜的牛人MoreWindows在堆排序中的一段內容,該內容詳細講述了最小堆,以及在最小堆中新增/刪除元素的原理。
二叉堆的定義
二叉堆是完全二叉樹或者是近似完全二叉樹。
二叉堆滿足二個特性:
1.父結點的鍵值總是大於或等於(小於或等於)任何一個子節點的鍵值。
2.每個結點的左子樹和右子樹都是一個二叉堆(都是最大堆或最小堆)。
當父結點的鍵值總是大於或等於任何一個子節點的鍵值時為最大堆。當父結點的鍵值總是小於或等於任何一個子節點的鍵值時為最小堆。下圖展示一個最小堆:
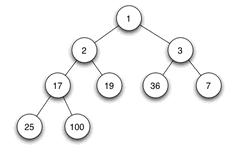
由於其它幾種堆(二項式堆,斐波納契堆等)用的較少,一般將二叉堆就簡稱為堆。
堆的操作——插入刪除
堆的儲存
一般都用陣列來表示堆,i結點的父結點下標就為(i – 1) / 2。它的左右子結點下標分別為2 * i + 1和2 * i + 2。如第0個結點左右子結點下標分別為1和2。

下面先給出《資料結構C++語言描述》中最小堆的建立插入刪除的圖解,再給出本人的實現程式碼,最好是先看明白圖後再去看程式碼。
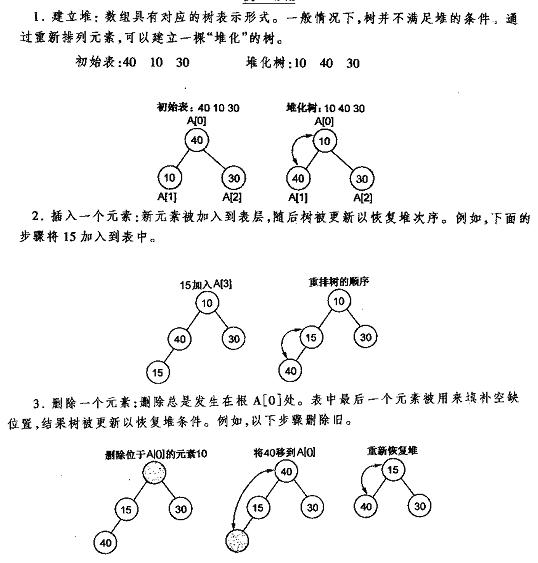
下面的內容是我自己編寫的一個在最小堆上新增、刪除元素的演算法示例。首先建立了一個堆操作的介面,方便以後對堆操作的擴充套件。
public interface HeapOperation { int[] addNumber(int[] array, int length, int num); int[] deleteNumber(int[] array, int length); }
1.最小堆新增元素
最小堆新增元素的操作流程類似於排序演算法之插入演算法,先將需要新增的元素插入陣列尾部,然後按照插入演算法對堆進行調整。public int[] addNumber(int[] array, int length, int num) { int[] newArray = new int[length + 1]; for(int i = 0; i < length; i++) { newArray[i] = array[i]; } newArray[length] = num; MinHeapFixup(newArray, length + 1); return newArray; }
private void MinHeapFixup(int[] array, int length) {
int i, j, temp;
temp = array[length - 1];
i = length - 1;
j = (i - 1) / 2;
while(j >= 0 && i != 0) {
if(array[j] < array[i]) {
break;
}
array[i] = array[j];
i = j;
j = (i - 1) / 2;
}
array[i] = temp;
}
對函式MinHeapFixup進行簡化,如下:
private void MinHeapFixup(int[] array, int i) {
int k = i - 1;
for(int j = (k-1)/2; j >= 0 && k!= 0 && array[j] > array[k]; k = j, j = (k-1)/2) {
swap(array, k, j);
}
}
其中swap函式是將陣列array的腳標為k和j的兩個元素進行交換。
private void swap(int[] array, int i, int j) {
array[i] = array[i] + array[j];
array[j] = array[i] - array[j];
array[i] = array[i] - array[j];
}
2.最小堆刪除元素
按照最小堆刪除元素步驟,演算法設計如下:public int[] deleteNumber(int[] array, int length) {
swap(array, 0, length - 1);
return MixHeapFixdown(array, 0, length - 1);
}
private int[] MixHeapFixdown(int[] array, int i, int n) {
int temp = array[i];
int j = 2 * i + 1;
int[] newArray = new int[n];
while(j < n) {
if(j + 1 < n && array[j] > array[j+1]) {
j++;
}
if(array[j] >= temp) {
break;
}
array[i] = array[j];
i = j;
j = 2 * i + 1;
}
array[i] = temp;
for(j = 0; j < n; j++) {
newArray[j] = array[j];
}
return newArray;
}
對上述演算法進行驗證,結果與理論結果一致。
public class Client {
private static void print(int[] array) {
for(int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
}
public static void main(String[] args) {
int[] array = {10, 40, 30};
MinHeapOperation mho = new MinHeapOperation();
int[] arrayForAdd = mho.addNumber(array, array.length, 15);
print(arrayForAdd);
System.out.println();
int[] arrayForDelete = mho.deleteNumber(arrayForAdd, arrayForAdd.length);
print(arrayForDelete);
}
}
相關推薦
最小堆操作(元素的新增和刪除)
先引用我一直很膜拜的牛人MoreWindows在堆排序中的一段內容,該內容詳細講述了最小堆,以及在最小堆中新增/刪除元素的原理。 二叉堆的定義 二叉堆是完全二叉樹或者是近似完全二叉樹。 二叉堆滿足二個特性: 1.父結點的鍵值總是大於或等於(小於或等於)任何一個子節
exchange webservice訪問類(日程新增和刪除)
輸出錯誤資訊: assistant.WriteFile("C:\\DEBUG.txt", "Length:" + diResponse.ResponseMessages.Items.Length.ToString()); assistant
輸出一個一維陣列中的最大值、最小值、全部元素的和,並將此陣列中的值按逆序重新存放。例如原先a[0]~a[4]存放2 8 7 5 3,逆序存放後 a[0]~a[4]變為存放3 5 7 8 2
#include <iostream> using namespace std; int main() {int a[5],d[5],i,k,m,n,p,sum,b,c; cout<<"please enter five numbers:"; for
【機器學習筆記02】最小二乘法(多元線性迴歸模型)
數學基礎 1.轉置矩陣 定義: 將矩陣A同序數的行換成列成為轉置矩陣ATA^TAT,舉例: A=(1203−11)A=\begin{pmatrix} 1 & 2 & 0 \\ 3 & -1 &
【機器學習筆記01】最小二乘法(一元線性迴歸模型)
【參考資料】 【1】《概率論與數理統計》 【2】 http://scikit-learn.org /stable/auto_examples/ linear_model/ plot_ols.html # sphx-glr-auto-examples-
009、最小的映象(2018-12-26 週三)
參考 https://www.cnblogs.com/CloudMan6/p/6788841.html 映象的內部結構 為後面製作映象做準備,先來分析一個簡單的映象 hello-world。
最小二乘法(自我理解+自我熟悉)(1)
最近一直在看機器學習的東西,看了好些論文,但奈何基礎實在太差,有很多東西都不懂。所以就看各種演算法。雖然當然看完覺得理解了,但一段時間過去又忘的差不多,無奈之舉,希望通過部落格來加深自己對基礎知識的理解和掌握。這次總結也是通過各種部落格和材料收集得到的,所以只能說是
字串最小表示法(LeetCode 899. Orderly Queue )
A string S of lowercase letters is given. Then, we may make any number of moves. In each move, we choose one of the first K letters (sta
把陣列中全部數拼接組合成一個最小的數(劍指offer筆記)
題目:輸入一個正整數陣列,把數組裡所有數字拼接起來排成一個數,列印能拼接出的所有數字中最小的一個。例如輸入陣列{3,32,321},則打印出這三個數字能排成的最小數字為321323。先附上程式碼,後面具體講解一下為何這樣寫以及程式碼中涉及到的python方法# -*- cod
牛客網《劍指Offer》程式設計 29. 最小的k個元素 (使用堆)
題目描述 輸入n個整數,找出其中最小的K個數。例如輸入4,5,1,6,2,7,3,8這8個數字,則最小的4個數字是1,2,3,4,。 解題思路 本題可以構建一個size為k的最大堆進行求解。 遍歷陣列。 當堆中元素總量小於k的時候,將當前元素放入堆; 當堆中元素總
1.給棧新增一個獲取最小值的方法(元素為Integer型),要求時間複雜度為O(1)
分析:在資料結構與演算法中,當要求時間複雜度最小時基本都是要犧牲空間複雜度。棧是先進後出,此處要求用棧實現一個獲取最小值的方法且時間複雜度為O(1),首先考慮的方向就是再借助一個棧來實現,這個棧主要用來儲存最小值序列(這個地方可以思考一下為什麼不能用一個變數來儲存最小值)。 下面直接附上程式碼:
演算法導論第三版第六章 合併K個有序連結串列的三種解法(最小堆法和分治遞迴法)
題目要求是將k個有序連結串列合併為一個連結串列,時間複雜度限定為O(nlogk)。下面給出應用最小堆方法的兩個程式,最後再貼上利用分治遞迴法的程式碼,雖然時間複雜度不及堆方法,但思路相對簡單好理解。 (1)最小堆方法1 用一個大小為K的最小堆(用優先佇列+自定義降序實現)(
(最小堆)哈夫曼樹 ->求結點值與權值積的和
#include<stdio.h> #include<string.h> #include<queue> #include<algorithm> using namespace std; priority_queue<
堆樹(最大堆和最小堆)
一、堆樹的定義堆樹的定義如下:(1)堆樹是一顆完全二叉樹;(2)堆樹中某個節點的值總是不大於或不小於其孩子節點的值;(3)堆樹中每個節點的子樹都是堆樹。當父節點的鍵值總是大於或等於任何一個子節點的鍵值時為最大堆。 當父節點的鍵值總是小於或等於任何一個子節點的鍵值時為最小堆。如
資料結構——最大堆和最小堆(C語言)
定義: 最大堆和最小堆都是一棵完全二叉樹。 最大堆:是指根節點的關鍵字值是堆中的最大關鍵字值,且每個節點若有兒子節點,其關鍵字值都不小於其兒子節點的關鍵字值。 最小堆:是指根節
用鄰接表和最小堆實現Dijkstra 最短路演算法 (Java實現)
演算法特點: 迪科斯徹演算法使用了廣度優先搜尋解決賦權有向圖或者無向圖的單源最短路徑問題,演算法最終得到一個最短路徑樹。該演算法常用於路由演算法或者作為其他圖演算法的一個子模組。 演算法的思路 Dijkstra演算法採用的是一種貪心的策略,宣告一個數
尋找一個數組中未出現的最小正整數(數組元素可重復)
個數 pre doesn inf tput swe return 分享圖片 針對 題目描述 Description Given nn non-negative integers, please find the least non-negative integer that
最大堆和最小堆
new clas 代碼 轉移 break OS 分支 -s std 參考:https://blog.csdn.net/guoweimelon/article/details/50904346 一、堆樹的定義 堆樹的定義如下: (1)堆樹是一顆完全二叉樹; (2)
python3-開發進階 heapq模塊(如何查找最大或最小的N個元素)
div lam 優勢 排序 portfolio res 函數 多個 items 一、怎樣從一個集合中獲得最大或者最小的 N 個元素列表? heapq 模塊有兩個函數:nlargest() 和 nsmallest() 可以完美解決這個問題。 import heap
最小函數值(堆)
輸入 之一 getch ont 我們 描述 a* algorithm int 最小函數值 題目描述 有n個函數,分別為F1,F2,...,Fn。定義Fi(x)=Aix^2+Bix+Ci (x∈N*)。給定這些Ai、Bi和Ci,請求出所有函數的所有函數值中最小的m個(如有重復
