http://blog.sina.com.cn/s/blog_4d7c97a00101cv5h.html

一、概念

英文名稱：white Gaussian noise; WGN
定義：均勻分佈於給定頻帶上的高斯噪聲；
所謂高斯白噪聲中的高斯是指概率分佈是正態函式，而白噪聲是指它的二階矩不相關，一階矩為常數，是指先後訊號在時間上的相關性。這是考察一個訊號的兩個不同方面的問題。
高斯白噪聲：如果一個噪聲，它的幅度服從高斯分佈，而它的功率譜密度又是均勻分佈的，則稱它為高斯白噪聲。
熱噪聲和散粒噪聲是高斯白噪聲。
二、matlab舉例
Matlab有兩個函式可以產生高斯白噪聲，wgn( )和awgn( )。

1. WGN：產生高斯白噪聲
y = wgn(m,n,p)
y = wgn(m,n,p) %產生一個m行n列的高斯白噪聲的矩陣，p以dBW為單位指定輸出噪聲的強度。
y = wgn(m,n,p,imp)
y = wgn(m,n,p,imp) %以歐姆(Ohm)為單位指定負載阻抗。
y = wgn(m,n,p,imp,state)
y = wgn(m,n,p,imp,state) %重置RANDN的狀態。

在數值變數後還可附加一些標誌性引數： 
y = wgn(…,POWERTYPE) 指定p的單位。POWERTYPE可以是'dBW', 'dBm'或'linear'。線性強度(linear power)以瓦特(Watt)為單位。 
y = wgn(…,OUTPUTTYPE) 指定輸出型別。OUTPUTTYPE可以是'real'或'complex'

2. AWGN：在某一訊號中加入高斯白噪聲
y = awgn(x,SNR)
y = awgn(x,SNR) %在訊號x中加入高斯白噪聲。信噪比SNR以dB為單位。x的強度假定為0dBW。如果x是 複數，就加入復噪聲。

y = awgn(x,SNR,SIGPOWER) 如果SIGPOWER是數值，則其代表以dBW為單位的訊號強度；如果SIGPOWER為'measured'，則函式將在加入噪聲之前測定訊號強度。 
y = awgn(x,SNR,SIGPOWER,STATE) 重置RANDN的狀態。 
y = awgn(…,POWERTYPE) 指定SNR和SIGPOWER的單位。POWERTYPE可以是'dB'或'linear'。如果POWERTYPE是'dB'，那麼SNR以dB為單位，而SIGPOWER以dBW為單位。如果POWERTYPE是'linear'，那麼SNR作為比值來度量，而SIGPOWER以瓦特為單位

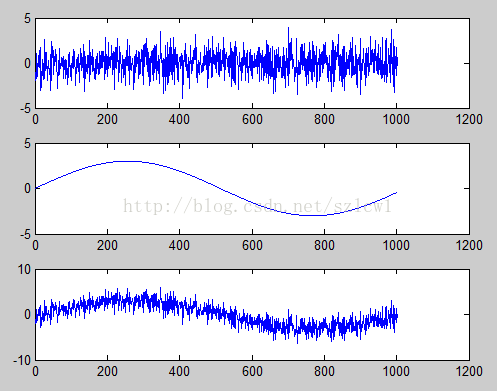
clear,clc;
N=0:1000;
fs=1024;
t=N./fs;
y=3*sin(2*pi*t);
x=wgn(1,1001,2);
i=y+x;
% i=awgn(y,2);
subplot(3,1,1),plot(x);
subplot(3,1,2),plot(y);
subplot(3,1,3),plot(i);

補充：

一階矩就是隨機變數的期望，二階矩就是隨機變數平方的期望，以此可以類推高階的矩。