opencv最小包絡矩形

阿新 • • 發佈：2019-01-20

RotatedRect cv::minAreaRect	(	InputArray 	points	)

小demo

cv::Mat inputMat(
            cvPoionts2d.size()/*std::vector<cv::Point2f>*/,
            2,
            cv::DataType<cv::Point2f::value_type>::type,
            cvPoionts2d.data()
        );

        cv::Point2f ans[4];
        cv::minAreaRect(inputMat)
            .points(ans);

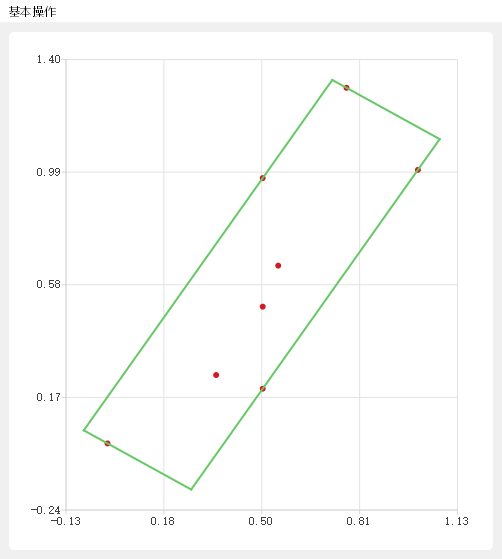
看了一下opencv的原始碼實現,基本步驟是先求凸包,然後用旋轉卡盤演算法求解的

這裡用到了2個知識,證明比較囉嗦,直接說結論

1.最小外包矩形的邊一定經過凸包的頂點

2.最小外包矩形至少有一個邊與凸包的邊重合

opencv最小包絡矩形

RotatedRect cv::minAreaRect ( InputArray points ) 小demo cv::Mat inputMat( cvPoionts2d.size()/*std::vector<cv::Point2f&

【Opencv】繪製最小外接矩形、最小外接圓

Opencv繪製最小外接矩形、最小外接圓 Opencv中求點集的最小外結矩使用方法minAreaRect，求點集的最小外接圓使用方法minEnclosingCircle。 minAreaRect方法原型： RotatedRect minAreaRect( Input

opencv中最小外接矩形2 的演算法

之前用到opencv最小外接矩形去表示一個類橢圓形的高度，特此記錄備查。對給定的 2D 點集，尋找最小面積的包圍矩形，使用函式： CvBox2DcvMinAreaRect2(constCvArr*points,CvMemStorage*storage=NULL);

Opencv獲取最小外接矩形——minAreaRect

//!computes the minimal rotated rectangle for a set of points RotatedRect minAreaRect(InputArray points);//計算一些列點的最小外接矩形，帶角度資訊 C+

OpenCV找出最小外接矩形

慣例先放結果吧測試圖片盜取自：地址（2333）其實就一行關鍵的程式碼： RotatedRect rect = minAreaRect(contours[i]);下面就是簡單粗暴的程

HDU 5988最小網絡流（浮點數）

blank empty pac scanf for continue -- math != 題目鏈接：http://acm.split.hdu.edu.cn/showproblem.php?pid=5988 哇，以前的模版一直T，加了優先隊列優化才擦邊過。建圖很好建，概率

BZOJ 1185: [HNOI2007]最小矩形覆蓋-旋轉卡殼法求點集最小外接矩形(面積)並輸出四個頂點坐標-備忘板子

article ref https color 旋轉 blank spa def abs 來源:旋轉卡殼法求點集最小外接矩形（面積）並輸出四個頂點坐標 BZOJ又崩了，直接貼一下人家的代碼。代碼: 1 #include"stdio.h"

OpenCV最小二乘法：cv::solve函式

OpenCV最小二乘法：cv::solve函式本例程通過opencv庫函式對一系列點進行三次曲線擬合，最小二乘法原理可自行百度理解 #include<iostream> #include<opencv2/opencv.hpp> usi

（五）建築物多邊形化簡系列——最小外接矩形的獲取

最小外接矩形問題是在給出一個多邊形（或一群點），求出面積最小且外接多邊形的矩形的問題。這個問題看起來並不難，但是具體實現並不簡單。除了呼叫現有的公開庫之外，這裡給出一種簡單且易理解的方法。演算法的主要思想是：（1）先實現多邊形的簡單外接矩形的演算法。簡單外接矩形是指邊平

C/C++ 影象處理（16）------影象輪廓の最小外接矩形

有時做影象處理，會遇到影象中大部分資訊是冗餘的情況，以下圖為例：假設圖中黑色部分才是我們需要研究的物件，則外圍的一堆白色是我們希望去掉的，這個時候用最小外接矩形來框住黑色部分，進而擷取該部分的資

opencv_tutorial_code學習——畫最小包圍旋轉矩形&畫最小包圍橢圓

tutorial_code\ShapeDescriptors\generalContours_demo2.cpp 步驟： 1、灰度化 2、濾波 3、二值化 4、畫輪廓 findContours（） 5、畫最小包圍旋轉矩形和最小包圍橢圓 vector<RotatedRe

最小外接矩形（ROI）

//---------------------------------【標頭檔案、名稱空間包含部分】---------------------------- // 描述：包含程式所使用的標頭檔案和名稱空間 //-------------------------------

OpenCV 最小二乘擬合方法求取直線傾角

工業相機拍攝的影象中，由於攝像質量的限制，影象中的直線經過處理後，會表現出比較嚴重的鋸齒。在這種情況下求取直線的傾角（其實就是直線的斜率），如果是直接選取直線的開始點和結束點來計算，或是用opencv自帶的哈夫曼直線方法，都會引起較大的角度偏差，一般會達到好幾度。誤差這

BZOJ 1185 [HNOI2007]最小矩形覆蓋：凸包 + 旋轉卡殼

read font return iostream operator 投影 class mod 平面題目鏈接：https://www.lydsy.com/JudgeOnline/problem.php?id=1185 題意：　　給出二維平面上的n個點，問你將所有點覆

[BZOJ1185][HNOI2007]最小矩形覆蓋-[凸包+旋轉卡殼]

col %d pac .com desc ret math n) abs Description 傳送門 Solution 感性理解一下，最小矩形一定是由一條邊和凸包上的邊重合的。然後它就是模板題了。。然而真的好難調，小於大於動不動就打錯。 Code #includ

0035-OpenCV環境下繪製輪廓的外接多邊形、最小立式矩形、最小外接圓

OpenCV提供了函式approxPolyDP()、boundRect()、minEnclosingCircle()分別計算給定點集的外接多邊形，最小立式矩形和最小外接圓，下面分別給出這三個函式的原型和引數意義。approxPolyDP函式(計算外接多邊形)： C++: void approxPol

OpenCV——邊界框、最小矩形區域和最小閉圓的輪廓

對下面這張影象，檢測其邊界框、最小矩形區域以及最小閉圓的輪廓。 hammer.jpg 使用cv2.pyrDown()函式縮小圖片。使用cv2.threshold()函式進行二值化處理。

【BZOJ1185】[HNOI2007]最小矩形覆蓋（凸包，旋轉卡殼）

tps 簡單的 double 所有 iostream ace str 覆蓋 cpp 【BZOJ1185】[HNOI2007]最小矩形覆蓋（凸包，旋轉卡殼）題面 BZOJ 洛谷題解最小的矩形一定存在一條邊在凸包上，那麽枚舉這條邊，我們還差三個點，即距離當前邊的最遠點，以

【洛谷 P3187】 [HNOI2007]最小矩形覆蓋（二維凸包，旋轉卡殼）

ref scanf const 維護 math int() 一個數據 pre 題目鏈接嗯，毒瘤題。首先有一個結論，就是最小矩形一定有條邊和凸包重合。腦補一下就好了。然後枚舉凸包的邊，用旋轉卡殼維護上頂點、左端點、右端點就好了。上頂點用叉積，叉積越大三角形面積越大，

BZOJ1185 HNOI2007 最小矩形覆蓋凸包、旋轉卡殼

amp cout 就是 max line fix bool 一個輸出傳送門首先，肯定只有凸包上的點會限制這個矩形，所以建立凸包。然後可以知道，矩形上一定有一條邊與凸包上的邊重合，否則可以轉一下使得它重合，答案會更小。於是沿著凸包枚舉這一條邊，通過旋轉卡殼找到離這

opencv最小包絡矩形

相關推薦