最近用到影象中的點的聚類，於是就寫了一個k-means的類。

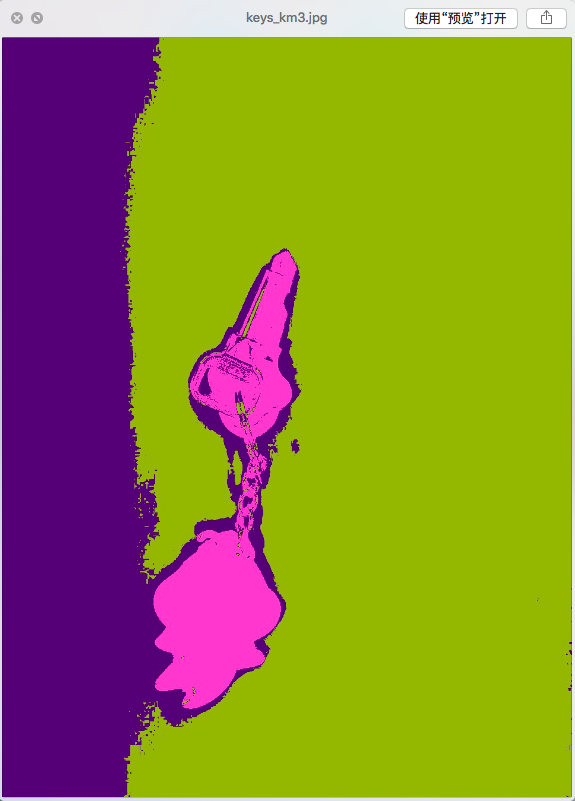
驗證的過程是將一幅圖的所有點的(B, G, R)作為資料點，進行聚類。

算出K箇中心類後，對影象中的每個點進行重新上色。按照類別給給每類生成一種隨機色彩。

使用該類，可以自定義聚類中心K的個數、資料維度N的大小。

資料型別可以是float、int。

同時在迭代過程中，可以選擇輸出每次迭代的中心點資訊等。

下面分以下幾個部分：

一，K-means的思路

二，基本公式與程式實現細節

三，參考

四，影象處理結果

----------------------------------------------------------------------------------------------------------------------------

K-means 演算法是一種簡單有效的無監督學習方法，它可以有效地將多維空間（用N表示）中的點聚成一個個緊密的簇。

K-means演算法的優化目標是使求出K箇中心點，使每一個點到該點的歐氏距離平方之和儘量小（不知道現在有沒有什麼演算法能保證一定得到全域性最優解）。

簡單來說就是把一個分到一個類中的所有資料點的每一維相加，得一個向量。然後，該向量的每一維除以該類的點的個數。這樣得的向量就是該類的中心(centroid).

演算法的思路如下：

1. 初始化K箇中心點。

這K個點可以是在所有輸入資料點中隨機抽取的，也可以是取前K個點，也可以是從N維空間中任意一個點。這些點和資料點之間的距離只要不是相差的太離譜都沒有關係。

2. 對任意一個數據點，求與它最近的中心點，並認為該資料點屬於該中心點所代表的類。對於M(假設共有M個數據點）個數據點，分別計算每個點與K個當前的中心點的歐氏距離平方值，點x_i與哪個中心點（如c_j）的歐氏距離平方最小那麼它就分成該類。（該過程可以求出一些指標，用於終止程式。如，求出整體歐氏距離之和）

一般暴力的方法是要計算M * K次歐氏距離。《An Efficient k-Means Clustering Algorithm:Analysis and Implementation》 提供了一種利用KD樹的超子空間到K個點心點的距離對中心點進行減枝的方法。它的主要思想是，將一個KD樹中的子空間作為一個超球面的中心點，以K箇中心點中到子空間中心最近的距離為半徑形成了一個新的超球面，用這個超球面將當前的K箇中心點分成兩部分：與該子空間的最近中心點的待選集合與不可能是該子空間中任意一點的最近中心點的集合。

3. 更新每個類的中心點。

4. 由 2 得出的指標判斷是否可以終止：否，進行 2 ；是，終止，並給出中心點資訊。

----------------------------------------------------------------------------------------------------------------------------

程式實現細節：

0. K-means類定義。這個程式的一部分目的也是為了測試類模版，原本想相容多種資料型別（float、int），到最後才發現主要還是對float型別做處理。(所以使用類模版在這個程式中有點雞肋。完全可以用float代替。維度N也是同樣的，維度N和待求中心點的個數K都可以在類宣告時候定義）

template <typename T, int N> class KMeansTest
{
private:
    vector<vector<T>> centers;// 儲存中心點
    bool data_is_ok(vector<vector<T>> points, int k);
    T calculate_center_once(vector<vector<T>> points);// calculate centers for once, and return the total sum
    int k_centers = 0;
    T Total_Sum = 0; // sum of square, or square root of sum
    T Total_Sum_Sqrt = 0; // sum of square, or square root of sum
public:
    int end_modal = 0;
    bool random_initial_centers = false; // trye: get random points as centers; else, get top k points as initial centers.
    bool show_info_flag = false; // true: show kmeans object centers' information; false: show output only.
    KMeansTest();
    KMeansTest(vector<vector<T>> points, int k);
    void init_k(vector<vector<T>> points, int k);
    int get_centers(vector<T> point); // return the center index and center point
    void show_info();
    void sort_ascend(); // sort average of each point in ascend order.
};

1. 初始化。我設定了兩種可以初始化的方式：取前K個點；隨機取K個點。程式碼如下：

    if (random_initial_centers) {
        
        for (int i = 0; i < k; i++) {
            int iSecret;
            
            srand (time(0)+i);// use current time as seed for random generator
            
            iSecret = rand() % points.size();
            centers.push_back(points[iSecret]);
        }
    }
    else
    {
        for (int i = 0; i < k; i++) {
            centers.push_back(points[i]);
        }
    }

    T total_sum = 0; //
    
    // initialize clusters storage
    //    vector<vector<vector<T>>> clusters(N, vector<vector<T>>);
    
    map<int, vector<vector<T>>> clusters;
    // calculate square sum
    for (typename vector<vector<T>>::iterator it = points.begin(); it!=points.end(); it++) {
        
        ////////////// BEGIN: find the nearest center, and the minimum squared distance///////////////
        T min = ((*it)[0]-centers[0][0]) * ((*it)[0]-centers[0][0]); // how to find the maximum of Type T, and initialize 0 to T?
        //
        for (int i=1; i<N; i++) {
            min += ((*it)[i]-centers[0][i]) * ((*it)[i]-centers[0][i]);
        }
        
        //        cout<<"Begin min:"<<min<<endl;
        int min_i = 0;// the nearest center's index
        
        for (int i = 1; i<k_centers; i++) { // k, centers
            // test
            
            T sum = ((*it)[0]-centers[i][0]) * ((*it)[0]-centers[i][0]);
            //            cout<<"sum: "<<sum<<"\t";
            for (int j = 1; j<N; j++) { // N, dimension
                // WRONG FORMAT:                sum += (*it[j]-centers[i][j]) * (*it[j]-centers[i][j]);
                sum += ((*it)[j]-centers[i][j]) * ((*it)[j]-centers[i][j]);
                //                cout<<sum<<"\t";
            }
            //            cout<<"compare sum and min||sum:"<<sum<<"||min:"<<min<<"||sum<min:"<<(sum<min)<<endl;
            if (sum < min) {
                //                waitKey(0);
                min = sum;
                min_i = i;
                //                cout<<"EXCANG: min:"<<min<<"\t min_i:"<<min_i<<"\t";
            }
            //            cout<<endl;
        }
        /////////////// END: find the nearest center, and the minimum squared distance///////////////
        
        /////////////// store points for cluster min_i /////////////////////////
        clusters[min_i].push_back(*it); // save point to cluster min_i
        total_sum += min;
        //        cout<<"min: "<<min<<"\ttotal_sum:"<<total_sum<<endl;
    }
 

3. 更新中心點。

    //////////////////// update centers /////////////////////
    
    for (int i = 0; i < k_centers; i++) {
        
        if (clusters.find(i)==clusters.end()) // if there is no point assigned to this center, do nothing about it. You can also change this center by random, or some also policy.®
        {
            continue;
        }
        vector<T> center = clusters[i][0];
        
        
        
        int c_i_size = (int)clusters[i].size(); // might be wrong , when initial centers are same
        
        // if there is no point in cluster[i], continue
        //        if (c_i_size==0) {
        //            continue;
        //        }
        
        for (int j=1; j<c_i_size; j++) {
            for (int d = 0; d < N; d++) {
                center[d] += clusters[i][j][d]; // might be wrong , when initial centers are same.
            }
        }
        
        // update centers
        centers[i].clear();
        for (int d = 0; d < N; d++) {
            centers[i].push_back(center[d]/c_i_size);
        }
    }
    
    Total_Sum_Sqrt = sqrt(total_sum);
    //    Total_Sum = total_sum;

4. 終止步驟 2 和 3 的迭代過程的條件可以自己選擇，比如：

a. 設定迭代次數

b. 分配給每個類的點數不再變動

c. 中心點不再變動

d. 整體歐氏距離平方和不再變動

e. 整體歐氏距離平方和小於某個閾值

在這裡我用了條件 d，同時我也在尋找過程中記錄了整體歐氏距離平方和最小情況下的中心點資訊。

實踐經驗是：K-means收斂挺快，還沒遇到過無限迭代的情況；整體歐氏距離平方和有時候會先下降到一定程度，然後再稍稍上升一點，目前還不知道為什麼；下面這兩種方式先出來的中心點一般差別不大，在實驗的圖片上的效果看不出差別。

程式碼如下：

   switch (end_modal) {
        case 0:
        {
            do{
                pre_sum = total_sum;
                //        show_info();
                total_sum = calculate_center_once(points);
            }while (pre_sum-total_sum);
            
        }
            break;
        case 1:
        {
            T min_sum = total_sum;
            tem_centers = centers;
            do{
                pre_sum = total_sum;
                show_info();
                total_sum = calculate_center_once(points);
                
                if (min_sum > total_sum) {
                    min_sum = total_sum;
                    //                     tem_centers.clear();
                    tem_centers = centers;
                }
            }while (pre_sum-total_sum);
            
            //            centers.clear();
            centers = tem_centers;
            Total_Sum_Sqrt = min_sum;
            
        }
            break;
        default:
            break;
    }

----------------------------------------------------------------------------------------------------------------------------

同時，我對一張圖片進行了一些測試。

原圖：

聚3類：

聚4類：

聚7類：

聚10類：

聚20類：