宣告：程式碼的執行環境為Python3。Python3與Python2在一些細節上會有所不同，希望廣大讀者注意。本部落格以程式碼為主，程式碼中會有詳細的註釋。相關文章將會發布在我的個人部落格專欄《Python從入門到深度學習》，歡迎大家關注~

       根據訓練樣本是否包含標籤資訊，機器學習可以分為監督學習和無監督學習（這裡我們不考慮半監督學習）。聚類演算法是典型的無監督學習演算法，它是對事務自動歸類的一種演算法，在聚類演算法中利用樣本的標籤，將具有相似屬性的事物聚集到一類中。

一、常用的相似性度量

        K-Means演算法（K-均值演算法）是基於相似性的無監督學習演算法，即通過比較樣本之間的相似性，將較為相似的樣本劃分到同一個類別中。為了度量兩個樣本（以樣本X和樣本Y為例）之間的相似性，通常會定義一個距離函式d(X,Y)，利用這個距離函式來定義樣本X和樣本Y之間的相似性。

1、閔可夫斯基距離

        空間中兩個點X，Y的座標分別為：

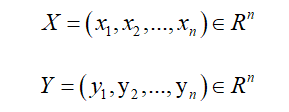
        那麼，點X與點Y之間的閔可夫斯基距離可以定義為：

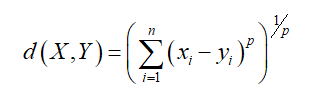
2、曼哈頓距離

        同樣的兩個點X，Y其曼哈頓距離可以表示為：

3、歐氏距離

        同樣的，點X與點Y的歐氏距離可以表示為：

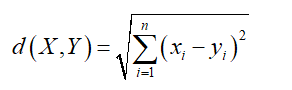
        由上面的定義可知，曼哈頓距離和歐式距離是閔可夫斯基距離的特殊形式。當p=1時，閔可夫斯基距離就是曼哈頓距離；當p=2時，閔可夫斯基距離就是歐式距離。在K-Means演算法中，我們使用歐氏距離作為其相似性度量。因為歐氏距離的根號存在與否對其度量性沒有影響，簡單起見，我們使用歐氏距離的平方作為最終的相似性度量。

        首先將需要載入相關的模組：

import numpy as np

       歐氏距離的平方實現程式碼如下：

def distance(vecA, vecB):
    '''
    計算兩個向量之間歐氏距離的平方
    :param vecA: 向量A的座標
    :param vecB: 向量B的座標
    :return: 返回兩個向量之間歐氏距離的平方
    '''
    dist = (vecA - vecB) * (vecA - vecB).T
    return dist[0, 0]

二、K-Means演算法原理

        首先，我們需要人為的指定最終的聚類個數，假設我們最終的聚類個數為k個，即我們需要初始化k個聚類中心，通過計算每個樣本與聚類中心的相似度，將樣本點劃分到距離最近的聚類中心。然後，通過每個類的樣本重新計算每個類的聚類中心，重複這個操作直至聚類中心不再改變即為最終的聚類結果。

三、K-Means演算法步驟

        1、隨機初始化K個聚類中心，其程式碼如下：

def randomCenter(data, k):
    '''
    隨機初始化聚類中心
    :param data: 訓練資料
    :param k: 聚類中心的個數
    :return: 返回初始化的聚類中心
    '''
    n = np.shape(data)[1]  # 特徵的個數
    cent = np.mat(np.zeros((k, n)))  # 初始化K個聚類中心
    for j in range(n):  # 初始化聚類中心每一維的座標
        minJ = np.min(data[:, j])
        rangeJ = np.max(data[:, j]) - minJ
        cent[:, j] = minJ * np.mat(np.ones((k, 1))) + np.random.rand(k, 1) * rangeJ  # 在最大值和最小值之間初始化
    return cent

         2、計算每個樣本與k個聚類中心的相似度，將樣本劃分到與之最相似的類中；

         3、計算劃分到每個類別中所有樣本特徵的均值，並將該均值作為每個類別新的聚類中心；

         4、重複2、3步操作，直至聚類中心不再改變，輸出最終的聚類中心。

         構建K-Means演算法的程式碼如下：

def kmeans(data, k, cent):
    '''
    kmeans演算法求解聚類中心
    :param data: 訓練資料
    :param k: 聚類中心的個數
    :param cent: 隨機初始化的聚類中心
    :return: 返回訓練完成的聚類中心和每個樣本所屬的類別
    '''
    m, n = np.shape(data)  # m：樣本的個數；n：特徵的維度
    subCenter = np.mat(np.zeros((m, 2)))  # 初始化每個樣本所屬的類別
    change = True  # 判斷是否需要重新計算聚類中心
    while change == True:
        change = False  # 重置
        for i in range(m):
            minDist = np.inf  # 設定樣本與聚類中心的最小距離，初始值為正無窮
            minIndex = 0  # 所屬的類別
            for j in range(k):
                # 計算i和每個聚類中心的距離
                dist = distance(data[i, ], cent[j, ])
                if dist < minDist:
                    minDist = dist
                    minIndex = j
            # 判斷是否需要改變
            if subCenter[i, 0] != minIndex:  # 需要改變
                change = True
                subCenter[i, ] = np.mat([minIndex, minDist])
        # 重新計算聚類中心
        for j in range(k):
            sum_all = np.mat(np.zeros((1, n)))
            r = 0  # 每個類別中樣本的個數
            for i in range(m):
                if subCenter[i, 0] == j:  # 計算第j個類別
                    sum_all += data[i, ]
                    r += 1
            for z in range(n):
                try:
                    cent[j, z] = sum_all[0, z] / r
                except:
                    print("ZeroDivisionError: division by zero")
    return subCenter, cent

四、K-Means演算法舉例

1、資料集：資料集含有兩個特徵，如下圖所示：

2、載入資料集

       我們此處使用如下方法載入資料集，也可使用其他的方式進行載入，此處可以參考我的另外一篇文章《Python兩種方式載入檔案內容》。載入檔案內容程式碼如下：

def load_data(file_path):
    '''
    匯入資料
    :param file_path: 檔案路徑
    :return: 以矩陣的形式返回匯入的資料
    '''
    f = open(file_path)
    data = []
    for words in f.readlines():
        row = []  # 記錄每一行
        word = words.strip().split("\t")
        for x in word:
            row.append(float(x))  # 將文字中的特徵轉換成浮點數
        data.append(row)
    f.close()
    return np.mat(data)  # 以矩陣的形式返回

3、儲存聚類結果

       通過K-Means聚類之後，我們可以使用如下方法儲存聚類結果：

def save_result(file_name, data):
    '''
    儲存source中的結果到file_name檔案中
    :param file_name: 儲存的檔名
    :param data: 需要儲存的資料
    :return:
    '''
    m, n = np.shape(data)
    f = open(file_name, "w")
    for i in range(m):
        tmp = []
        for j in range(n):
            tmp.append(str(data[i, j]))
        f.write("\t".join(tmp) + "\n")
    f.close()

4、呼叫K-Means演算法

       呼叫K-Means演算法：

if __name__ == "__main__":
    k = 4  # 聚類中心的個數
    file_path = "tfidf.txt"
    subCenter, center = kmeans(data, k, randomCenter(load_data(file_path), k))
    save_result("result/kmeans_sub", subCenter)
    save_result("result/kmeans_center", center)

5、結果展示

       得到的聚類結果如圖所示：

        你們在此過程中遇到了什麼問題，歡迎留言，讓我看看你們都遇到了哪些問題。