【特徵匹配】SIFT原理與C原始碼剖析
SIFT的原理已經有很多大牛的部落格上做了解析,本文重點將以Rob Hess等人用C實現的程式碼做解析,結合程式碼SIFT原理會更容易理解。一些難理解點的用了☆標註。
歡迎大家批評指正!
轉載請註明出處:http://blog.csdn.net/luoshixian099/article/details/47377611
SIFT(Scale-invariant feature transform)即尺度不變特徵轉換,提取的區域性特徵點具有尺度不變性,且對於旋轉,亮度,噪聲等有很高的穩定性。
下圖中,涉及到影象的旋轉,仿射,光照等變化,SIFT演算法依然有很好的匹配效果。
SIFT特徵點提取
本文將以下函式為參照順序介紹SIFT特徵點提取與描述方法。1.影象預處理
2.構建高斯金字塔(不同尺度下的影象)
3.生成DOG尺度空間
4.關鍵點搜尋與定位
5.計算特徵點所在的尺度
6.為特徵點分配方向角
7.構建特徵描述子
/** Finds SIFT features in an image using user-specified parameter values. All detected features are stored in the array pointed to by \a feat. */ int _sift_features( IplImage* img, struct feature** feat, int intvls, double sigma, double contr_thr, int curv_thr, int img_dbl, int descr_width, int descr_hist_bins ) { IplImage* init_img; IplImage*** gauss_pyr, *** dog_pyr; CvMemStorage* storage; CvSeq* features; int octvs, i, n = 0; /* check arguments */ if( ! img ) fatal_error( "NULL pointer error, %s, line %d", __FILE__, __LINE__ ); if( ! feat ) fatal_error( "NULL pointer error, %s, line %d", __FILE__, __LINE__ ); /* build scale space pyramid; smallest dimension of top level is ~4 pixels */ init_img = create_init_img( img, img_dbl, sigma ); //對進行圖片預處理 octvs = log( MIN( init_img->width, init_img->height ) ) / log(2) - 2; //計算高斯金字塔的組數(octave),同時保證頂層至少有4個畫素點 gauss_pyr = build_gauss_pyr( init_img, octvs, intvls, sigma ); //建立高斯金字塔 dog_pyr = build_dog_pyr( gauss_pyr, octvs, intvls ); //DOG尺度空間 storage = cvCreateMemStorage( 0 ); features = scale_space_extrema( dog_pyr, octvs, intvls, contr_thr, //極值點檢測,並去除不穩定特徵點 curv_thr, storage ); calc_feature_scales( features, sigma, intvls ); //計算特徵點所在的尺度 if( img_dbl ) adjust_for_img_dbl( features ); //如果影象初始被擴大了2倍,所有座標與尺度要除以2 calc_feature_oris( features, gauss_pyr ); //計算特徵點所在尺度內的方向角 compute_descriptors( features, gauss_pyr, descr_width, descr_hist_bins );//計算特徵描述子 128維向量 /* sort features by decreasing scale and move from CvSeq to array */ cvSeqSort( features, (CvCmpFunc)feature_cmp, NULL ); //對特徵點按尺度排序 n = features->total; *feat = calloc( n, sizeof(struct feature) ); *feat = cvCvtSeqToArray( features, *feat, CV_WHOLE_SEQ ); for( i = 0; i < n; i++ ) { free( (*feat)[i].feature_data ); (*feat)[i].feature_data = NULL; } cvReleaseMemStorage( &storage ); cvReleaseImage( &init_img ); release_pyr( &gauss_pyr, octvs, intvls + 3 ); release_pyr( &dog_pyr, octvs, intvls + 2 ); return n; }
—————————————————————————————————————————————————————
1.影象預處理
lowe建議把初始影象放大二倍,可以得到更多的特徵點,提取到更多細節,並且認為影象在尺度σ = 0.5時影象最清晰,初始高斯尺度為σ = 1.6。 ☆第19行因為影象被放大二倍,此時σ = 1.0 。因為對二倍化後的影象平滑是在σ = 0.5 上疊加的高斯模糊, 所以有模糊係數有sig_diff = sqrt (sigma *sigma - 0.5*0.5*4)=sqrt(1.6*1.6 -1) ;/************************ Functions prototyped here **************************/ /* Converts an image to 8-bit grayscale and Gaussian-smooths it. The image is optionally doubled in size prior to smoothing. @param img input image @param img_dbl if true, image is doubled in size prior to smoothing @param sigma total std of Gaussian smoothing */ static IplImage* create_init_img( IplImage* img, int img_dbl, double sigma ) { IplImage* gray, * dbl; double sig_diff; gray = convert_to_gray32( img ); //轉換為32位灰度圖 if( img_dbl ) // 影象被放大二倍 { sig_diff = sqrt( sigma * sigma - SIFT_INIT_SIGMA * SIFT_INIT_SIGMA * 4 ); // sigma = 1.6 , SIFT_INIT_SIGMA = 0.5 lowe認為影象在尺度0.5下最清晰 dbl = cvCreateImage( cvSize( img->width*2, img->height*2 ), IPL_DEPTH_32F, 1 ); cvResize( gray, dbl, CV_INTER_CUBIC ); //雙三次插值方法 放大影象 cvSmooth( dbl, dbl, CV_GAUSSIAN, 0, 0, sig_diff, sig_diff ); //高斯平滑 cvReleaseImage( &gray ); return dbl; } else { sig_diff = sqrt( sigma * sigma - SIFT_INIT_SIGMA * SIFT_INIT_SIGMA ); cvSmooth( gray, gray, CV_GAUSSIAN, 0, 0, sig_diff, sig_diff ); // 高斯平滑 return gray; } }
2.構建高斯金字塔
構建高斯金字塔過程即構建出影象在不同尺度上影象,提取到的特徵點可有具有尺度不變性。 影象的尺度空間L(x,y,σ)可以用一個高斯函式G(x,y,σ)與影象I(x,y)卷積產生,即L(x,y,σ) = G(x,y,σ) * I(x,y) 其中二維高斯核的計算為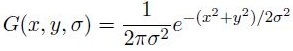 。
☆不同的尺度空間即用不同的高斯核函式平滑影象, 平滑係數越大,影象越模糊。即模擬出動物的視覺效果,因為事先不知道物體的大小,在不同的尺度下,影象的細節會表現的不同。當尺度由小變大的過程中,是一個細節逐步簡化的過程,影象中特徵不夠明顯的物體,就模糊的多了,而有些物體還可以看得到大致的輪廓。所以要在不同尺度下,觀察物體的尺度響應,提取到的特徵才能具有尺度不變性。
SIFT演算法採用高斯金字塔實現連續的尺度空間的影象。金字塔共分為O(octave)組,每組有S(intervals)層 ,下一組是由上一組隔點取樣得到(即降2倍解析度),這是為了減輕卷積運算的工作量。
構建高斯金字塔(octave = 5, intervals +3=6):
。
☆不同的尺度空間即用不同的高斯核函式平滑影象, 平滑係數越大,影象越模糊。即模擬出動物的視覺效果,因為事先不知道物體的大小,在不同的尺度下,影象的細節會表現的不同。當尺度由小變大的過程中,是一個細節逐步簡化的過程,影象中特徵不夠明顯的物體,就模糊的多了,而有些物體還可以看得到大致的輪廓。所以要在不同尺度下,觀察物體的尺度響應,提取到的特徵才能具有尺度不變性。
SIFT演算法採用高斯金字塔實現連續的尺度空間的影象。金字塔共分為O(octave)組,每組有S(intervals)層 ,下一組是由上一組隔點取樣得到(即降2倍解析度),這是為了減輕卷積運算的工作量。
構建高斯金字塔(octave = 5, intervals +3=6):
 全部空間尺度為:
全部空間尺度為:
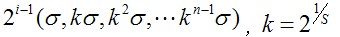 ☆1.這個尺度因子都是在原圖上進行的,而在演算法實現過程中,採用高斯平滑是在上一層影象上再疊加高斯平滑,即我們在程式中看到的平滑因子為
☆1.這個尺度因子都是在原圖上進行的,而在演算法實現過程中,採用高斯平滑是在上一層影象上再疊加高斯平滑,即我們在程式中看到的平滑因子為
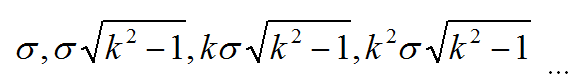 Eg. 在第一層上為了得到kσ的高斯模糊影象,可以在原圖上直接採用kσ平滑,也可以在上一層影象上(已被σ平滑)的影象上採用平滑因子為
Eg. 在第一層上為了得到kσ的高斯模糊影象,可以在原圖上直接採用kσ平滑,也可以在上一層影象上(已被σ平滑)的影象上採用平滑因子為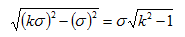 平滑影象,效果是一樣的。
☆2.我們在原始碼上同時也沒有看到組間的2倍的關係,實際在對每組的平滑因子都是一樣的,2倍的關係是由於在降取樣的過程中產生的,第二層的第一張圖是由第一層的平滑因子為2σ的影象上(即倒數第三張)降取樣得到,此時影象平滑因子為σ,所以繼續採用以上的平滑因子。但在原圖上看,形成了全部的空間尺度。
☆3.每組(octave)有S+3層影象,是由於在DOG尺度空間上尋找極值點的方法是在一個立方體內進行,即上下層比較,所以不在DOG空間的第一層與最後一層尋找,即DOG需要S+2層影象,由於DOG尺度空間是由高斯金字塔相鄰影象相減得到,即每組需要S+3層影象。
平滑影象,效果是一樣的。
☆2.我們在原始碼上同時也沒有看到組間的2倍的關係,實際在對每組的平滑因子都是一樣的,2倍的關係是由於在降取樣的過程中產生的,第二層的第一張圖是由第一層的平滑因子為2σ的影象上(即倒數第三張)降取樣得到,此時影象平滑因子為σ,所以繼續採用以上的平滑因子。但在原圖上看,形成了全部的空間尺度。
☆3.每組(octave)有S+3層影象,是由於在DOG尺度空間上尋找極值點的方法是在一個立方體內進行,即上下層比較,所以不在DOG空間的第一層與最後一層尋找,即DOG需要S+2層影象,由於DOG尺度空間是由高斯金字塔相鄰影象相減得到,即每組需要S+3層影象。/*
Builds Gaussian scale space pyramid from an image
@param base base image of the pyramid
@param octvs number of octaves of scale space
@param intvls number of intervals per octave
@param sigma amount of Gaussian smoothing per octave
@return Returns a Gaussian scale space pyramid as an octvs x (intvls + 3)
array
給定組數(octave)和層數(intvls),以及初始平滑係數sigma,構建高斯金字塔
返回的每組中層數為intvls+3
*/
static IplImage*** build_gauss_pyr( IplImage* base, int octvs,
int intvls, double sigma )
{
IplImage*** gauss_pyr;
const int _intvls = intvls; // lowe 採用了每組層數(intvls)為 3
// double sig_total, sig_prev;
double k;
int i, o;
double *sig = (double *)malloc(sizeof(int)*(_intvls+3)); //儲存每組的高斯平滑因子,每組對應的平滑因子都相同
gauss_pyr = calloc( octvs, sizeof( IplImage** ) );
for( i = 0; i < octvs; i++ )
gauss_pyr[i] = calloc( intvls + 3, sizeof( IplImage *) );
/*
precompute Gaussian sigmas using the following formula:
\sigma_{total}^2 = \sigma_{i}^2 + \sigma_{i-1}^2
sig[i] is the incremental sigma value needed to compute
the actual sigma of level i. Keeping track of incremental
sigmas vs. total sigmas keeps the gaussian kernel small.
*/
k = pow( 2.0, 1.0 / intvls ); // k = 2^(1/S)
sig[0] = sigma;
sig[1] = sigma * sqrt( k*k- 1 );
for (i = 2; i < intvls + 3; i++)
sig[i] = sig[i-1] * k; //每組對應的平滑因子為 σ , sqrt(k^2 -1)* σ, sqrt(k^2 -1)* kσ , ...
for( o = 0; o < octvs; o++ )
for( i = 0; i < intvls + 3; i++ )
{
if( o == 0 && i == 0 )
gauss_pyr[o][i] = cvCloneImage(base); //第一組,第一層為原圖
/* base of new octvave is halved image from end of previous octave */
else if( i == 0 )
gauss_pyr[o][i] = downsample( gauss_pyr[o-1][intvls] ); //第一層影象由上一層倒數第三張隔點取樣得到
/* blur the current octave's last image to create the next one */
else
{
gauss_pyr[o][i] = cvCreateImage( cvGetSize(gauss_pyr[o][i-1]),
IPL_DEPTH_32F, 1 );
cvSmooth( gauss_pyr[o][i-1], gauss_pyr[o][i],
CV_GAUSSIAN, 0, 0, sig[i], sig[i] ); //高斯平滑
}
}
return gauss_pyr;
}3.生成DOG尺度空間
Lindeberg發現高斯差分函式(Difference of Gaussian ,簡稱DOG運算元)與尺度歸一化的高斯拉普拉斯函式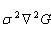 非常近似,且
非常近似,且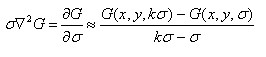
差分近似:
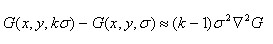
lowe建議採用相鄰尺度的影象相減來獲得高斯差分影象D(x,y,σ)來近似LOG來進行極值檢測。 D(x,y,σ) = G(x,y,kσ)*I(x,y)-G(x,y,σ)*I(x,y) =L(x,y,kσ) - L(x,y,σ) 對高斯金字塔的每組內相鄰影象相減,形成DOG尺度空間,這時DOG中每組有S+2層影象
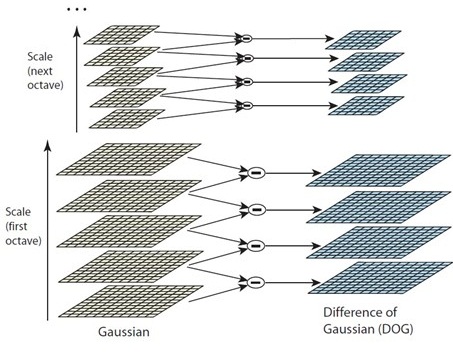
static IplImage*** build_dog_pyr( IplImage*** gauss_pyr, int octvs, int intvls )
{
IplImage*** dog_pyr;
int i, o;
dog_pyr = calloc( octvs, sizeof( IplImage** ) );
for( i = 0; i < octvs; i++ )
dog_pyr[i] = calloc( intvls + 2, sizeof(IplImage*) );
for( o = 0; o < octvs; o++ )
for( i = 0; i < intvls + 2; i++ )
{
dog_pyr[o][i] = cvCreateImage( cvGetSize(gauss_pyr[o][i]),
IPL_DEPTH_32F, 1 );
cvSub( gauss_pyr[o][i+1], gauss_pyr[o][i], dog_pyr[o][i], NULL ); //相鄰兩層影象相減,結果放在dog_pyr陣列內
}
return dog_pyr;
}4.關鍵點搜尋與定位
在DOG尺度空間上,首先尋找極值點,插值處理,找到準確的極值點座標,再排除不穩定的特徵點(邊界點)/*
Detects features at extrema in DoG scale space. Bad features are discarded
based on contrast and ratio of principal curvatures.
@return Returns an array of detected features whose scales, orientations,
and descriptors are yet to be determined.
*/
static CvSeq* scale_space_extrema( IplImage*** dog_pyr, int octvs, int intvls,
double contr_thr, int curv_thr,
CvMemStorage* storage )
{
CvSeq* features;
double prelim_contr_thr = 0.5 * contr_thr / intvls; //極值比較前的閾值處理
struct feature* feat;
struct detection_data* ddata;
int o, i, r, c;
features = cvCreateSeq( 0, sizeof(CvSeq), sizeof(struct feature), storage );
for( o = 0; o < octvs; o++ ) //對DOG尺度空間上,遍歷從第二層影象開始到倒數第二層影象上,每個畫素點
for( i = 1; i <= intvls; i++ )
for(r = SIFT_IMG_BORDER; r < dog_pyr[o][0]->height-SIFT_IMG_BORDER; r++)
for(c = SIFT_IMG_BORDER; c < dog_pyr[o][0]->width-SIFT_IMG_BORDER; c++)
/* perform preliminary check on contrast */
if( ABS( pixval32f( dog_pyr[o][i], r, c ) ) > prelim_contr_thr ) // 排除畫素值小於閾值prelim_contr_thr的點,提高穩定性
if( is_extremum( dog_pyr, o, i, r, c ) ) //與周圍26個畫素值比較,是否極大值或者極小值點
{
feat = interp_extremum(dog_pyr, o, i, r, c, intvls, contr_thr); //插值處理,找到準確的特徵點座標
if( feat )
{
ddata = feat_detection_data( feat );
if( ! is_too_edge_like( dog_pyr[ddata->octv][ddata->intvl], //根據Hessian矩陣 判斷是否為邊緣上的點
ddata->r, ddata->c, curv_thr ) )
{
cvSeqPush( features, feat ); //是特徵點進入特徵點序列
}
else
free( ddata );
free( feat );
}
}
return features;
}4.1
尋找極值點
在DOG尺度空間上,每組有S+2層影象,每一組都從第二層開始每一個畫素點都要與它相鄰的畫素點比較,看是否比它在影象域或尺度域的所有點的值大或者小。與它同尺度的相鄰畫素點有8個,上下相鄰尺度的點共有2×9=18,共有26個畫素點。也就在一個3×3的立方體內進行。搜尋的過程是第二層開始到倒數第二層結束,共檢測了octave組,每組S層。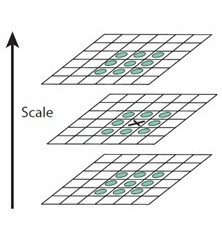
/*
Determines whether a pixel is a scale-space extremum by comparing it to it's
3x3x3 pixel neighborhood.
*/
static int is_extremum( IplImage*** dog_pyr, int octv, int intvl, int r, int c )
{
double val = pixval32f( dog_pyr[octv][intvl], r, c );
int i, j, k;
/* check for maximum */
if( val > 0 )
{
for( i = -1; i <= 1; i++ )
for( j = -1; j <= 1; j++ )
for( k = -1; k <= 1; k++ )
if( val < pixval32f( dog_pyr[octv][intvl+i], r + j, c + k ) )
return 0;
}
/* check for minimum */
else
{
for( i = -1; i <= 1; i++ )
for( j = -1; j <= 1; j++ )
for( k = -1; k <= 1; k++ )
if( val > pixval32f( dog_pyr[octv][intvl+i], r + j, c + k ) )
return 0;
}
return 1;
}4.2
準確定位特徵點
以上的極值點搜尋是在離散空間進行的,極值點不真正意義上的極值點。通過對空間尺度函式擬合,可以得到亞畫素級畫素點座標。 尺度空間的Taylor展開式: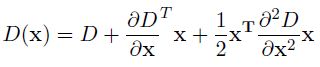 ,其中
,其中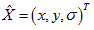 求導並令其為0,得到亞畫素級:
求導並令其為0,得到亞畫素級:
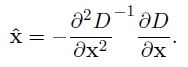 對應的函式值為:
對應的函式值為:
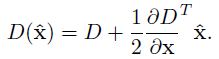
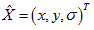 是一個三維向量,向量在任何一個方向上的偏移量大於0.5時,意味著已經偏離了原畫素點,這樣的特徵座標位置需要更新或者繼續插值計算。演算法實現過程中,為了保證插值能夠收斂,設定了最大插值次數(lowe 設定了5次)。同時當
是一個三維向量,向量在任何一個方向上的偏移量大於0.5時,意味著已經偏離了原畫素點,這樣的特徵座標位置需要更新或者繼續插值計算。演算法實現過程中,為了保證插值能夠收斂,設定了最大插值次數(lowe 設定了5次)。同時當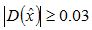 時(本文閾值採用了0.04/S)
,特徵點才被保留,因為響應值過小的點,容易受噪聲的干擾而不穩定。
時(本文閾值採用了0.04/S)
,特徵點才被保留,因為響應值過小的點,容易受噪聲的干擾而不穩定。對離散空間進行函式擬合(插值):
/*
Performs one step of extremum interpolation. Based on Eqn. (3) in Lowe's
paper.
r,c 為特徵點位置,xi,xr,xc,儲存三個方向的偏移量
*/
static void interp_step( IplImage*** dog_pyr, int octv, int intvl, int r, int c,
double* xi, double* xr, double* xc )
{
CvMat* dD, * H, * H_inv, X;
double x[3] = { 0 };
dD = deriv_3D( dog_pyr, octv, intvl, r, c ); //計算三個方向的梯度
H = hessian_3D( dog_pyr, octv, intvl, r, c ); // 計算3維空間的hessian矩陣
H_inv = cvCreateMat( 3, 3, CV_64FC1 );
cvInvert( H, H_inv, CV_SVD ); //計算逆矩陣
cvInitMatHeader( &X, 3, 1, CV_64FC1, x, CV_AUTOSTEP );
cvGEMM( H_inv, dD, -1, NULL, 0, &X, 0 ); //廣義乘法
cvReleaseMat( &dD );
cvReleaseMat( &H );
cvReleaseMat( &H_inv );
*xi = x[2];
*xr = x[1];
*xc = x[0];
}/*
Interpolates a scale-space extremum's location and scale to subpixel
accuracy to form an image feature.
*/
static struct feature* interp_extremum( IplImage*** dog_pyr, int octv, //通過擬合求取準確的特徵點位置
int intvl, int r, int c, int intvls,
double contr_thr )
{
struct feature* feat;
struct detection_data* ddata;
double xi, xr, xc, contr;
int i = 0;
while( i < SIFT_MAX_INTERP_STEPS ) //在最大迭代次數範圍內進行
{
interp_step( dog_pyr, octv, intvl, r, c, &xi, &xr, &xc ); //插值後得到的三個方向的偏移量(xi,xr,xc)
if( ABS( xi ) < 0.5 && ABS( xr ) < 0.5 && ABS( xc ) < 0.5 )
break;
c += cvRound( xc ); //更新位置
r += cvRound( xr );
intvl += cvRound( xi );
if( intvl < 1 ||
intvl > intvls ||
c < SIFT_IMG_BORDER ||
r < SIFT_IMG_BORDER ||
c >= dog_pyr[octv][0]->width - SIFT_IMG_BORDER ||
r >= dog_pyr[octv][0]->height - SIFT_IMG_BORDER )
{
return NULL;
}
i++;
}
/* ensure convergence of interpolation */
if( i >= SIFT_MAX_INTERP_STEPS )
return NULL;
contr = interp_contr( dog_pyr, octv, intvl, r, c, xi, xr, xc ); //計算插值後對應的函式值
if( ABS( contr ) < contr_thr / intvls ) //小於閾值(0.04/S)的點,則丟棄
return NULL;
feat = new_feature();
ddata = feat_detection_data( feat );
feat->img_pt.x = feat->x = ( c + xc ) * pow( 2.0, octv ); // 計算特徵點根據降取樣的次數對應於原圖中位置
feat->img_pt.y = feat->y = ( r + xr ) * pow( 2.0, octv );
ddata->r = r; // 在本尺度內的座標位置
ddata->c = c;
ddata->octv = octv; //組資訊
ddata->intvl = intvl; // 層資訊
ddata->subintvl = xi; // 層方向的偏移量
return feat;
}4.3
刪除邊緣效應
為了得到穩定的特徵點,要刪除掉落在影象邊緣上的點。一個落在邊緣上的點,可以根據主曲率計算判斷。主曲率可以通過2維的 Hessian矩陣求出;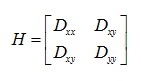
在邊緣上的點,必定使得Hessian矩陣的兩個特徵值相差比較大,而特徵值與矩陣元素有以下關係;
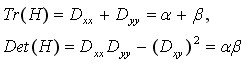
令α=rβ ,所以有:
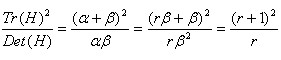
我們可以判斷上述公式的比值大小,大於閾值(lowe採用 r =10)的點排除。
static int is_too_edge_like( IplImage* dog_img, int r, int c, int curv_thr )
{
double d, dxx, dyy, dxy, tr, det;
/* principal curvatures are computed using the trace and det of Hessian */
d = pixval32f(dog_img, r, c); //計算Hessian 矩陣內的4個元素值
dxx = pixval32f( dog_img, r, c+1 ) + pixval32f( dog_img, r, c-1 ) - 2 * d;
dyy = pixval32f( dog_img, r+1, c ) + pixval32f( dog_img, r-1, c ) - 2 * d;
dxy = ( pixval32f(dog_img, r+1, c+1) - pixval32f(dog_img, r+1, c-1) -
pixval32f(dog_img, r-1, c+1) + pixval32f(dog_img, r-1, c-1) ) / 4.0;
tr = dxx + dyy; //矩陣的跡
det = dxx * dyy - dxy * dxy; //矩陣的值
/* negative determinant -> curvatures have different signs; reject feature */
if( det <= 0 ) // 矩陣值為負值,說明曲率有不同符號,丟棄
return 1;
if( tr * tr / det < ( curv_thr + 1.0 )*( curv_thr + 1.0 ) / curv_thr ) //比值小於閾值的特徵點被保留 curv_thr = 10
return 0;
return 1;
}5.計算特徵點對應的尺度
static void calc_feature_scales( CvSeq* features, double sigma, int intvls )
{
struct feature* feat;
struct detection_data* ddata;
double intvl;
int i, n;
n = features->total;
for( i = 0; i < n; i++ )
{
feat = CV_GET_SEQ_ELEM( struct feature, features, i );
ddata = feat_detection_data( feat );
intvl = ddata->intvl + ddata->subintvl;
feat->scl = sigma * pow( 2.0, ddata->octv + intvl / intvls ); // feat->scl 儲存特徵點在總體上尺度
ddata->scl_octv = sigma * pow( 2.0, intvl / intvls ); // feat->feature_data->scl__octv 儲存特徵點在組內的尺度,用來下面計算方向角
}
}6.為特徵點分配方向角
這部分包括:計算鄰域內梯度直方圖,平滑直方圖,複製特徵點(有輔方向的特徵點)static void calc_feature_oris( CvSeq* features, IplImage*** gauss_pyr )
{
struct feature* feat;
struct detection_data* ddata;
double* hist;
double omax;
int i, j, n = features->total;
for( i = 0; i < n; i++ )
{
feat = malloc( sizeof( struct feature ) );
cvSeqPopFront( features, feat );
ddata = feat_detection_data( feat );
hist = ori_hist( gauss_pyr[ddata->octv][ddata->intvl], // 計算鄰域內的梯度直方圖,鄰域半徑radius = 3*1.5*sigma; 高斯加權係數= 1.5 *sigma
ddata->r, ddata->c, SIFT_ORI_HIST_BINS,
cvRound( SIFT_ORI_RADIUS * ddata->scl_octv ),
SIFT_ORI_SIG_FCTR * ddata->scl_octv );
for( j = 0; j < SIFT_ORI_SMOOTH_PASSES; j++ )
smooth_ori_hist( hist, SIFT_ORI_HIST_BINS ); // 對直方圖平滑
omax = dominant_ori( hist, SIFT_ORI_HIST_BINS ); // 返回直方圖的主方向
add_good_ori_features( features, hist, SIFT_ORI_HIST_BINS,//大於主方向的80%為輔方向
omax * SIFT_ORI_PEAK_RATIO, feat );
free( ddata );
free( feat );
free( hist );
}
}6.1
建立特徵點鄰域內的直方圖
上一步scl_octv儲存了每個特徵點所在的組內尺度,下面計算特徵點所在尺度內的高斯影象,以3×1.5×scl_octv為半徑的區域內的所有畫素點的梯度幅值與幅角; 計算公式: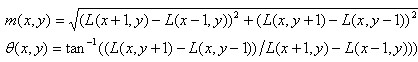
在計算完所有特徵點的幅值與幅角後,使用直方圖統計。直方圖橫軸為梯度方向角,縱軸為對應幅值的累加值(與權重),梯度方向範圍為0~360度,劃分為36個bin,每個bin的寬度為10。 下圖描述的劃分為8個bin,每個bin的寬度為45的效果圖:
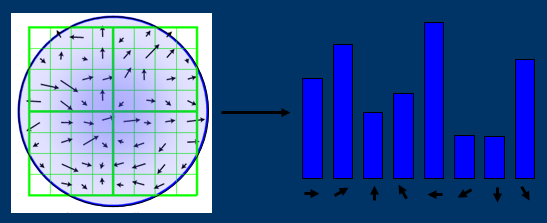
其次,每個被加入直方圖的幅值,要進行權重處理,權重也是採用高斯加權函式,其中高斯係數為1.5×scl_octv。通過高斯加權使特徵點附近的點有較大的權重,可以彌補部分因沒有仿射不變性而產生的不穩定問題; 即每個bin值按下面的公式累加,mag是幅值,後面為權重;i,j,為偏離特徵點距離:
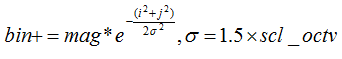
☆程式上可以幫助你理解上面的概念:
static double* ori_hist( IplImage* img, int r, int c, int n, int rad,
double sigma )
{
double* hist;
double mag, ori, w, exp_denom, PI2 = CV_PI * 2.0;
int bin, i, j;
hist = calloc( n, sizeof( double ) );
exp_denom = 2.0 * sigma * sigma;
for( i = -rad; i <= rad; i++ )
for( j = -rad; j <= rad; j++ )
if( calc_grad_mag_ori( img, r + i, c + j, &mag, &ori ) ) //計算領域畫素點的梯度幅值mag與方向ori
{
w = exp( -( i*i + j*j ) / exp_denom ); //高斯權重
bin = cvRound( n * ( ori + CV_PI ) / PI2 );
bin = ( bin < n )? bin : 0;
hist[bin] += w * mag; //直方圖上累加
}
return hist; //返回累加完成的直方圖
}平滑直方圖
lowe建議對直方圖進行平滑,減少突變的影響。static void smooth_ori_hist( double* hist, int n )
{
double prev, tmp, h0 = hist[0];
int i;
prev = hist[n-1];
for( i = 0; i < n; i++ )
{
tmp = hist[i];
hist[i] = 0.25 * prev + 0.5 * hist[i] +
0.25 * ( ( i+1 == n )? h0 : hist[i+1] );
prev = tmp;
}
}複製特徵點
在上面的直方圖上,我們已經找到了特徵點主方向的峰值omax,當存在另一個大於主峰值80%的峰值時,將這個方向作為特徵點的輔方向,即一個特徵點有多個方向,這可以增強匹配的魯棒性。在演算法上,即把該特徵點複製多份作為新的特徵點,新特徵點的方向為這些輔方向,其他屬性保持一致。static void add_good_ori_features( CvSeq* features, double* hist, int n,
double mag_thr, struct feature* feat )
{
struct feature* new_feat;
double bin, PI2 = CV_PI * 2.0;
int l, r, i;
for( i = 0; i < n; i++ ) //檢查所有的方向
{
l = ( i == 0 )? n - 1 : i-1;
r = ( i + 1 ) % n;
if( hist[i] > hist[l] && hist[i] > hist[r] && hist[i] >= mag_thr ) //判斷是不是幅方向
{
bin = i + interp_hist_peak( hist[l], hist[i], hist[r] ); //插值離散處理,取得更精確的方向
bin = ( bin < 0 )? n + bin : ( bin >= n )? bin - n : bin;
new_feat = clone_feature( feat ); //複製特徵點
new_feat->ori = ( ( PI2 * bin ) / n ) - CV_PI;// 為特徵點方向賦值[-180,180]
cvSeqPush( features, new_feat ); //
free( new_feat );
}
}
}7.構建特徵描述子
目前每個特徵點具有屬性有位置、方向、尺度三個資訊,現在要用一個向量去描述這個特徵點,使其具有高度的唯一特徵性。 1.lowe採用了把特徵點鄰域劃分成 d×d (lowe建議d=4) 個子區域,然後再統計每個子區域的方向直方圖(8個方向),直方圖橫軸有8個bin,縱軸為梯度幅值(×權重)的累加。這樣描述這個特徵點的向量為4×4×8=128維。每個子區域的寬度建議為3×octv,octv為組內的尺度。考慮到插值問題,特徵點的鄰域範圍邊長為3×octv×(d+1),考慮到旋轉問題,鄰域的範圍邊長為3×octv×(d+1)×sqrt(2),最後半徑為: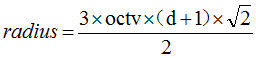
2.把座標系旋轉到主方向位置,再次統計鄰域內所有畫素點的梯度幅值與方向,計算所在子區域,並把幅值×權重累加到這個子區域的直方圖上。 演算法上即統計每個鄰域的方向直方圖時,全部是相對於這個特徵點的主方向的方向。如果主方向為30度,某個畫素點的梯度方向為50度,這時統計到該子區域直方圖上就成了20度。同時由於旋轉,這時權重也必須是按旋轉後的座標。
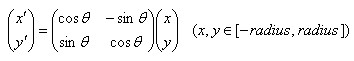
計算所在的子區域的位置:
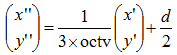
權重按高斯加權函式,係數為描述子寬度的一半,即0.5d:
static double*** descr_hist( IplImage* img, int r, int c, double ori,
double scl, int d, int n )
{
double*** hist;
double cos_t, sin_t, hist_width, exp_denom, r_rot, c_rot, grad_mag,
grad_ori, w, rbin, cbin, obin, bins_per_rad, PI2 = 2.0 * CV_PI;
int radius, i, j;
hist = calloc( d, sizeof( double** ) );
for( i = 0; i < d; i++ )
{
hist[i] = calloc( d, sizeof( double* ) );
for( j = 0; j < d; j++ )
hist[i][j] = calloc( n, sizeof( double ) );
}
cos_t = cos( ori );
sin_t = sin( ori );
bins_per_rad = n / PI2;
exp_denom = d * d * 0.5;
hist_width = SIFT_DESCR_SCL_FCTR * scl;
radius = hist_width * sqrt(2) * ( d + 1.0 ) * 0.5 + 0.5; //計算鄰域範圍半徑,+0.5為了取得更多元素
for( i = -radius; i <= radius; i++ )
for( j = -radius; j <= radius; j++ )
{
/*
Calculate sample's histogram array coords rotated relative to ori.
Subtract 0.5 so samples that fall e.g. in the center of row 1 (i.e.
r_rot = 1.5) have full weight placed in row 1 after interpolation.
*/
c_rot = ( j * cos_t - i * sin_t ) / hist_width; //
r_rot = ( j * sin_t + i * cos_t ) / hist_width;
rbin = r_rot + d / 2 - 0.5; //旋轉後對應的x``及y''
cbin = c_rot + d / 2 - 0.5;
if( rbin > -1.0 && rbin < d && cbin > -1.0 && cbin < d )
if( calc_grad_mag_ori( img, r + i, c + j, &grad_mag, &grad_ori )) //計算每一個畫素點的梯度方向、幅值、
{
grad_ori -= ori; //每個畫素點相對於特徵點的梯度方向
while( grad_ori < 0.0 )
grad_ori += PI2;
while( grad_ori >= PI2 )
grad_ori -= PI2;
obin = grad_ori * bins_per_rad; //畫素梯度方向轉換成8個方向
w = exp( -(c_rot * c_rot + r_rot * r_rot) / exp_denom ); //每個子區域內畫素點,對應的權重
interp_hist_entry( hist, rbin, cbin, obin, grad_mag * w, d, n ); //為了減小突變影響對附近三個bin值三線性插值處理
}
}
return hist;
}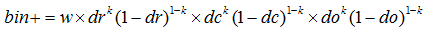 ,這就是128維向量的資料,計算方法
,這就是128維向量的資料,計算方法static void interp_hist_entry( double*** hist, double rbin, double cbin,
double obin, double mag, int d, int n )
{
double d_r, d_c, d_o, v_r, v_c, v_o;
double** row, * h;
int r0, c0, o0, rb, cb, ob, r, c, o;
r0 = cvFloor( rbin );
c0 = cvFloor( cbin );
o0 = cvFloor( obin );
d_r = rbin - r0;
d_c = cbin - c0;
d_o = obin - o0;
/*
The entry is distributed into up to 8 bins. Each entry into a bin
is multiplied by a weight of 1 - d for each dimension, where d is the
distance from the center value of the bin measured in bin units.
*/
for( r = 0; r <= 1; r++ )
{
rb = r0 + r;
if( rb >= 0 && rb < d )
{
v_r = mag * ( ( r == 0 )? 1.0 - d_r : d_r );
row = hist[rb];
for( c = 0; c <= 1; c++ )
{
cb = c0 + c;
if( cb >= 0 && cb < d )
{
v_c = v_r * ( ( c == 0 )? 1.0 - d_c : d_c );
h = row[cb];
for( o = 0; o <= 1; o++ )
{
ob = ( o0 + o ) % n;
v_o = v_c * ( ( o == 0 )? 1.0 - d_o : d_o );
h[ob] += v_o;
}
}
}
}
}
}static void hist_to_descr( double*** hist, int d, int n, struct feature* feat )
{
int int_val, i, r, c, o, k = 0;
for( r = 0; r < d; r++ )
for( c = 0; c < d; c++ )
for( o = 0; o < n; o++ )
feat->descr[k++] = hist[r][c][o];
feat->d = k;
normalize_descr( feat ); //向量歸一化
for( i = 0; i < k; i++ )
if( feat->descr[i] > SIFT_DESCR_MAG_THR ) //設定門限,門限為0.2
feat->descr[i] = SIFT_DESCR_MAG_THR;
normalize_descr( feat ); //向量歸一化
/* convert floating-point descriptor to integer valued descriptor */
for( i = 0; i < k; i++ ) //換成整形值
{
int_val = SIFT_INT_DESCR_FCTR * feat->descr[i];
feat->descr[i] = MIN( 255, int_val );
}
}最後對特徵點按尺度大小進行排序,強特徵點放在前面; 這樣每個特徵點就對應一個128維的向量,接下來可以用可以用向量做以後的匹配工作了。 特徵點匹配原理後序文章會更新~
------------------------------------------------------------------------------------
在此非常感謝CSDN上幾位影象上的大牛,我也是通過他們的文章去學習研究的,本文也是參考了他們的文章才寫成!
推薦看大牛們的文章,原理寫的很好!
http://blog.csdn.net/abcjennifer/article/details/7639681
http://blog.csdn.net/zddblog/article/details/7521424
http://blog.csdn.net/chen825919148/article/details/7685952
http://blog.csdn.net/xiaowei_cqu/article/details/8069548
相關推薦
【特徵匹配】SIFT原理與C原始碼剖析
SIFT的原理已經有很多大牛的部落格上做了解析,本文重點將以Rob Hess等人用C實現的程式碼做解析,結合程式碼SIFT原理會更容易理解。一些難理解點的用了☆標註。 歡迎大家批評指正! 轉載請註明出處:http://blog.csdn.net/l
【特徵匹配】ORB原理與原始碼解析
相關 : CSDN-勿在浮沙築高臺 為了滿足實時性的要求,前面文章中介紹過快速提取特徵點演算法Fast,以及特徵描述子Brief。本篇文章介紹的ORB演算法結合了Fast和Brief的速度優勢,並做了改進,且ORB是免費。 Ethan Rublee等人2011年
【特徵匹配】RANSAC演算法原理與原始碼解析
轉載請註明出處:http://blog.csdn.net/luoshixian099/article/details/50217655 勿在浮沙築高臺 隨機抽樣一致性(RANSAC)演算法,可以在一組包含“外點”的資料集中,採用不斷迭代的方法,尋找最優引數模型,不符合最
【特徵匹配】Harris及Shi-Tomasi原理及原始碼解析
演算法原理:呼叫cornerMinEigenVal()函式求出每個畫素點自適應矩陣M的較小特徵值,儲存在矩陣eig中,然後找到矩陣eig中最大的畫素值記為maxVal,然後閾值處理,小於qualityLevel*maxVal的特徵值排除掉,最後函式確保所有發現的角點之間具有足夠的距離。void cv::goo
【特徵匹配】BRIEF特徵描述子原理及原始碼解析
轉載請註明出處: http://blog.csdn.net/luoshixian099/article/details/48338273 傳統的特徵點描述子如SIFT,SURF描述子,每個特徵點採用128維(SIFT)或者64維(SURF)向量去描述,每個維度上
【分治法】合併排序及C++原始碼
(1)合併排序是成功應用分治技術的一個完美例子。 對於一個需要排列的陣列A[0..n-1],合併排序將它一分為二:A[0..[n/2]-1]和A[[n/2]..n-1],並對每個子陣列遞迴排序,然後把這個排好序的子數組合併為一個有序陣列。 Mergeso
【影象特徵提取13】SIFT原理之KD樹+BBF演算法解析
本文轉載自:http://blog.csdn.NET/luoshixian099/article/details/47606159 繼上一篇中已經介紹了,最後得到了一系列特徵點,每個特徵點對應一個128維向量。假如現在有兩副圖片都已經提取到特徵點,現在要做
MySQL數據庫學習【第九篇】索引原理與慢查詢優化
xxx 結構 復合 unix select查詢 全文搜索 等等 學習 獲取數據 一、介紹 1.什麽是索引? 一般的應用系統,讀寫比例在10:1左右,而且插入操作和一般的更新操作很少出現性能問題,在生產環境中,我們遇到最多的,也是最容易出問題的,還是一些復雜的查詢操作,因此對
【C/C++】extern 關鍵字與 C/C++ 混合程式設計
extern 是一個名字修飾約定。 所謂名字修飾約定,就是指變數名、函式名等經過編譯後重新輸出名稱的規則。 C++支援函式過載,而C不支援,兩者的編譯規則也不一樣。函式被C++編譯後在符號庫中的名字與C語言的不 同。例如,假設某個函式的原型為:void fo
【持久化框架】Mybatis簡介與原理
什麼是Mybatis MyBatis 本是apache的一個開源專案iBatis, 2010年這個專案由apache software foundation 遷移到了google code,並且改名為MyBatis 。iBATIS一詞來源於“internet
【Spring原始碼閱讀】BeanDefinition原理與載入流程
BeanDefinition介面定義及其相關子類實現 在Spring容器初始化過程中,Spring會將配置檔案中配置的Java類封裝成一個個BeanDefinition。 BeanDefinition儲存了具體代表Bean的類,並通過實現了AttributeAccessor介面定義了
【kubernetes/k8s概念】istio 原理與架構
看著有點蒙,摘錄一下,待有時間分析原始碼 WHY Istio 當應用被拆分為多個微服務後,程序內的方法呼叫變成了程序間的遠端呼叫。引入了對大量服務的連線、管理和監控的複雜性。隨著微服務出現,微服務的連線、管理和監控成為難題
【特徵工程】2 機器學習中的資料清洗與特徵處理綜述
背景 隨著美團交易規模的逐步增大,積累下來的業務資料和交易資料越來越多,這些資料是美團做為一個團購平臺最寶貴的財富。通過對這些資料的分析和挖掘,不僅能給美團業務發展方向提供決策支援,也為業務的迭代指明瞭方向。目前在美團的團購系統中大量地應用到了機器學習和資料探勘技術,例
藍橋杯 2017 國賽B組C/C++【對局匹配】
題意就是給我們一串數 讓我們儘可能地取 約束條件是a[i] 和a[i]+k不能同時出現 所有元素之間相差k的元素都不能同時出現 讓我們求所能取到的最大的數的和是多少分析: dp思路,這個和樹形dp有點相似 就是列舉0~k 然後在每個這個元素上迭代加k 每個元素儲存兩個狀態
【C/C++開發】【VS開發】win32位與x64位下各型別長度對比
64 位的優點:64 位的應用程式可以直接訪問 4EB 的記憶體和檔案大小最大達到4 EB(2 的 63 次冪);可以訪問大型資料庫。本文介紹的是64位下C語言開發程式注意事項。 1. 32 位和 64 位C資料型別 32和64位C語言內建資料型別,如下表所示:
【特徵工程】3 特徵工程技術與方法
引言 在之前學習機器學習技術中,很少關注特徵工程(Feature Engineering),然而,單純學習機器學習的演算法流程,可能仍然不會使用這些演算法,尤其是應用到實際問題的時候,常常不知道怎麼提取特徵來建模。 特徵是機器學習系統的原材料,對最終模型的影響是毋庸置疑的。 特徵工程的重要意義 資
【微信小程式】的原理與許可權
這幾天圈子裡到處都在傳播著這樣一個東西,微信公眾平臺提供了一種新的開放能力,開發者可以快速開發一個小程式,取名曰:微信公眾平臺-小程式 據說取代移動開發安卓和蘋果,那這個東東究竟是幹嗎用的?但很多人覺得是網頁版應用。 有的人很雞凍,但是……最後文章會提及具體的許可權開放問題,所以,還是保持
【目標檢測】SIFT特徵學習記錄
一、生成尺度空間 尺度空間定義為 其中I(x,y)是輸入影象,*是卷積運算,可變尺度的高斯函式 二維高斯函式畫出來是下面這樣的, 卷積過程是在影象上進行滑窗,核函式和影象點乘相加。 1.1 建立高斯金字塔LOG 首先對影象做降取樣,根據不同的降
【特徵工程】一種異常值檢測方法、原理、程式碼實現 (基於箱線圖)
先介紹使用到的方法原理,也就是一種異常檢測的方法。 首先要先了解箱線圖。 箱線圖 箱線圖(Boxplot)也稱箱須圖(Box-whisker Plot),是利用資料中的五個統計量:最小值、第一四分位數、中位數、第三四分位數與最大值來描述資料的一種方法,它也可以
移動開發之【微信小程式】的原理與許可權問題以及相關的簡易教程
這幾天圈子裡到處都在傳播著這樣一個東西,微信公眾平臺提供了一種新的開放能力,開發者可以快速開發一個小程式,取名曰:微信公眾平臺-小程式 據說取代移動開發安卓和蘋果,那這個東東究竟是幹嗎用的?但很多人覺得是網頁版應用。有的人很雞凍,但是……最後文章會提及具體的許


