一、生成尺度空間

尺度空間定義為

其中I(x,y)是輸入影象，*是卷積運算，可變尺度的高斯函式

二維高斯函式畫出來是下面這樣的，

卷積過程是在影象上進行滑窗，核函式和影象點乘相加。

1.1 建立高斯金字塔LOG

首先對影象做降取樣，根據不同的降取樣尺度，可以生成多層影象，每層影象再用不同尺度的高斯核進行平滑，每一層又能得到多組不同模糊程度的影象。

1.2 建立高斯差分金字塔DOG

為了在尺度空間更高效的檢測穩定的關鍵點，定義

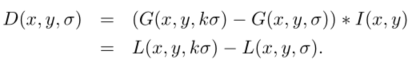
同層內相鄰兩組影象做差分。

相鄰兩層之間的尺度相差一個比例因子k。如果每組有S層，則。上一組影象的最底層影象是由下一組中尺度為2σ的影象進行降取樣得到的。

二、檢測區域性空間極值點

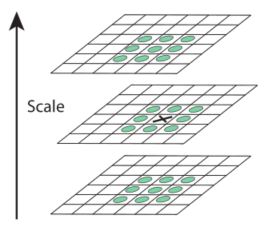
尋找極值點時，每個畫素要和本層影象相鄰的畫素和相鄰層的相鄰畫素點進行比較，只有它大於（或小於）所有相鄰點時，才判定為極值點。

如下圖所示，中間的檢測點要和其所在影象的3×3鄰域8個畫素點，以及其相鄰的上下兩層的3×3領域18個畫素點，共26個畫素點進行比較。

三、精確定位極值點

3.1 剔除低對比度極值點

將做泰勒展開，

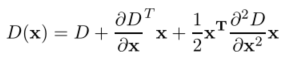
其中，

極值點如下，

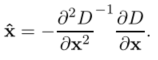
把極值點帶人泰勒展開式中，得到

作者在論文中設定閾值條件，小於0.03的極值點將被剔除。

3.2 剔除邊緣極值點

光是剔除掉低對比度的極值點還是不夠的，DOG會在邊緣處產生較強的響應，但這些偽極值點並不是我們想要的。

在邊緣梯度的方向上主曲率值比較大，而沿著邊緣方向則主曲率值較小。候選特徵點的DoG函式的主曲率可以通過2x2的Hessian矩陣H計算，

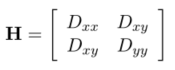
主曲率與H的特徵值成比例關係。假設為H的最大特徵值，為H的最小特徵值，則

其中，Tr(H)為矩陣H的跡，Det(H)為矩陣H的行列式。

設γ=α/β表示最大特徵值和最小特徵值的比值，則

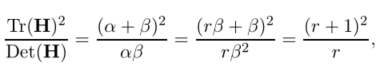
這樣，上式只與兩個特徵值的比例有關，與具體的值無關。

檢測主曲率是否小於閾值r，只需判斷

論文中設定r=10。

四、方向賦值

通過尺度不變性就極值，可以使其具有方向不變性。利用關鍵點鄰域畫素的梯度方向分佈特性，可以為每個關鍵點指定方向，使其具有旋轉不變性。

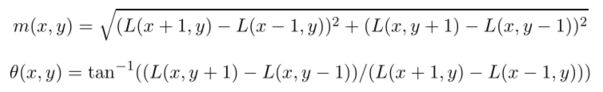
計算出梯度的幅值和方向之後，就可以用直方圖統計特徵點鄰域內畫素的梯度幅值和方向了。360°分成36個直方圖的柱，橫軸是方向，縱軸是幅值的累加，在直方圖的峰值就是特徵點的主方向。在梯度直方圖中，當存在一個相當於主峰值80%能量的柱值時，則可以將這個方向認為是該特徵點輔助方向。直方圖的統計半徑為3×1.5σ。作者指出15%的關鍵點具有多方向，而且這些點對匹配的穩定性很關鍵。最終，關鍵點的方向可以由和主峰值最近的三個柱值通過拋物線插值得到。

五、影象描述子

前面已經為每個關鍵點賦予了位置、尺度和方向資訊。接下來需要用一組向量來描述關鍵點。

如下圖所示，

關鍵點附近劃分為2x2個子區域，每個子區域有8個方向的資訊，一個SIFT向量就是2x2x8=32維。

作者指出在實驗中4x4x8=128維的描述子表現最好。