DFS應用——找出無向圖的割點
【0】README
0.1) 本文總結於 資料結構與演算法分析, 原始碼均為原創, 旨在 理解 “DFS應用於找割點” 的idea 並用原始碼加以實現;
0.2) 必須要事先 做個specification的是:對於給定圖的除開起始vertex的那些 vertexes,都可以通過我們的 rules(見下文)找出割點,即對於根(start),我們需要做個special 的test,參見main函式中最後的原始碼;
【1】 無向圖割點相關
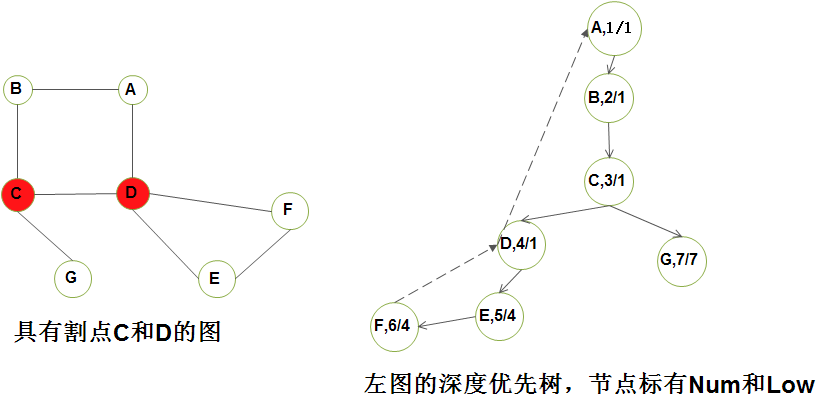
1.1)割點定義(articulate point): 如果一個圖不是雙連通的, 那麼將其刪除後圖將不再連通的那些頂點叫做割點;
1.2)雙連通性定義:
1.3)看個荔枝: 如果節點是 路由器或者交換機 的話, 邊是網路鏈路, 那麼若有一臺 路由器或者交換機 出故障而不能執行, 則網路並不會受到影響的;
【2】深度優先搜尋提供一種找出連通圖中的所有割點的線性時間演算法
2.1)首先, 從圖中任一頂點開始, 執行深度優先搜尋並在頂點被訪問時給它們編號, 對於每一個頂點,我們稱其為先序編號 Num(v) (注:在原始碼中,vertexIndex 表示Num的含義,下文不再累述);
2.2)然後, 對於深度優先搜尋生成樹上的每一個頂點v, 計算編號最低的頂點, 我們稱之為 Low(v),該點從v 開始, 通過樹的零條或多條邊且可能還有一條背向邊而達到 (注:在原始碼中,vertexLow 表示Low的含義,下文不再累述)
Attention)右上圖中的深度優先搜尋樹首先指出先序編號,然後指出上述法則下可達到的最低編號頂點;
2.3)從A、B、C開始的可達到最低編號頂點為1(A), 因為它們都能夠通過樹的邊到D, 然後再由一條背向邊回到A;
2.4)我們可以通過對該深度優先生成樹執行一次後序遍歷有效地算出 Low, 根據low的定義,可知Low(v)是:
- (1) Num(v) +
- (2) 所有背向邊(v, w)中的最低Num(w) +
- (3) 樹的所有邊(v, w)中的最低Low(w), 以上三者中 的最小者;
- 對以上規則的分析: 第一個條件是不選取邊; 第二種方法是不選取樹的邊 而是選取一條背向邊;第三種方法則是選擇樹的某些邊以及可能還有一條背向邊;
Attention)
- A1)由於我們需要對v 的所有兒子計算出 Low 值後才能計算Low(v) , 因此這是一個後序遍歷;
- A2)對於任一條邊(v, w), 我們只要檢查Num(v)和 Num(w)就可以知道它是樹的一條邊還是一條背向邊(因為如果是深度優先樹的邊, Num(v) < Num(w), 因為v比w先被訪問到, 而如果是背向邊,Num(v) >Num(w)的 );
- A3)因此, Low(v) 容易計算: 我們僅僅需要掃描v 的鄰接表,應用適當 的法則,並記住最小值。 所有的計算花費 O(|E| + |V|);
【3】剩下要做的就是利用 這些資訊找出所有的割點。
3.1)對於根(見本文README部分):根是割點當且僅當它有多於一個的兒子(根至少要有兩個兒子),因為如果它有兩個兒子, 那麼刪除根則使得節點不連通而分佈在不同的子樹上;如果根只有一個兒子, 那麼除去該根只不過是斷離該根。
3.2)對於任何其他頂點v: 它是割點當且僅當它有某個兒子w 使得Low(w)>= Num(v); (注意, 這個條件在根處總是滿足的; 因此,需要進行特別的測試)(乾貨)
【4】source code + printing results
- 4.2.1) 找割點的函式
// "find the articulation point from the given graph"
void findArticulate(Vertex vertex, int depth)
{
int i;
AdjTable temp;
Vertex adjVertex;
visited[vertex] = 1; // update visited status of vertex
vertexIndex[vertex] = counter++; // evaluating vertex index with counter
vertexLow[vertex] = vertexIndex[vertex]; // the 1st rule: evaluating vertex low with counter
temp = adj[vertex];
while(temp->next)
{
adjVertex = temp->next->vertex;
if(visited[adjVertex]) // judge whether the adjVertes was visited before
{
if(vertexIndex[vertex] > vertexIndex[adjVertex] && parent[vertex] != adjVertex)
{
//parent[adjVertex] = vertex; // building back side, attention of condition of building back side above
//ex vertex= 3, adjVertex = 0
// just for printing effect
for(i = 0; i < depth; i++)
printf(" ");
printf("vertex[%c]->vertex[%c] (backside) \n", flag[vertex], flag[adjVertex]);
// only if there's a backside, we apply the 2rd rule into the graph
vertexLow[vertex] = minimum(vertexLow[vertex], vertexIndex[adjVertex]); // the 2rd rule: find lowest vertexIndex[w] among all edges(v, w)
}
}
// if(!visited[adjVertex])
// there's the case no backside, and if condition sentences refers to case of backside
else
{
parent[adjVertex] = vertex;
// just for printing effect
for(i = 0; i < depth; i++)
printf(" ");
printf("vertex[%c]->vertex[%c] (building edge)\n", flag[vertex], flag[adjVertex]);
findArticulate(adjVertex, depth+1);
if(vertex != start) // judge whether the vertex is the start (root) or not
if(vertexLow[adjVertex] >= vertexIndex[vertex])
printf("\n\t vertex[%c] proves to be an articulation point !", flag[vertex]);
vertexLow[vertex] = minimum(vertexLow[vertex], vertexLow[adjVertex]); // the 3rd rule: find lowest verdexLow[w] among all edges(v, w)
}
temp = temp->next;
}
}
- 4.2.2) 判斷start頂點是否是割點的函式
int isStartArticulation()
{
int i;
AdjTable temp;
Vertex adjVertex;
temp = adj[start];
while(temp->next)
{
adjVertex = temp->next->vertex;
if(adjVertex == start)
{
temp = temp->next;
continue;
}
dfs(adjVertex, 1);
for(i=0; i<size; i++)
if(visited[i] != 1) // "refers that the start vertex is the articulation point"
return 1;
temp = temp->next;
}
return 0;
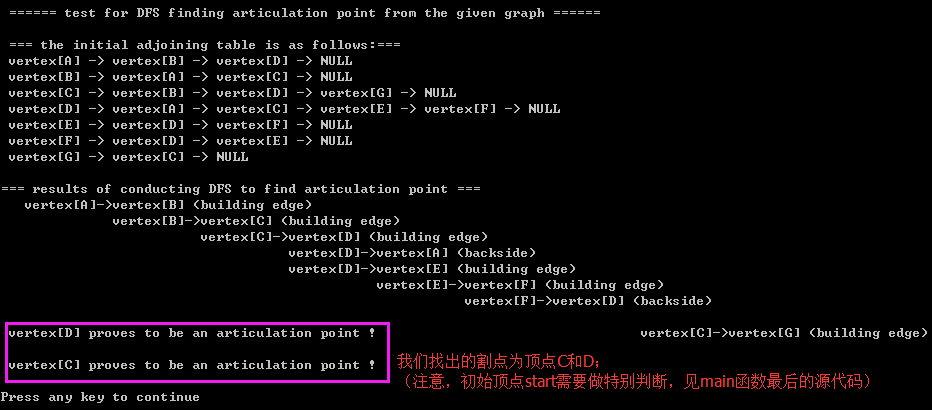
}4.3)printing results:
相關推薦
DFS應用——找出無向圖的割點
【0】README 0.1) 本文總結於 資料結構與演算法分析, 原始碼均為原創, 旨在 理解 “DFS應用於找割點” 的idea 並用原始碼加以實現; 0.2) 必須要事先 做個specification的是:對於給定圖的除開起始vertex的那些 ver
找出無向圖中所有的環的演算法
本文給出了一個找到無向圖中所有的環的遞迴演算法,該演算法是基於DFS(深度優先搜尋)的,大概的思路是:在深度優先搜尋無向圖的過程中,當遇到起始點的時候,會認定為出現環(在本文中只是找出了無向圖中所有的長度大於等於3的環(長度為1和2的環沒有意思),所以在深搜的過程中,當遇到
2018/2/11 每日一學 無向圖割頂和橋
return set else 所有 scanf ear .net 存在 sin 割頂和橋:對於無向圖G,如果刪除某個節點u後,連通分量數目增加,則稱u為圖的割頂;如果刪除某條邊後,連通分量數目增加,則稱該邊為圖的橋。 對於連通圖刪除割頂或橋後都會使得圖不再連通。 我們利用
無向圖割頂與橋
#include<cstdio> #include<cstring> #include<vector> using namespace std; const int maxn=100000+10; int n,m; int dfs_clock;//時鐘,每訪問一個
poj 2117Electricity無向圖割頂
Electricity Time Limit: 5000MS Memory Limit: 65536K Total Submissions: 6405
無向圖求點割集的演算法
http://blog.csdn.net/xinghongduo/article/details/6202646 黑書上給出了關於求點割集的演算法,但是比較模糊,我查閱了網路上的相關資料,理解了求點割集的過程,寫出如下求點割集的程式碼,並寫了一些簡單的證明. 割點集的定
無向圖求點割集演算法
黑書上給出了關於求點割集的演算法,但是比較模糊,我查閱了網路上的相關資料,理解了求點割集的過程,寫出如下求點割集的程式碼,並寫了一些簡單的證明. 割點集的定義:如果在連通圖G中去掉某一點後圖不連通,那麼這個點即為G的割點,所有割點的集合即為點割集。 求點割集的方法:利用
通過DFS和BFS判斷無向圖是否連通
基礎定義 無向圖:沒有方向的圖 連通圖:任意兩個頂點可以直接或者通過其他頂點走通,那麼就是連通圖,和完全圖需要區別(完全圖是需要任意兩個頂點直接有路) 遍歷圖的基本方法來判斷是否連通 DFS和BFS有的步驟都是從一個頂點開始,然後判斷該頂點是否被訪問
Newcoder contest 392 I 逛公園 (無向圖割邊模板)
參觀 mes include 無法 mil 重復 get color bit <題目鏈接> 題目描述: 月月和華華一起去逛公園了。公園很大,為了方便,可以抽象的看成一個N個點M條邊的無向連通圖(點是景點,邊是道路)。公園唯一的入口在1號點,月月和華華要從這裏
hdu4612 無向圖中隨意加入一條邊後使橋的數量最少 / 無向圖縮點+求樹的直徑
child iostream tracking amp min esp _id 矛盾 cstring 題意如上,含有重邊(重邊的話,倆個點就能夠構成了邊雙連通)。 先縮點成樹,在求數的直徑,最遠的連起來,剩下邊(橋)的自然最少。這裏學習了樹的直徑求法:第一次選隨意
無向圖縮點poj3177 Redundant Paths
namespace while paths AI poj AC 新的 所有 mes http://poj.org/problem?id=3177 題意:有n個牧場,互相連通,現在要求使得任意兩個牧場之間至少有兩條道路可走,求至少需要修多少條新的路 -------------
1000E We Need More Bosses(無向圖縮點 + 樹的直徑)
E. We Need More Bosses time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard outp
Tarjan無向圖縮環(求邊雙)/有向圖縮環(求邊雙)/無向圖求點雙
邊雙與點雙 不嚴謹的定義, 邊雙=刪掉一條邊依然連通 點雙=刪掉一個點依然連通 無向圖Tarjan求邊雙 先說無向圖。無向圖就比有向圖簡單一些,因為只有返祖邊而沒有橫叉邊。 用棧來儲存已訪問的點。 如果已經訪問過了,就把它當返祖邊處理(low=min(low,
hdu-4612(無向圖縮點+樹的直徑)
%d include void size can mem col 解題思路 span 題意:給你n個點和m條邊的無向圖,問你如果多加一條邊的話,那麽這個圖最少的橋是什麽 解題思路:無向圖縮點和樹的直徑,用並查集縮點; #include<iostream>
DFS的運用(二分圖判定、無向圖的割頂和橋,雙連通分量,有向圖的強連通分量)
part str stack void div prev this 沒有 2-sat 一、dfs框架: 1 vector<int>G[maxn]; //存圖 2 int vis[maxn]; //節點訪問標記 3 void dfs(int u
poj 1523 求無向圖所有割點以及刪除割點後連通分量個數 給出詳細演算法思路
題意 無向圖找出每個割點,然後求出刪除這個割點所得的連通分量個數 節點編號在1-1000,但沒說按順序給出 思路 無向圖求所有割點是一類經典問題,這篇blog就以這題為例簡單介紹一下求解的演算法思路 我們希望在O(n+m)的時間裡求出所有的割
藍橋杯歷屆試題 危險係數(dfs或者並查集求無向圖關於兩點的割點個數)
Description 抗日戰爭時期,冀中平原的地道戰曾發揮重要作用。 地道的多個站點間有通道連線,形成了龐大的網路。但也有隱患,當敵人發現了某個站點後,其它站點間可能因此會失去聯絡。 我們來定義一個危險係數DF(x,y): 對於兩個站點x和y (x != y), 如果能找到一個站點z,當
深度優先遍歷找出一個無向圖中的環
進行深度優先遍歷的時候,當考察的點的下一個鄰接點是已經被遍歷的點,並且不是自己之前的父親節點的時候,我們就找到了一條逆向邊,因此可以判斷該無向圖中存在環路。 visited陣列記錄了節點的訪問狀態,visited[i] = 0表示節點i尚未被訪問過; visi
hdu 6041 I Curse Myself 無向圖找環+優先隊列
ger update cst scan ges mst des sim search I Curse Myself Time Limit: 8000/4000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/
[HDOJ6081] 度度熊的王國戰略(無向圖最小割,數據水)
eof printf ret pri sin %d logs ems ++ 題目鏈接:http://acm.hdu.edu.cn/showproblem.php?pid=6081 無向圖求割點,應該是個論文題,16年有一篇SW算法+斐波那契堆優化的論文。 但是這數據怎麽這!