第三章 決策樹 3.1決策樹構造
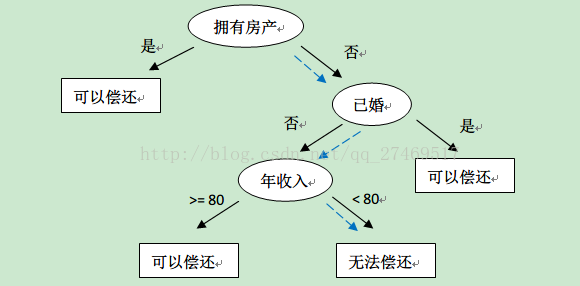
http://cn.akinator.com/ “神燈猜名人”這個遊戲很多人都玩過吧,問很多問題,然後逐步猜測你想的名人是誰。決策樹的工作原理與這個類似,輸入一系列資料,然後給出遊戲答案。決策樹也是最經常使用的資料探勘演算法。書上給了一個流程圖決策樹,很簡單易懂。
這裡,橢圓形就是判斷模組,方塊就是終止模組。kNN 方法也可以完成分類任務,但是缺點是無法給出資料的內在含義。決策樹的主要優勢就在於資料形式容易理解。
==============================================================================
決策樹
優點:計算複雜度不高,輸出結果容易理解,對中間值缺失不敏感,可以處理不相關特徵資料。
缺點:可能會產生過度匹配問題。
適用資料型別:數值型和標稱型。
虛擬碼:
creatBranch():
if so return 類標籤:
else:
尋找劃分資料集的最好特徵
劃分資料集
建立分支節點
for 每個劃分的子集
呼叫函式 creatBranch() 並增加返回結果到分支節點中
return 分支節點可以看出這是一個遞迴函式,在裡面直接呼叫了自己。
==============================================================================
決策樹的一般流程:
- 收集資料:可以使用任何方法
- 準備資料:樹構造演算法只適用於標稱型資料,因此數值型資料必須離散化。
- 分析資料:可以使用任何方法,構造樹完成以後,我們應該檢查圖形是否符合預期。
- 訓練演算法:構造樹的資料結構。
- 測試演算法:使用經驗樹計算錯誤率。
- 使用演算法:此步驟可以適用於任何監督學習演算法,而使用決策樹可以更好地理解資料的內在含義。
一些決策樹演算法採用二分法,我們不用這種方法。我們可能會遇到更多的選項,比如四個,然後創立四個不同分支。本書將使用 ID3 演算法劃分資料集。
==============================================================================
資訊增益:
劃分資料集的大原則是:將無序的資料變得更加有序。
在劃分資料集之前之後資訊發生的變化稱為資訊增益。
集合資訊的度量方式稱為夏農熵或者簡稱為熵。熵定義為資訊的期望值。公式略過不表。
給一段程式碼,計算給定資料集的熵:
# -*- coding:utf-8 -*-
from math import log
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): # 為所有可能分類建立字典
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob *log(prob, 2) # 以 2 為底求對數
return shannonEnt然後自己利用 createDataSet() 函式來得到35頁表 3-1 的魚類鑑定資料集。
def createDataSet():
dataSet = [[1,1,'yes'],
[1,1,'yes'],
[1,0,'no'],
[0,1,'no'],
[0,1,'no']]
labels = ['no surfacing','flippers']
return dataSet, labels最後來執行一下試試,我們建立一個 run_trees.py
# -*- coding:utf-8 -*-
# run_trees.py
import trees
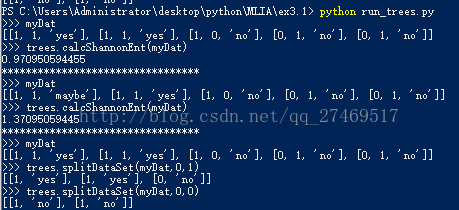
myDat,labels = trees.createDataSet()
print myDat
print trees.calcShannonEnt(myDat)
熵越多高,說明混合資料越多。這裡新增一個 “maybe” 分類,表示可能為魚類。
測試:
# -*- coding:utf-8 -*-
import trees
myDat,labels = trees.createDataSet()
print myDat
print trees.calcShannonEnt(myDat)
print '*********************************'
myDat[0][2] = 'maybe' # 0 指的是dataSet第一個[],-1 指[]裡面倒數第一個元素
print myDat
print trees.calcShannonEnt(myDat)結果:
====================================================================================================
3.1.2 劃分資料集
分類演算法除了需要測量資訊熵,還要劃分資料集。
我們對每個特徵劃分資料集的結果計算一次資訊熵,然後判斷按照哪個特徵劃分資料集是最好的方式。
按照給定特徵劃分資料集,程式碼接著 trees.py 寫:
def splitDataSet(dataSet, axis, value):
retDataSet= [] # 建立新的 list 物件
for featVec in dataSet:
if featVec[axis] == value:
# 抽取
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet注意 append() 和 extend() 的區別:
>>>a = [1,2,3]
>>>b = [4,5,6]
>>>a.append(b)
>>>a
[1,2,3,[4,5,6]] >>>a = [1,2,3]
>>>a.extend(b)
>>>a
[1,2,3,4,5,6]=============================================================================================
現在可以在前面的簡單樣本資料上測試函式 splitDataSet()
在 run_trees.py 裡面加些程式碼:
# -*- coding:utf-8 -*-
# run_trees.py
import trees
myDat,labels = trees.createDataSet()
print '>>> myDat'
print myDat
print '>>> trees.calcShannonEnt(myDat)'
print trees.calcShannonEnt(myDat)
print '*********************************'
myDat[0][2] = 'maybe' # 0 指的是dataSet第一個[],-1 指[]裡面倒數第一個元素
print '>>> myDat'
print myDat
print '>>> trees.calcShannonEnt(myDat)'
print trees.calcShannonEnt(myDat)
print '*********************************'
reload(trees)
myDat,labels = trees.createDataSet()
print '>>> myDat'
print myDat
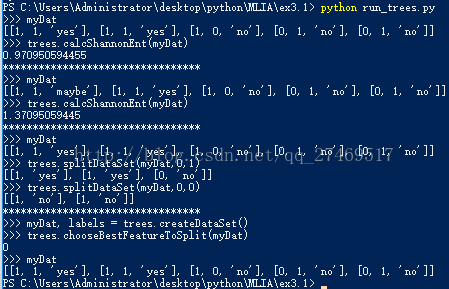
print '>>> trees.splitDataSet(myDat,0,1)'
print trees.splitDataSet(myDat,0,1)
print '>>> trees.splitDataSet(myDat,0,0)'
print trees.splitDataSet(myDat,0,0)
=======================================================================
接下來我們要遍歷整個資料集,迴圈計算夏農熵和 splitDataSet() 函式,找到最好的特徵劃分方式。熵計算將會告訴我們如何劃分資料集是最好的組織方式。
加程式碼:
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0; bestFeature = -1
for i in range(numFeatures): # 遍歷資料集中的所有特徵
# 建立唯一的分類標籤列表
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) # set 是一個集合
newEntropy = 0.0
for value in uniqueVals: # 遍歷當前特徵中的所有唯一屬性值
# 計算每種劃分方式的資訊熵
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet) # 對所有唯一特徵值得到的熵求和
infoGain = baseEntropy - newEntropy
if (infoGain > bestInfoGain):
# 計算最好的收益
bestInfoGain = infoGain
bestFeature = i
return bestFeature這段程式碼就是選取特徵,劃分資料集,計算得出最好的劃分資料集的特徵。
在在 run_trees.py 裡面加些程式碼:
print '*********************************'
reload(trees)
print '>>> myDat, labels = trees.createDataSet()'
myDat, labels = trees.createDataSet()
print '>>> trees.chooseBestFeatureToSplit(myDat)'
print trees.chooseBestFeatureToSplit(myDat)
print '>>> myDat'
print myDat結果如下:
程式碼的意義在於,告訴我們第0個特徵(不浮出水面是否可以生存)是最好的用於劃分資料集的特徵。
如果不相信這個結果,可以修改 calcShannonEnt(dataSet) 函式來測試不同特徵分組的輸出結果。
===============================================================================
3.1.3 遞迴構建決策樹
從資料集構造決策樹演算法所需要的子功能模組,原理如下:得到原始資料集,然後基於最好的屬性值劃分資料集,由於特徵值可能多於兩個,因此可能存在大於兩個分支的資料集劃分。第一次劃分後,資料將被鄉下傳遞到樹分支的下一個節點,在這個節點上,我們可以再次劃分資料。我們可以採用遞迴的原則處理資料集。
在新增程式碼前,在 trees.py 頂部加上一行程式碼:
import operator然後新增:
def majorityCnt(classList):
classCount = {} # 建立鍵值為 classList 中唯一值的資料字典
for vote in classList:
if vote not in classCount.keys():classCount[vote] = 0
classCount[vote] += 1 # 儲存了 classList 中每個類標籤出現的頻率
sortedClassCount = sorted(classCount.iteritems(),\
key = operator.itemgetter(1), reverse = True) # 操作兼職排序字典
return sortedClassCount[0][0] # 返回出現次數最多的分類名稱# 建立樹的函式程式碼
def createTree(dataSet, labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList): # 類別完全相同則停止繼續劃分
return classList[0]
if len(dataSet[0]) == 1: # 遍歷完所有特徵時返回出現次數最多的
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet] # 得到列表包含的所有屬性值
uniqueVals = set(featValues)
for value in uniqueVals:
# 為了保證每次呼叫函式 createTree() 時不改變原始列表型別,使用新變數 subLabels 代替原始列表
subLabels = labels[:] # 這行程式碼複製了類標籤,並將其儲存在新列表變數 subLabels 中
myTree[bestFeatLabel][value] = createTree(splitDataSet\
(dataSet,bestFeat,value),subLabels)
return myTree下一步開始建立樹,使用 字典 型別來儲存樹的資訊,當然也可以宣告特殊的資料型別儲存樹,但是這裡沒有必要。
當前資料集選取的最好特徵儲存在變數 bestFeat 中,得到列表包含的所有屬性值。
現在執行程式碼,在 run_trees.py 裡面新增:
print '*********************************'
reload(trees)
print '>>> myDat, labels = trees.createDataSet()'
myDat, labels = trees.createDataSet()
print '>>> myTree = trees. createTree(myDat, labels)'
myTree = trees. createTree(myDat, labels)
print '>>> myTree'
print myTree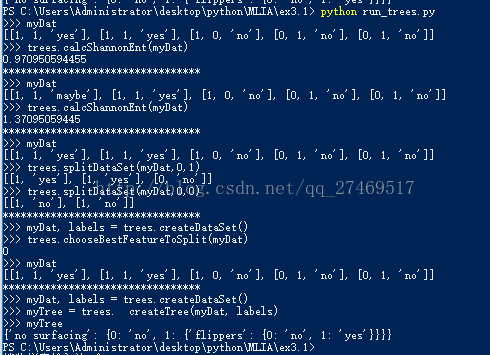
變數 myTree 包含了很多代表樹結構資訊的巢狀字典。