[JZOJ3395]【NOIP2013模擬】Freda的傳呼機
Description
為了 隨時 與 rainbow快速交流, Freda製造了 兩部傳呼機 。Freda和 rainbow所在的地方有N座房屋、M條雙向 光纜 。每條光纜連線兩座房屋, 傳呼機發出的訊號只能沿著光纜傳遞,並且 傳呼機的訊號 從光纜的其中一端傳遞到另需要花費 t單位時間 。現在 Freda要 進行 Q次試驗, 每次選取兩座房屋,並想知道 傳呼機的訊號在這兩座房屋之間傳遞 至少需 要多長時間。 Freda 和 rainbow簡直弱爆了有木有T_TT_T ,請你幫他們吧……
N座房屋 通過光纜 一定是連通的, 並且這 M條光纜有以下三類連線情況:
A:光纜不形成環 ,也就是光纜僅 有 N-1條。
B:光纜只 形成一個環,也就是光纜 僅有 N條。
C:每條光纜僅在一個環中。
Solution
宣告一下ABC類資料的多少
送分資料佔10%,2<=N<=1000,N-1<=M<=1200。
A類資料佔30%,M=N-1。
B類資料佔50%,M=N。
C類資料佔10%,M>N。
對於100%的資料,2<=N<=10000,N-1<=M<=12000,Q=10000,1<=x,y<=N,1<=t<=32768。
送分資料——直接
- A類資料——樹
- B類資料——環套樹
- C類資料——仙人掌
仙人掌就是許多個環由鏈串在一起,每條邊至多在一個環中。
先考慮A類
顯然直接
B類環套樹
環太噁心,我們考慮刪邊
你可以先用一個DFS把環搞出來,隨便找一條必定在環上的邊打上標記不能走
然後像樹一樣搞一遍,算最後答案的時候要取在樹上的答案和強制走這條邊的最小值。
關鍵在C類(話說只有10分啊!!棟爺:然而10分讓你無法AC~~)
首先我們從根開始跑一遍
現在我們需要把仙人掌弄成一個類似樹的東西。
我們將從根
設
設已走過的那個點是
如果
如果
我們需要記錄一個
知道這個環的環頂以後,我們可以把每個點都與環頂連一條邊,然後把環上其他邊都刪掉(也可以在剛剛的過程中順便做)
這樣,我們得到了一棵樹,暫且稱為仙人掌樹
然後再來一個
現在考慮求解。
對於兩個點
若
若
這時候剛才求得
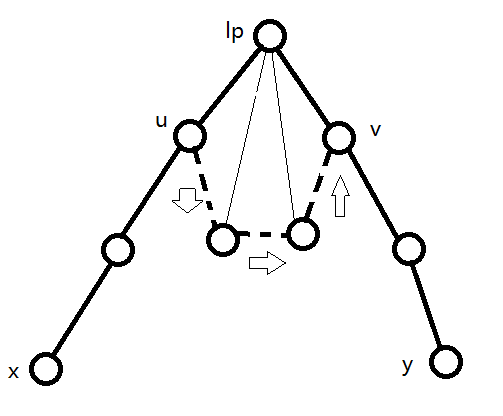
先上圖
假設
那麼
取個
Code
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cmath>
#define fo(i,a,b) for(i=a;i<=b;i++)
#define fod(i,a,b) for(i=a;i>=b;i--)
using namespace std;
struct note
{
int x,y,z,f,b;
};
bool cmp(note x,note y)
{
return x.x<y.x;
}
int n,m,q,a1[200005][2],delt,num;
note a[100000];
int dis[100005],d[100005],ft[100005][15],deep[200005],hf[200005],fx[100005],lg[200005],from[100005];
bool bz[100005],b1;
void spfa(int l)
{
int i,j,now;
memset(bz,0,sizeof(bz));
i=0;
j=1;
d[1]=l;
bz[l]=1;
dis[l]=0;
while (i<j)
{
i++;
int k;
now=d[i];
if (a1[now][0]>0)
fo(k,a1[now][0],a1[now][1])
{
int p=a[k].y;
if (dis[p]>dis[now]+a[k].z)
{
dis[p]=dis[now]+a[k].z;
if (bz[p]==0)
{
d[++j]=p;
bz[p]=1;
}
}
}
bz[now]=0;
}
}
void back(int k,int f)
{
if (k!=delt)
{
d[k]=d[a[f].y]+a[f].z;
a[f].b=1;
if (a[from[k]].x!=delt)
{
m++;
a[2*m-1].x=a[2*m].y=delt;
a[2*m-1].y=a[2*m].x=k;
a[2*m-1].f=a[2*m].f=m;
a[2*m-1].b=a[2*m].b=0;
}
hf[k]=num;
lg[num]+=a[f].z;
back(a[from[k]].x,from[k]);
}
else
{
lg[num]+=a[f].z;
delt=0;
}
}
void findh(int k,int f,int dep)
{
int i;
deep[k]=dep;
from[k]=f;
fo(i,a1[k][0],a1[k][1])
{
int p=a[i].y;
if (a[i].f!=a[f].f)
{
if(deep[p]==0)
{
findh(p,i,dep+1);
}
else if (deep[k]>deep[p])
{
delt=p;
hf[k]=++num;
d[k]=a[i].z;
lg[num]+=a[i].z;
back(a[f].x,f);
}
}
}
}
void dfs(int k,int f,int dep)
{
ft[k][0]=f;
deep[k]=dep;
int i;
fo(i,a1[k][0],a1[k][1])
{
int p=a[i].y;
if (p!=f&&a[i].b==0&&a[a[i].f].b==0)
{
dfs(p,k,dep+1);
}
}
}
int lca(int x,int y,int &u,int &v)
{
if (deep[x]<deep[y]) swap(x,y);
while(deep[x]!=deep[y])
{
int i=0;
while(deep[ft[x][i]]>deep[y]) i++;
if (i==0)
{
if (ft[x][0]==y)
{
u=v=x;
return ft[x][0];
}
x=ft[x][0];
break;
}
x=ft[x][--i];
}
while (x!=y)
{
int i=0;
while (ft[x][i]!=ft[y][i]) i++;
if (i==0)
{
u=x;
v=y;
return ft[x][0];
}
x=ft[x][--i];
y=ft[y][i];
}
}
int main()
{
freopen("call.in","r",stdin);
freopen("call.out","w",stdout);
cin>>n>>m>>q;
int i,j;
fo(i,1,m)
{
scanf("%d%d%d",&a[2*i-1].x,&a[2*i-1].y,&a[2*i-1].z);
a[2*i].x=a[2*i-1].y;
a[2*i].y=a[2*i-1].x;
a[2*i].z=a[2*i-1].z;
a[2*i].f=a[2*i-1].f=i;
a[2*i].b=a[2*i-1].b=0;
}
sort(a+1,a+2*m+1,cmp);
fo(i,1,2*m)
{
if (a[i].x!=a[i-1].x)
{
a1[a[i].x][0]=i;
a1[a[i-1].x][1]=i-1;
}
}
a1[a[2*m].x][1]=2*m;
memset(dis,107,sizeof(dis));
bz[1]=1;
spfa(1);
num=0;
delt=0;
findh(1,0,1);
sort(a+1,a+2*m+1,cmp);
fo(i,1,2*m)
{
if (a[i].x!=a[i-1].x)
{
a1[a[i].x][0]=i;
a1[a[i-1].x][1]=i-1;
}
if (fx[a[i].f]==0) fx[a[i].f]=i;
else
{
a[fx[a[i].f]].f=i;
a[i].f=fx[a[i].f];
}
}
a1[a[2*m].x][1]=2*m;
memset(deep,0,sizeof(deep));
dfs(1,0,1);
fo(i,1,trunc(log(n)/log(2)))
fo(j,1,n) ft[j][i]=ft[ft[j][i-1]][i-1];
fo(i,1,q)
{
int x,y,u,v;
scanf("%d%d",&x,&y);
if (x==y)
{
printf("0\n");
continue;
}
int lp=lca(x,y,u,v);
if (hf[u]!=hf[v]||hf[u]==0||hf[v]==0) printf("%d\n",dis[x]+dis[y]-2*dis[lp]);
else
{
if (u==v) printf("%d\n",abs(dis[x]-dis[y]));
else
{
int dx=dis[x]-dis[u],dy=dis[y]-dis[v],duv=abs(d[u]-d[v]);
printf("%d\n",min(duv,lg[hf[u]]-duv)+dx+dy);
}
}
}
}