徹底理解數字影象處理中的卷積-以Sobel運算元為例
連結: 原文出處
作者: FreeBlues
概述
卷積在訊號處理領域有極其廣泛的應用, 也有嚴格的物理和數學定義. 本文只討論卷積在數字影象處理中的應用.
在數字影象處理中, 有一種基本的處理方法:線性濾波. 待處理的平面數字影象可被看做一個大矩陣, 影象的每個畫素對應著矩陣的每個元素, 假設我們平面的解析度是 1024*768, 那麼對應的大矩陣的行數= 1024, 列數=768.
用於濾波的是一個濾波器小矩陣(也叫卷積核), 濾波器小矩陣一般是個方陣, 也就是 行數 和 列數 相同, 比如常見的用於邊緣檢測的 Sobel 運算元 就是兩個 3*3 的小矩陣.
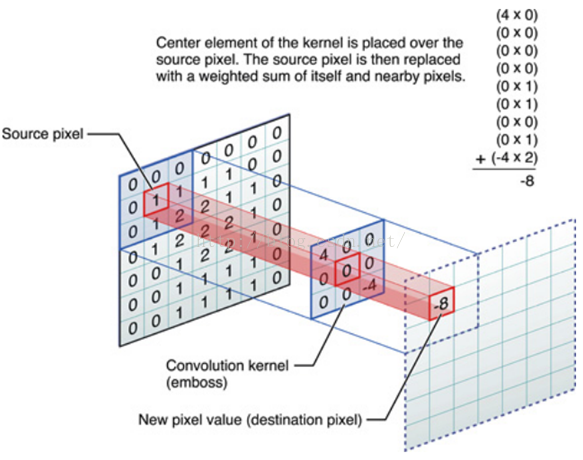
進行濾波就是對於大矩陣中的每個畫素, 計算它周圍畫素和濾波器矩陣對應位置元素的乘積, 然後把結果相加到一起, 最終得到的值就作為該畫素的新值, 這樣就完成了一次濾波
影象卷積計算示意圖:
對影象大矩陣和濾波小矩陣對應位置元素相乘再求和的操作就叫卷積(Convolution)或協相關(Correlation).
協相關(Correlation)和卷積(Convolution)很類似, 兩者唯一的差別就是卷積在計算前需要翻轉卷積核, 而協相關則不需要翻轉.
以 Sobel 運算元為例
Sobel 運算元 也叫 Sobel 濾波, 是兩個 3*3 的矩陣, 主要用來計算影象中某一點在橫向/縱向上的梯度, 看了不少網路上講解 Sobel 運算元 的文章, 發現人們常常把它的橫向梯度矩陣和縱向梯度矩陣混淆. 這可能與 Sobel 運算元 在它的兩個主要應用場景中的不同用法有關.
Sobel 運算元的兩個梯度矩陣: Gx 和 Gy
這裡以 Wiki 資料為準, Sobel 運算元 有兩個濾波矩陣: Gx 和 Gy, Gx 用來計算橫向的梯度, Gy 用來計算縱向的梯度, 下圖就是具體的濾波器:
注意:這裡列出的這兩個梯度矩陣對應於橫向從左到右, 縱向從上到下的座標軸, 也就是這種:
原點
O ——-> x軸
|
|
|
V y軸
Sobel 運算元的用途
它可以用來對影象進行邊緣檢測, 或者用來計算某個畫素點的法線向量. 這裡需要注意的是:
- 邊緣檢測時: Gx 用於檢測縱向邊緣, Gy 用於檢測橫向邊緣.
- 計演算法線時: Gx 用於計演算法線的橫向偏移, Gy用於計演算法線的縱向偏移.
計算展開
假設待處理影象的某個畫素點周圍的畫素如下:
| 左上畫素 | 上邊畫素 | 右上畫素 |
|---|---|---|
| 左邊畫素 | 中心畫素 | 右邊畫素 |
| 坐下畫素 | 下邊畫素 | 右下畫素 |
那麼用 Gx 計算展開為:
橫向新值 = (-1) x [左上] + (-2) x [左] + (-1) x [左下] + 1 x [右上] + 2 x [右] + 1 x [右下]
用 Gy 計算展開為:
縱向新值 = (-1) x [左上] + (-2) x [上] + (-1) x [右] + 1 x [左下] + 2 x [下] + 1 x [右下]
前面說過, 做影象卷積時需要翻轉卷積核, 但是我們上面的計算過程沒有顯式翻轉, 這是因為 Sobel 運算元 繞中心元素旋轉 180 度後跟原來一樣. 不過有些 卷積核 翻轉後就變了, 下面我們詳細說明如何翻轉卷積核.
卷積核翻轉
前面說過, 影象卷積計算, 需要先翻轉卷積核, 也就是繞卷積核中心旋轉 180度, 也可以分別沿兩條對角線翻轉兩次, 還可以同時翻轉行和列, 這3種處理都可以得到同樣的結果.
對於第一種卷積核翻轉方法, 一個簡單的演示方法是把卷積核寫在一張紙上, 用筆尖固定住中心元素, 旋轉 180 度, 就看到翻轉後的卷積核了.
下面演示後兩種翻轉方法, 示例如下:
假設原始卷積核為:
| a | b | c |
|---|---|---|
| d | e | f |
| g | h | i |
方法2:沿兩條對角線分別翻轉兩次
先沿左下角到右上角的對角線翻轉, 也就是 a和i, b和f, d和h交換位置, 結果為:
| i | f | c |
|---|---|---|
| h | e | b |
| g | d | a |
再沿左上角到右下角的對角線翻轉, 最終用於計算的卷積核為:
| i | h | g |
|---|---|---|
| f | e | d |
| c | b | a |
方法3:同時翻轉行和列
在 Wiki 中對這種翻轉的描述:
convolution is the process of flipping both the rows and columns of the kernel and then multiplying locationally similar entries and summing.
也是把卷積核的行列同時翻轉, 我們可以先翻轉行, 把 a b c跟 g h i 互換位置, 結果為:
| g | h | i |
|---|---|---|
| d | e | f |
| a | b | c |
再翻轉列, 把 g d a 和 i f c 互換位置, 結果為:
| i | h | g |
|---|---|---|
| f | e | d |
| c | b | a |
在 Wiki 中有一個計算展開式, 也說明了這種翻轉:
注意:這裡要跟矩陣乘法區分開, 這裡只是借用了矩陣符號, 實際做的是對應項相乘, 再求和.
影象邊緣畫素的處理
以上都預設待處理的畫素點周圍都有畫素, 但是實際上影象邊緣的畫素點周圍的畫素就不完整, 比如頂部的畫素在它上方就沒有畫素點了, 而影象的四個角的畫素點的相鄰畫素更少, 我們以一個影象矩陣為例:
| 左上角 | … | … | 右上角 |
|---|---|---|---|
| … | … | … | … |
| 左側 | … | … | … |
| … | … | … | … |
| 左下角 | … | … | 右下角 |
位於左上角的畫素點的周圍就只有右側和下方有相鄰畫素, 遇到這種情況, 就需要補全它所缺少的相鄰畫素, 具體補全方法請參考下一節的程式碼.
用GPU進行影象卷積
如果在 CPU 上實現影象卷積演算法需要進行4重迴圈, 效率比較差, 所以我們試著把這些卷積計算放到 GPU 上, 用 shader 實現, 結果發現效能相當好, 而且因為頂點著色器和片段著色器 本質就是一個迴圈結構, 我們甚至不需要顯式的迴圈, 程式碼也清晰了很多.
影象卷積在程式碼中的實際應用, 下面是一個 GLSL 形式的著色器, 它可以根據紋理貼圖生成對應的法線圖:
// 用 sobel 運算元生成法線圖 generate normal map with sobel operator
genNormal1 = {
vertexShader = [[
attribute vec4 position;
attribute vec4 color;
attribute vec2 texCoord;
varying vec2 vTexCoord;
varying vec4 vColor;
varying vec4 vPosition;
uniform mat4 modelViewProjection;
void main()
{
vColor = color;
vTexCoord = texCoord;
vPosition = position;
gl_Position = modelViewProjection * position;
}
]],
fragmentShader = [[
precision highp float;
varying vec2 vTexCoord;
varying vec4 vColor;
varying vec4 vPosition;
// 紋理貼圖
uniform sampler2D tex;
uniform sampler2D texture;
//影象橫向長度-寬度, 影象縱向長度-高度
uniform float w;
uniform float h;
float clamp1(float, float);
float intensity(vec4);
float clamp1(float pX, float pMax) {
if (pX > pMax)
return pMax;
else if (pX < 0.0)
return 0.0;
else
return pX;
}
float intensity(vec4 col) {
// 計算畫素點的灰度值
return 0.3*col.x + 0.59*col.y + 0.11*col.z;
}
void main() {
// 橫向步長-每畫素點寬度,縱向步長-每畫素點高度
float ws = 1.0/w ;
float hs = 1.0/h ;
float c[10];
vec2 p = vTexCoord;
lowp vec4 col = texture2D( texture, p );
// sobel operator
// position. Gx. Gy
// 1 2 3 |-1. 0. 1.| |-1. -2. -1.|
// 4 5 6 |-2. 0. 2.| | 0. 0. 0.|
// 7 8 9 |-1. 0. 1.| | 1. 2. 1.|
// 右上角,右,右下角
c[3] = intensity(texture2D( texture, vec2(clamp(p.x+ws,0.,w), clamp(p.y+hs,0.,h) )));
c[6] = intensity(texture2D( texture, vec2(clamp1(p.x+ws,w), clamp1(p.y,h))));
c[9] = intensity(texture2D( texture, vec2(clamp1(p.x+ws,w), clamp1(p.y-hs,h))));
// 上, 下
c[2] = intensity(texture2D( texture, vec2(clamp1(p.x,w), clamp1(p.y+hs,h))));
c[8] = intensity(texture2D( texture, vec2(clamp1(p.x,w), clamp1(p.y-hs,h))));
// 左上角, 左, 左下角
c[1] = intensity(texture2D( texture, vec2(clamp1(p.x-ws,w), clamp1(p.y+hs,h))));
c[4] = intensity(texture2D( texture, vec2(clamp1(p.x-ws,w), clamp1(p.y,h))));
c[7] = intensity(texture2D( texture, vec2(clamp1(p.x-ws,w), clamp1(p.y-hs,h))));
// 先進行 sobel 濾波, 再把範圍從 [-1,1] 調整到 [0,1]
// 注意: 比較方向要跟座標軸方向一致, 橫向從左到右, 縱向從下到上
float dx = (c[3]+2.*c[6]+c[9]-(c[1]+2.*c[4]+c[7]) + 1.0) / 2.0;
float dy = (c[7]+2.*c[8]+c[9]-(c[1]+2.*c[2]+c[3]) + 1.0) / 2.0;
float dz = (1.0 + 1.0) / 2.0;
gl_FragColor = vec4(vec3(dx,dy,dz), col.a);
}
]]
}