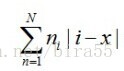原題目如下：

亞洲微軟研究院所在的希格瑪大廈一共有6部電梯。在高峰時間，每層都有人上下，電梯每層都停。實習生小飛常常會被每層都停的電梯弄的很不耐煩，於是他提出了這樣一個辦法：

由於樓層並不算太高，那麼在繁忙的上下班時間，每次電梯從一層往上走時，我們只允許電梯停在其中的某一層。所有乘客從一樓上電梯，到達某層後，電梯停下來，所有乘客再從這裡爬樓梯到自己的目的層。在一樓的時候，每個乘客選擇自己的目的層，電梯則計算出應停的樓層。
問：電梯停在哪一層樓，能夠保證這次乘坐電梯的所有乘客爬樓梯的層數之和最少？

解法一：從第一層到第N層全部算一遍，記錄最小值和停留層。一般人最先想到的辦法都是這樣，但追求效率的人肯定會想別的辦法，從而有第二種解法

解法二：假設電梯停在第i層，我們可以先計算所有乘客總共要爬的層數Y，如果有N1個乘客在i層以下，有N2個乘客在i層，N3個乘客在i層以上。這個時候如果電梯改停i-1層，則所有目的地在第i層及以上的乘客都要多爬一層，總共需要多爬N2+N3層，而所有i-1及以下的乘客都可以少爬一層，總共少爬N1層，因此乘客總共需要爬的層數為Y-N1+N2+N3 = Y - (N1 - N2 - N3);反之如果改停在i+1層時，則總共需要爬的層數為 Y + (N1 + N2 - N3)。由此可見當N1 > N2 + N3時，停i-1層比停i層好，而當N1+N2<N3時，停i+1比停i層要好，否則，停i層最好。這個演算法可以一次迴圈算出最優解。

解法三：這是我一個朋友給的演算法，假設停在x層，ni為第i層的人數，則總共需要爬的層數為

所以使上式取得最小值的x就是題目的解，解法如下

這樣我們也可以在一次遍歷內，利用SN - 2SK<0找出題目的解

說明：我曾想過用方差的思想來求這個問題，這樣就可以消除絕對值符號了，通過求導或展開式子化成對稱軸方程形式來求解，但這種方法求得的解並不一定是正確解，它有正負1的誤差，還不清楚為什麼