先以一個簡單直觀的例項來介紹k-d樹演算法。假設有6個二維資料點{（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}，資料點位於二維空間內（如圖2中黑點所示）。k-d樹演算法就是要確定圖2中這些分割空間的分割線（多維空間即為分割平面，一般為超平面）。下面就要通過一步步展示k-d樹是如何確定這些分割線的。

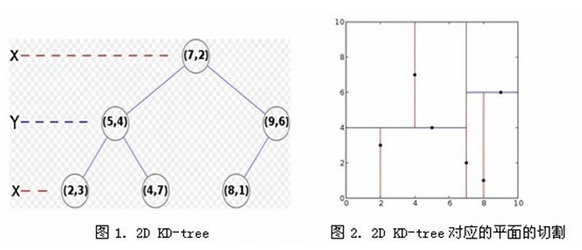
k-d樹演算法可以分為兩大部分，一部分是有關k-d樹本身這種資料結構建立的演算法，另一部分是在建立的k-d樹上如何進行最鄰近查詢的演算法。

構造kd樹

kd樹是一種對k維空間中的例項點進行儲存以便對其進行快速搜尋的樹形資料結構。kd樹是二叉樹，表示對k維空間的一個劃分。構造kd樹相當於不斷地用垂直於座標軸的超平面將k維空間進行切分，構成一系列的k維超矩形區域。kd樹的每一個節點對應於一個k維超矩形區域。k-d樹是一個二叉樹，每個節點表示一個空間範圍。

由於此例簡單，資料維度只有2維，所以可以簡單地給x，y兩個方向軸編號為0,1，也即split={0,1}。
（1）確定split域的首先該取的值。分別計算x，y方向上資料的方差得知x方向上的方差最大，所以split域值首先取0，也就是x軸方向；
（2）確定Node-data的域值。根據x軸方向的值2,5,9,4,8,7排序選出中值為7，所以Node-data = （7,2）。這樣，該節點的分割超平面就是通過（7,2）並垂直於split = 0（x軸）的直線x = 7；
（3）確定左子空間和右子空間。分割超平面x = 7將整個空間分為兩部分，如下圖所示。x <= 7的部分為左子空間，包含3個節點{（2,3），（5,4），（4,7）}；另一部分為右子空間，包含2個節點{（9,6），（8,1）}。

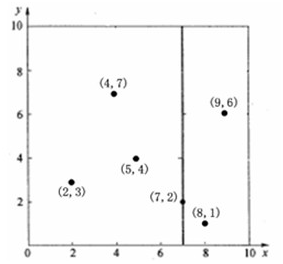
如演算法所述，k-d樹的構建是一個遞迴的過程。然後對左子空間和右子空間內的資料重複根節點的過程就可以得到下一級子節點（5,4）和（9,6）（也就是左右子空間的'根'節點），同時將空間和資料集進一步細分。如此反覆直到空間中只包含一個數據點，如下圖所示。最後生成的k-d樹如下圖所示。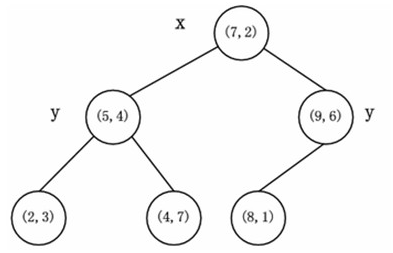

搜尋kd樹

在k-d樹中進行資料的查詢也是特徵匹配的重要環節，其目的是檢索在k-d樹中與查詢點距離最近的資料點。這裡先以一個簡單的例項來描述最鄰近查詢的基本思路。
星號表示要查詢的點（2.1,3.1）。通過二叉搜尋，順著搜尋路徑很快就能找到最鄰近的近似點，也就是葉子節點（2,3）。而找到的葉子節點並不一定就是最鄰近的，最鄰近肯定距離查詢點更近，應該位於以查詢點為圓心且通過葉子節點的圓域內。為了找到真正的最近鄰，還需要進行'回溯'操作：演算法沿搜尋路徑反向查詢是否有距離查詢點更近的資料點。此例中先從（7,2）點開始進行二叉查詢，然後到達（5,4），最後到達（2,3），此時搜尋路徑中的節點為小於（7,2）和（5,4），大於（2,3），首先以（2,3）作為當前最近鄰點，計算其到查詢點（2.1,3.1）的距離為0.1414，然後回溯到其父節點（5,4），並判斷在該父節點的其他子節點空間中是否有距離查詢點更近的資料點。以（2.1,3.1）為圓心，以0.1414為半徑畫圓，如下圖所示。發現該圓並不和超平面y = 4交割，因此不用進入（5,4）節點右子空間中去搜索。

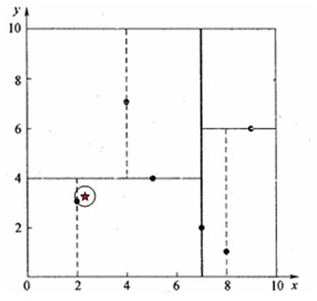
再回溯到（7,2），以（2.1,3.1）為圓心，以0.1414為半徑的圓更不會與x = 7超平面交割，因此不用進入（7,2）右子空間進行查詢。至此，搜尋路徑中的節點已經全部回溯完，結束整個搜尋，返回最近鄰點（2,3），最近距離為0.1414。
一個複雜點了例子如查詢點為（2，4.5）。同樣先進行二叉查詢，先從（7,2）查詢到（5,4）節點，在進行查詢時是由y = 4為分割超平面的，由於查詢點為y值為4.5，因此進入右子空間查詢到（4,7），形成搜尋路徑<（7,2），（5,4），（4,7）>，取（4,7）為當前最近鄰點，計算其與目標查詢點的距離為3.202。然後回溯到（5,4），計算其與查詢點之間的距離為3.041。以（2，4.5）為圓心，以3.041為半徑作圓，如下圖左所示。可見該圓和y = 4超平面交割，所以需要進入（5,4）左子空間進行查詢。此時需將（2,3）節點加入搜尋路徑中得<（7,2），（2,3）>。回溯至（2,3）葉子節點，（2,3）距離（2,4.5）比（5,4）要近，所以最近鄰點更新為（2，3），最近距離更新為1.5。回溯至（7,2），以（2,4.5）為圓心1.5為半徑作圓，並不和x = 7分割超平面交割，如下圖右所示。至此，搜尋路徑回溯完。返回最近鄰點（2,3），最近距離1.5。

經典的構造k-d tree的規則如下：

1. 隨著樹的深度增加，迴圈的選取座標軸，作為分割超平面的法向量。對於3-d tree來說，根節點選取x軸，根節點的孩子選取y軸，根節點的孫子選取z軸，根節點的曾孫子選取x軸，這樣迴圈下去。
2. 每次均為所有對應例項的中位數的例項作為切分點，切分點作為父節點，左右兩側為劃分的作為左右兩子樹。